Nour-Eddine and Abdelkader: GMM-Based Maghreb Dialect Identification System
Abstract
While Modern Standard Arabic is the formal spoken and written language of the Arab world; dialects are the major communication mode for everyday life. Therefore, identifying a speaker’s dialect is critical in the Arabic-speaking world for speech processing tasks, such as automatic speech recognition or identification. In this paper, we examine two approaches that reduce the Universal Background Model (UBM) in the automatic dialect identification system across the five following Arabic Maghreb dialects: Moroccan, Tunisian, and 3 dialects of the western (Oranian), central (Algiersian), and eastern (Constantinian) regions of Algeria. We applied our approaches to the Maghreb dialect detection domain that contains a collection of 10-second utterances and we compared the performance precision gained against the dialect samples from a baseline GMM-UBM system and the ones from our own improved GMM-UBM system that uses a Reduced UBM algorithm. Our experiments show that our approaches significantly improve identification performance over purely acoustic features with an identification rate of 80.49%.
Key words: Core-Set, Gaussian Mixture Models (GMM), Kernel Methods, Minimal Enclosing Ball (MEB), Quadratic Programming (QP), Support Vector Machines (SVMs), Universal Background Model (UBM)
1. Introduction
One of the key challenges in Arabic speech research is to find the differences between Arabic dialects. Most of the recent works on Arabic speech have addressed the problem of identifying or recognizing Modern Standard Arabic. A few studies have focused on Arabic dialects [ 1, 2], but no research has been carried out for the west Arabic countries (Maghreb). Arabic Maghreb dialects differ from Modern Standard Arabic and each other in many dimensions of the linguistic spectrum, as well as morphologically, lexically, syntactically, and phonologically. One of the guiding questions we used for our research was, can a speaker’s regional origin or regional dialect within a given language group be determined for a given small sample of his or her speech? Our aim was to identify the dialect of a speaker from among the following five Maghrebian ones: Moroccan, Tunisian, and three Algerian dialects of Oranian, Algiersian, and Constantinian.
Since speakers with different dialects often pronounce some words differently and consistently alter certain phonemes, identifying the regional dialect prior to automatic speech identification allows to use more restricted pronunciation dictionary in decoding, which results will be in a reduced search space with a lower perplexity. However, no work in the speech topic literature has addressed the issues that are related to Maghrebian dialects.
To handle this problem, we improved an UBM-GMM identification system by reducing the Universal Background Model (UBM) of the system by using two approaches based on Support Vector Machines (SVMs) that were reduced to Minimal Enclosing Ball (MEB) problems [ 3] using the fuzzy Cmean clustering method. The core idea of these two approaches is to adopt multi-class SVMs formulation and MEB formulation to reduce the size of the dataset by eliminating data out of the ball defined in the MEB. We extracted Mel-Frequency Cepstral Coefficients (MFCCs) features from our own corpus (cf. Section 2) and then computed Shifted-Delta Cepstral (SDC) coefficients to identify the dialect of a regional speaker. We conducted a series of experiments to test our approach on spontaneous conversations in five different Arabic Maghreb dialects. We then compared the accuracy of the results of our improved UBM-GMM identification system to a baseline UBM-GMM identification system.
In this paper we defined the variables t, n, m, as follows:
t: index of frame, T : number of frames. n: index of feature dimension, N: dimensionality of feature. m: index of Gaussian component, M: number of Gaussian components.
The remainder of the paper is organized as follows: in the next three sections, we give some preliminaries where a review of the relevant research streams is provided. Then, Sections 2–4 are devoted to present the Maghrebian corpus, the Gaussian Mixture Model (GMM), and UBM MAP adaptation. Two approaches to reduce data based on MEBs are described in Section 5. In Section 6, we present our proposal of a dialect identification system based on UBM-GMM. In Section 7, we report on some of the empirical experiments that we conducted on our proper database. Finally, in Section 8, we give the conclusion, which summarizes the contributions of this work and outlines potential research opportunities in the realm of Maghreb dialects identification.
2. Maghreb Dialect Corpus
Maghreb refers to the Arabic geographical region, which includes Morocco, Tunisia, Algeria, and Western Libya. The Maghreb dialects are the languages that are spoken in the aforementioned countries, and relabeled by the majority of their speakers as Darija, meaning ‘dialect’. Since, France and Spain colonized the Maghreb region, the dialects of the latter combine many French and Spanish words with Arabic suffixes to form words. This form of Arabic is not written and is less static, as it changes frequently. The Maghreb dialects’ phonemes differ in that speakers make no distinction between short and long vowels.
When training a system to identify dialects, it is important to use training and testing corpora under similar acoustic conditions. However, for our study, we used our own corpus of spontaneous speech issues from movies and TV shows, for which acoustic conditions are not similar to native artists’ speakers of the Arabic Maghreb Dialects. The corpus was made up of Moroccan, Tunisian, and three Algerian dialects (Oranian, Algiersian, and Constantinian). We used speech from:
92 speakers (54.19 h) of the Moroccan conversational artists, holding out 25 speakers for testing. 98 speakers (49.73 h) from the Oranian conversational artists, holding out 40 speakers for testing. 125 speakers (51.32 h) from the Algiersian conversational artists, holding out 32 speakers for testing. 80 speakers (45.18 h) from the Constantinian conversational artists, holding out 21 speakers for testing. 130 speakers (53.73 h) from the Tunisian conversational artists, holding out 43 speakers for testing.
3. Gaussian Mixture Model
GMMs are widely used in many speech identification and recognition applications. They provide a convenient means of modeling complex probability distributions by representing the probability density function of a random variable with a sum of weighted Gaussians. We give a brief outline of the equations that we used to form our models [ 4]. A GMM is a type of density model that represents a dialect or language model. It defines many different Gaussian distributions where each of them has its mean, variance, and weight in the GMM models. Suppose that M is the number of small Gaussian distributions to model. The GMM, the following equation attempts to model the probability density of a N-dimensional random vector x, by adding weighted combination of multivariate Gaussian densities:
by:
where wm represents the Gaussian mixture weights, μm represents the mean, and ∑m represents the diagonal covariance matrices with
Σm=1M wm=1.
The GMM is defined by the mixing of all components that represent the mean vector, covariance matrix, and weight for each model, as described below:
In a GMM-based dialect identification system, each dialect identified is modeled by mth order GMM parameter parameter λd = {wm,μm,∑m} m = 1,…, M. The model parameters λd for dialect d are estimated with an Expectation-Maximization (EM) algorithm by the spectral features
X={xt}t=1T, which are extracted from a collection of speech utterances spoken in a dialect d.
GMM parameters are defined by using maximum likelihood training estimation, such as:
EM algorithm estimates maximum likelihood parameters. The basic idea is first based on initializing the model and then on estimating the model using a function such that the new model represents better parameters. After each dialect training, we obtained the mean, covariance, and weight of each Gaussian component. The algorithm consists of two main steps: the expectation E-step and the maximization M-step. The E-step set of parameters are calculated using the current complete data likelihood function of the expected value, while the M-step is carried out by maximizing the expected function to get the new parameters. The E-step and M-step follow an iterative process until convergence.
First, we defined Q as:
where, m is the number of Gaussian component, λm is the current model parameter, and λ̄m is the new parameter.
EM Algorithm
|
E-step: calculate p(x|λm) where
x={xt}t=1T
|
|
M-step: maximise Q function, and solve the Q(λm, λ̂m) coresponding to
{wm,μm,Σm}m=1M, then |
|
|
During the identification step, an unknown speech utterance X, is classified following the average log likelihood calculation produced by the dialect model, which is given by:
The maximum-likelihood classifier hypothesis H is calculated as:
Generally, GMMs do not tend to capture temporal dependencies satisfactorily. Hence, the introduction of Shifted Delta Coefficient that represents the acoustic features allows an acceptable performance [ 5]. The excellent language identification performances [ 6, 7] establish the GMMs as a major language identification approach.
4. UBM MAP Adaptation
The EM algorithm estimates the UBM and dialect model in a similar way. However, to reduce computation and to improve performance when only a limited number of training utterances are available, we propose the use of a Bayesian maximum a posteriori (MAP) adaptation. The MAP principle [ 8] differs from maximum likelihood as it assumes the parameters λd of the distribution p( X| λd) such that a random variable has a prior distribution p( λd). The MAP principle states that we should select λ̂d, where the posterior probability density of the latter is maximized, as: Using MAP for dialect model adaptation usually means that the prior distribution for the dialect model parameters is represented by the world model parameters [ 9]. Moreover, by using a global parameter to tune the relative importance of the prior distribution we can further do simplification without having a loss in performance. Based on the posterior probability of Gaussian m, we calculate ŵm, μ̂m, and Σ̂ m which are the new weights, means, and diagonal covariance matrices that correspond, respectively, to the weights, means, and diagonal covariance matrices in the world model. The posterior probability is defined as follows:
Adaptation, for all parameters of Gaussian m, is done as follows:
For each mixture and each parameter, a data dependent adaptation coefficient α is used in the above equations and is defined as:
where r, is a fixed relevance factor.
5. Reducing Data Based on MEBs
This section presents two approaches based on L2-SVMs that have been reduced to MEB problems [ 3] using the fuzzy C-mean clustering method. The algorithms for computing L2-SVMs based on the MEB equivalence used the greedy computation of a Core-Set, which is a typically small data subset that provides the same MEB as the full dataset. Therefore, we formulated a new multi-class SVM problem using Core-Sets to reduce large datasets, which can optimally match the input demands of different background architectures of language or dialect identification systems. The core idea of these two approaches is to adopt a multi-class SVMs formulation and MEB in order to reduce dataset so that the data located far from the ball data that was defined in the Core-Set are eliminated.
5.1 L2-Support Vector Machines
Given a training data set
S=(X,Y)={(xt,yt)}t=1T where xt ∈ ℝ N and yt ∈{+1, −1}, SVMs address the problem of binary classification by building a hyperplane in a feature space
Z=φ(X)={zt=φ(xt)}t=1T that is implicitly induced from X by means of a kernel function k( xt, xt′), which computes the dot products
zt′zt′=φ(xt)′φ(xt′) in Z directly on X (cf. Fig. 1.(b)). The L2-SVM chooses the separating hyperplane f( z) by solving the following quadratic program: After introducing Lagrange multipliers, the problem to solve is equivalent to:
where,
Ktt′=ytyt′k(xt,xt′)+ytyt′+δtt′C, δtt′ is the Kronecker delta function and k(xt,xt′) implements the dot-product
zt′zt′.
The optimal value is determined using model selection techniques and depends on the degree of noise and overlap among the classes [ 10]. With respect to Karush-Kuhn-Tucker (KKT) conditions, the hyperplane parameters are recovered as
w=Σt=1T ytαtzt and
b=Σt=1T αtyt. Note that the solution finally depends only on the examples for αi ≠ 0, which are called the support vectors.
5.2 Minimal Enclosing Balls
In [ 11], it is shown that the main appeal of the L2-SVM implementation is that it supports a convenient reduction to a MEB problem when the kernel used in the SVM is normalized, that is, k( x, x)= κ ∀ x ∈ X where κ in which is a constant. The advantage of this equivalence is that the Badoiu and Clarkson algorithm [ 12] can efficiently approximate the solution of a MEB problem with any degree of accuracy. If the training data set is
S={z˜t}t=1T then let Z̃ a space be equipped with a dot product
z˜t′z˜t′ that corresponds to the norm || z̃|| 2 = z̃′ z̃. As such, we define the ball ℬ ( c, R) of the center c ∈ Z̃ and radius R in ℝ as the subset of points z̃ ∈ Z̃, for which || z̃– c|| 2 ≤ R2. The MEB [ 5] of a set of points S={ z̃t: t ∈ T} in Z̃ is in turn the ball ℬ *( S, c*, R*) of the smallest radius that contains S (cf Fig. 1(a)), that is, the solution to the following optimization problem is: After introducing Lagrange multipliers, we obtained the following dual problem, with respect to the optimality conditions, which is as follows:
if we consider that
Σt∈T αtz˜t′z˜t=κ is a constant, as supposed in the above L2-SVM formulation, we can drop it from the dual objective in Eq. (17) and obtain a simpler QP problem of: In [ 11], it is shown that the primal variables c and R can be recovered from the optimal α as:
c=Σt=1Tαtz˜t, R=Σt=1T Σt′=1T αtαt′z˜t′z˜t′.
5.3 Core-Set Definition
Badoiu and Clarkson [ 12] define the Core-Set of S as a set CS ⊂ S where the MEB computed over CS is equivalent to the MEB considering for all of points included in S. A ball ℬ( c, R) is said an ε- approximation to the MEB ℬ *( S, c*, R*) of S if R ≤ R* and it contains S up to precision ε, that is: S ⊂ ℬ ( c,(1+ ε) R). Consequently, a set CS,ε is called an ε- Core-Set if the MEB of CS,ε is an ε- approximation to ℬ *( S, c*, R*) (cf. Fig. 2). If we consider S to be a set of T points in ℝN, R and is the radius of MEB(S), then, there exists a subset CS ⊂ S such that:
-
➢ The center c(CS)MEB(CS) of satisfiesd (z,c(CS))≤(1+ε)R, ∀ z ∈ S, such that a subset CS is a Core-Set of S for MEB. Then, a Core-Set is a subset CS of S such that:
ε-Core-Set: The solution for CS is within ε of the solution for S.
Next we present the most usual version of the algorithm used in [ 12].
Algorithm 1
Bãdoiu-Clarkson Algorithm
|
1: |
Initialize the core-set CS,ε.
|
|
2: |
Compute the minimal-enclosing-ball ℬ (CS, c, R) of the core-set CS,ε.
|
|
3: |
while A point z̃ ∈ S out of the ball ℬ (C, c, (1+ε)R) exist do
|
|
4: |
Include z̃ in CS,ε.
|
|
5: |
Compute the minimal-enclosing-ball ℬ (CS, c, R) of the core-set CS,ε.
|
|
6: |
end while
|
In [ 12], it is proved that the algorithm of Bãdoiu and Clarkson is a greedy approach that is used to find a ε- Core-Set of S, which converges in no more than
O (1ɛ) iterations. Since each iteration adds only one point to the Core-Set, the final size of the Core-Set is also
O (1ɛ). Hence, the accuracy/complexity tradeoff of the obtained solution monotonically depends on ε.
5.4 Multi-Class Extensions
In a multi-class problem, the samples {xt} belong to a set of L categories c ∈{cl; l ∈ L} with L>2 and hence, the two ‘codes’ +1 and −1 used to denote the two sides of a separating hyperplane are no longer enough to implement a decision function.
There are two types of extensions to build multi-class SVMs [ 13, 14]. The first is the One-Versus-One (OVO) approach, which uses several binary classifiers that are separately trained and joined into a multi-category decision function. The second is the One-Versus-All (OVA) approach where a different binary SVM is used to separate each class from the all other classes. In [ 15], it is shown that multi-class extension of L2-SVMs preserves the data reduction to a MEB problem, which is the key requirement of our algorithms that improve the Maghreb dialects identification system, as detailed in the section below. Let the training dataset be
S={(xt,yt)}t=1T, where xt ∈ ℝN and yt ∈ ℝL for some integers. We have T training points whose labels are vector valued. For a given training task having L classes, these label vectors are chosen out of the defined set of vectors {y1, y2,…,yT}. Now, for the inputs z=φ(x), the primal objective function for the learning problem can be defined as:
Several selections are possible for the norm ||W||2. A common choice is the so-called Frobenius norm ||W||2 =trace(W′W). Hence, the dual of the optimization problem obtained after introducing Lagrange multipliers is:
where
Ktt′=yt′yt′k(xt,xt′)+yt′yt′+δtt′C, δtt′ is the Kronecker delta function and k(xt,xt′) implements the feature dot products
zt′zt′.
Hence, the primal solutions W, b, are obtained with respect to the Karush-Kuhn-Tucker (KKT) conditions on Eq. (22) as
W=Σt=1T αtytzt′ and
b=Σt=1T αtyt. Note that in this formulation, the selection of the codes used to represent the classes is arbitrary. The decision mechanism determines the code, which is more similar to the code recovered by the operator W that is arg
maxl=1,…,L yl′(W′z+b). So, the decision function predicting one of the labels from 1,..., L for any test zt is expressed as: Now, the arising question is about choosing the label vectors. We defined ytl ∈ ℝ from [ 16]. Let ytl denote the lth element of the label vector yt corresponding to zt. One of the convenient ways is to choose ytl as: Then the inner product between the vectors will be:
5.5 MEB and Multi-Class L2-SVMs Equivalence
Now the computation of the MEB is in feature space Z̃=φ(X), which has been induced from X by the mapping function φ: X → Z̃ where we can compute the dot products in Z̃ directly from X by using a kernel function
k˜(xt,xt′)=φ(xt)′φ(xt′)=z˜t′z˜t′. In addition, we suppose that the kernel is normalized, i.e., ∀ x ∈ X, k̃(x,x)=κ for example: with κ ∈ ℝ a constant.
As seen above, the optimization problem Eq. (17) is equivalent to solve the following quadratic program: where, K̃tt′ = k( xt, xt′). This problem coincides with the binary L2-SVM problem shown in Eq. (23) that was obtained from the dual objective in Eq. (18) and its multi-class implementation in Eq. (21). As seen above, for the binary case, we set
k˜(xt,xt′)=ytyt′k(xt,xt′)+ytyt′+δtt′C, while in the multi-category case, we set
k˜(xt,xt′)=yt′yt′k(xt,xt′)+yt′yt′+δtt′C. The key requirement of the latter equivalence is the normalization constraint on k̃( x, x)= κ.
5.6 Data Reduction Approaches
The key idea of our method is to cast a L2-SVM as a MEB problem that has been reduced in a Core-Set by using a feature space Z̃= φ( X), where the training examples are embedded through the mapping of φ. Hence, we first formulated an algorithm to compute the MEB of the images S̃ of S in Z̃ when S is decomposed in a collection of subsets Sp. Then, we instantiated the solution for classifiers supporting the reduction to MEB problems (cf. Fig. 3). Our proposed algorithm is based on the idea of computing Core-Sets
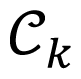 for each set S̃p = φ( Sp) and taking union of all the Core-Sets
 = ∪ p
 as an approximation to a Core-Set for S̃ = ∪ p Sp. Algorithm 2 depicts the generic procedure. In the first step, the algorithm extracts a Core-Set for each subset Sp. In the second step, the MEB of the union of the Core-Sets is computed. The decomposition of S in a collection of subsets Sp by the fuzzy C-means clustering method allows one piece of data to belong to two or more clusters. This algorithm was developed by Dunn and improved by Bezdek [ 17, 18], and it aims to find the optimal number of clusters for a clustering data.
Algorithm 2
Computation of the MEB of S̃=φ(S)
|
Require: |
A partition of the set S based fuzzy C-mean clustering [17,18] in a collection of subsets Sp
|
|
1: |
for Each subset Sp, p=1,…,P do
|
|
2: |
Compute a ε-core-set Cp for one of the two instantiation |
|
3: |
end for
|
|
4: |
Join the core-sets C=C1∪...∪Cp
|
|
5: |
Compute the minimal enclosing ball of C. This is the Minimal Enclosing Ball of S̃ that define the reduced datasets. |
As shown in the previous sections, the kernel
k˜(xt,xt′)=ytyt′k(xt,xt′)+ytyt′+δtt′C for the binary case (OVO approach) and the kernel
k˜(xt,xt′)=yt′yt′k(xt,xt′)+yt′yt′+δtt′C in the multi-category case (OVA approach).
So, for both the binary (OVO) and multi-category (OVA) multi-class cases, an instantiation of the Algorithm 2 would consist of computing Core-Sets for the subset of examples belonging to each pair of classes, joining them, and finally recovering Algorithm 3 and Algorithm 4, respectively.
Algorithm 3
Computation of the MEB using OVO approach
|
1: |
for Each subset Sp, p=1,…,P do
|
|
2: |
for Each Class l=1,…,L–1 do
|
|
3
|
for Each Class l′=l+1,…,L do
|
|
4: |
Let
Spll′ the subset of Sp corresponding to class l and l′. |
|
5: |
Label
Spll′ using the standard binary codes +1 and −1 for class l and l′ respectively |
|
6: |
Compute a core-set
Cpll′ of
Spll′ Using the kernel
|
|
7: |
end for
|
|
8: |
end for
|
|
9: |
Take the union of the core-set inferred for each pair of classes
|
|
10: |
end for
|
|
11: |
Join core-set CS =C1∪…∪ CP. |
|
12: |
Compute the minimal enclosing ball of CS using the same kernel k̃
|
Algorithm 4
Computation of the MEB using OVA approach
|
1: |
for Each subset Sp, p=1,…,P do
|
|
2: |
Label each example xt ∈ Sp with the code ytp assigned to the class of xt and let yt such label |
|
3
|
Compute a core-set Cp of Sp using the kernel
|
|
4: |
end for
|
|
5: |
Join the core-sets CS =C1∪…∪ CP. |
|
6: |
Compute the minimal enclosing ball of CS using the same kernel k̃
|
6. An UBM-GMM Based Dialect Identification System
A UBM is a GMM representing the characteristics of all the different dialects processed by the dialect identification system. Instead of training dialect dependent models separately, these models are created later by employing Bayesian adaptation from the UBM using the dialect-specific training speech. Any test observations not covered by the models would typically not discriminate up on of any particular dialect identification models.
The UBM technique significantly increases the number of mixtures of the GMM, as well as the dimension of the feature vector; thereby, making it possible to model the characteristics of each dialect more accurately.
For our experiments, we introduced two systems. The first one was used as a baseline, as illustrated in Fig. 4. The second one was an improved system of the first one and was augmented by the reduced data following both the Algorithm 3 and Algorithm 4 applied to the UBM, as illustrated in Fig. 5. For both of the systems, the mixture components of an adapted model of each dialect shared a certain correspondence with the UBM (System 1) or Reduced UBM (System 2), as each model was adapted from the same information. Therefore, the average log-likelihood score for the dialect-adapted models was computed by only scoring the top 10 significant mixtures. According to the correspondence of mixtures between the UBM or Reduced UBM and the model of the dialects, these significant mixtures can be obtained by selecting models mixtures from the UBM or Reduced UBM that have the highest score. By employing this mixture testing strategy, we obtained a significantly reduced computation of scores.
A universal dialect independent background model is created to use a portion of the training data from all dialects. Then, by using MAP adaptation, all of the dialect models were trained by adapting models obtained from the UBM or Reduced UBM and the identification was performed in the same manner as defined above in the previous section. An advantage of employing UBMs in dialect identification systems is the significant reduction of the quantity of training data.
The implementation issue is simple. For each test feature vector and from all UBM mixtures, we determine the top 10 highest scoring mixtures. Using the fact that each dialect model was adapted from the UBM or from the Reduced UBM, the calculation of the dialect model likelihood only required the testing of the 10 mixtures that correspond to the top 10 mixtures from the UBM [ 19]. By employing this approach to the dialect identification system, the score computation complexity was improved, as shown below: Given that both the GMM and UBM have M mixtures, we chose to test the top N mixtures for D dialects. The number of mixture tests (Nbmixture) was:
Alternatively, for the standard GMM system with all mixture tests, the number of mixture tests was:
In our case, we tested five dialects using a 512 GMM mixture and determined the top 10 mixtures from the adapted models. Only the Nbmixture =512+(10×5)=562 mixture tests compared to Nbmixture =512×5=2560 mixture tests for the standard GMM system showed an improvement computation of up to 500%. One of the pitfalls of this method is the possible degradation of accuracy.
7. Experiments
We used our own database for all of the experiments described in this paper, as described in Section 2. Prior to automatic dialect identification, the speech signals are first pre-processed by the zero frequency filtering (ZFF) method [ 20]. The ZFF method is robust against various degradations since most of the frequency components have been attenuated and computed from the speech signal s( n), as: The ZFF is based on difference the speech signal to remove any time-varying low frequency noise of speech signals.
7.1 Parameterization
From the 10 seconds of training and test utterance sets, we extracted vectors composed of 39 dimensional features, which consisted of 12 MFCCs derived from 20 filter banks. Each feature vector was extracted at 10 millisecond intervals using a 30 millisecond Hamming window limited band (300–3,400 Hz) speech. In the first stage, an utterance based on cepstral mean subtraction was applied to the features to remove channel distortion. Then, based on the cepstral feature, we computed 12 SDC coefficients. SDC computations are controlled by four parameters ( N, d, P, k), as discussed in [ 6, 7]. For our study, we used the (10,1,3,3) SDC parameter configuration. The SDC parameterization has been chosen for usage by many researchers on a series of development tests.
7.2 Reducing Data
There are two key topics for conducting a reducing data from a systematic series of experiments. For the first topic, we used the system that was based on reduced data that was taken from Algorithm 3 (multi-class OVO approach). For the second topic, we used the system that was based on reduced data that was taken from Algorithm 4 (multi-class OVA approach). We used the fuzzy C-mean clustering algorithm for both approaches.
7.3 Training
In order to train the UBM, the training data from all of the dialects was pooled together. Since this increases the training set size, the trained UBM will have a higher number of Gaussian Mixtures than GMMs trained on individual dialects.
We trained 512 gender-independent mixtures from each UBM with diagonal covariance matrices. The kernel that we used for the two algorithms (OVO and OVA approaches) was the Gaussian Radial Basis Function with 0.50, a fixed value of σ. The MAP adaptation in training was only done on the mean vectors from the UBM with a relevance factor r of 16.
7.4 Testing
The purpose of the test was to find the maximum score for dialect identification. In this process, five clusters with the mixture order from 2 to 512 were created for each Maghrebian dialect. For each test sample, the SDC coefficients were calculated and compared with each of the five clusters for a mixture order from 2, 4, 8, and 16 to 512. The test sample belonged to the cluster having the higher score. A precision was calculated for each dialect using the formula Precision=(Corect/Total)×100, where Corect defined the number of samples that were correctly classified and Total was the total number of samples given for testing.
Three key topics conduct a systematic series of experiments. For the first topic, we used the first system baseline. For the second and the third topics, we used the second system with Reduced UBM that was taken Algorithm 3 (multi-class OVO approach) or Algorithm 4 (the multi-class OVA approach), respectively. Then, the dialect identification performance was used as a function of the different training and testing sets. Finally, we compared the accuracy of dialect identification for both of the systems. As shown in Tables 1– 3, we show the percentage precision for the five dialects for different mixtures. Our results showed that the system based on reduced GMM-UBM from the OVA multi-class L2-SVM outperformed the GMM-UBM baseline with a precision rate of 74.99%, as compared to 72.84%. The system based on reduced GMM-UBM from the OVO multi-class L2-SVMs exhibited the best performance with a precision rate of 80.49%.
8. Conclusion
Our study was on the Arabic Maghrebian dialect for the purpose of automatic identification. No other studies have been carried out on this before. In this paper, we have introduced two multi-class SVMs approaches reduced to MEB algorithms for improving a baseline GMM-UBM dialect identification system that automatically identifies acoustic differences between dialects by reducing the data in UBM and eliminating the data that is outside the ball defined by the MEB.
We have proposed two algorithms to compute an approximation formulation to the MEB for a given finite set of vectors. Both algorithms are especially well suited for large-scale instances of the MEB problem and can compute a small Core-Set whose size only depends on the approximation parameter.
In addition, it is important to note that Gaussians affected by the MAP adaptation conduct to high performance of the system, as shown in our experiments.
We conducted a series of experiments to test our approach on five Arabic Maghrebian dialects of spontaneous conversations and to compare our results to those of the baseline system. The system based on the multi-class SVM OVO approach outperformed the other approaches.
By comparing our OVO and OVA approaches applied to the dialect identification system to corresponding baseline system, we obtained an improvement of dialect identification, in absolute precision, of 80.49% for the first and 74.99% for the second.
Biography
Nour-Eddine Lachachi
He is an Assistant Master in Computer Science at Oran University, Algeria. He received his State Engineering in 1988 from Study and Research Center on Computer Science, Algiers, and his Magister in Computer Science from Oran University. Currently, he is a doctor student. His research has focused on automatic spoken dialect identification and recognition.
Biography
Abdelkader Adla
He is a Full Professor in Computer Science at University of Oran, Algeria. He received his Ph.D. in Computer Science, Artificial Intelligence from Paul Sabatier University Toulouse III, France. He received also a State Doctorate in Computer-Aided Design and Simulation from University of Oran in 2007. He has published papers on collaborative decision making, decision support systems (DSS), distributed group DSS and multi-agents DSS. His research interests focus on group DSS, facilitation, cooperative and collaborative systems, organizational memory and multiagent decision support systems.
References
1. K. Kirchhoff, and D. Vergyri, "Cross-dialectal acoustic data sharing for Arabic speech recognition," in Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP'04), Montreal, 2004, pp. 765-768.  2. D. Vergyri, K. Kirchhoff, VRR. Gadde, A. Stolcke, and J. Zheng, "Development of a conversational telephone speech recognizer for Levantine Arabic," in Proceedings of Interspeech, Lisbon, Portugal, 2005, pp. 1613-1616.
3. L. Nour-Eddine, and A. Abdelkader, "Reduced universal background model for speech recognition and identification system," in Pattern Recognition, Heidelberg: Springer, 2012, pp. 303-312.  4. JA. Bilmes, in A gentle tutorial of the EM algorithm and its application to parameter estimation for Gaussian mixture and hidden Markov models, International Computer Science Institute, Berkeley, CA, TR-97-021: 1998.
5. PA. Torres-Carrasquillo, E. Singer, MA. Kohler, RJ. Greene, DA. Reynolds, and JR. Deller Jr, "Approaches to language identification using Gaussian mixture models and shifted delta cepstral features," in Proceedings of the 7th International Conference on Spoken Language Processing (ICSLP), Denver, CO, 2002.
6. PA. Torres-Carrasquillo, TP. Gleason, and DA. Reynolds, "Dialect identification using Gaussian mixture models," in Proceedings of the Speaker and Language Recognition Workshop (ODYSSEY), Toledo, Spain, 2004.
7. E. Wong, and S. Sridharan, "Methods to improve Gaussian mixture model based language identification system," in Proceedings of the 7th International Conference on Spoken Language Processing (ICSLP), Denver, CO, 2002.
8. JL. Gauvain, and CH. Lee, "Maximum a posteriori estimation for multivariate Gaussian mixture observations of Markov chains," IEEE Transactions on Speech and Audio Processing, vol. 2, no. 2, pp. 291-298, 1994.  9. DA. Reynolds, TF. Quatieri, and RB. Dunn, "Speaker verification using adapted Gaussian mixture models," Digital Signal Processing, vol. 10, no. 1, pp. 19-41, 2000.  10. VN. Vapnik, in The Nature of Statistical Learning Theory, New York: Springer, 1995.
11. IW. Tsang, JT. Kwok, and PM. Cheung, "Core vector machines: fast SVM training on very large data sets," Journal of Machine Learning Research, vol. 6, pp. 363-392, 2005.
12. M. Badoiu, and KL. Clarkson, "Optimal core-sets for balls," Computational Geometry, vol. 40, no. 1, pp. 14-22, 2008.  13. L. Nour-Eddine, and A. Abdelkader, "Multi-class support vector machines methodology," in Proceedings of the 1st International Congress on Models, Optimization, and Security of Systems (ICMOSS), Algeria, 2010.
14. CW. Hsu, and CJ. Lin, "A comparison of methods for multiclass support vector machines," IEEE Transactions on Neural Networks, vol. 13, no. 2, pp. 415-425, 2002.  15. S. Asharaf, MN. Murty, and SK. Shevade, "Multiclass core vector machine," in Proceedings of the 24th International Conference on Machine Learning (ICML), Corvallis, OR, 2007, pp. 41-48.  16. S. Szedmak, and J. Shawe-Taylor, "Multiclass learning at one-class complexity," in School of Electronics and Computer Science, University of Southampton, UK: 2005.
17. JC. Dunn, "A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters," Journal of Cybernetics, vol. 3, no. 3, pp. 32-57, 1973.  18. JC. Bezdek, in Pattern Recognition with Fuzzy Objective Function Algorithms, New York: Plenum Press, 1981.
19. J. McLaughlin, DA. Reynolds, and TP. Gleason, "A study of computation speed-UPS of the GMM-UBM speaker recognition system," in Proceedings of the 6th European Conference on Speech Communication and Technology (EUROSPEECH), Budapest, Hungary, 1999, pp. 1215-1218.
20. KSR. Murty, and B. Yegnanarayana, "Epoch extraction from speech signals," IEEE Transactions on Audio, Speech, and Language Processing, vol. 16, no. 8, pp. 1602-1613, 2008. 
Fig. 1
(a) Minimal Enclosing Ball. (b) L2-Support Vector Machine. 
Fig. 2
The inner circle is the MEB of the set of squares and its (1+ε) expansion (the outer circle) covers all the points. The set of squares is thus a Core-Set. 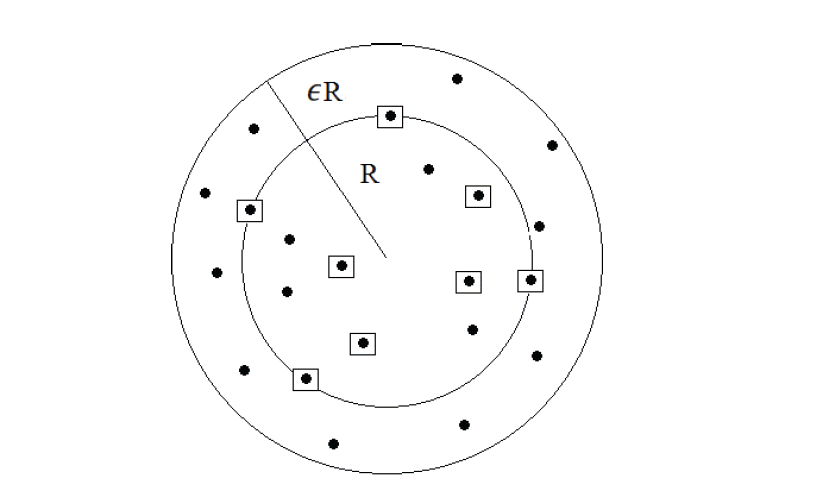
Fig. 3
Visualization of learning process. Getting global MEB through three steps. 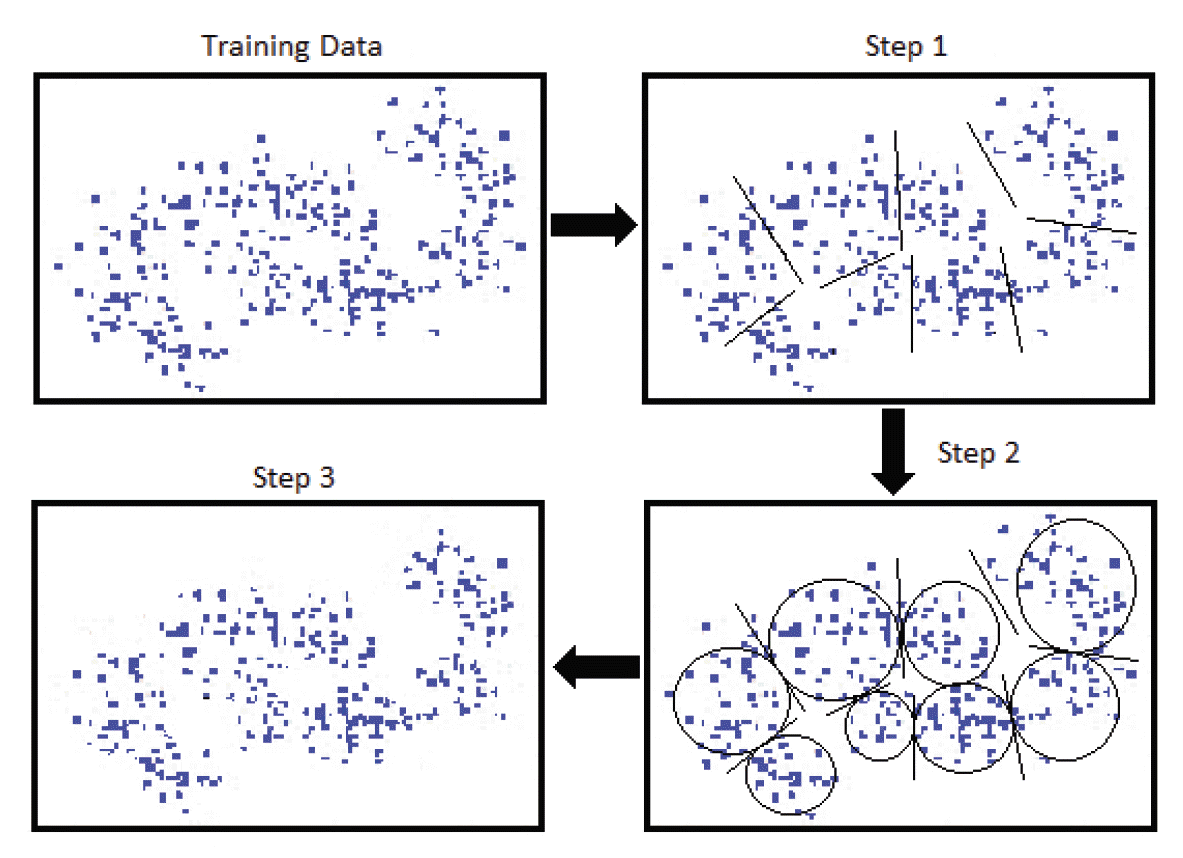
Fig. 4
GMM-UBM dialect identification system (baseline). 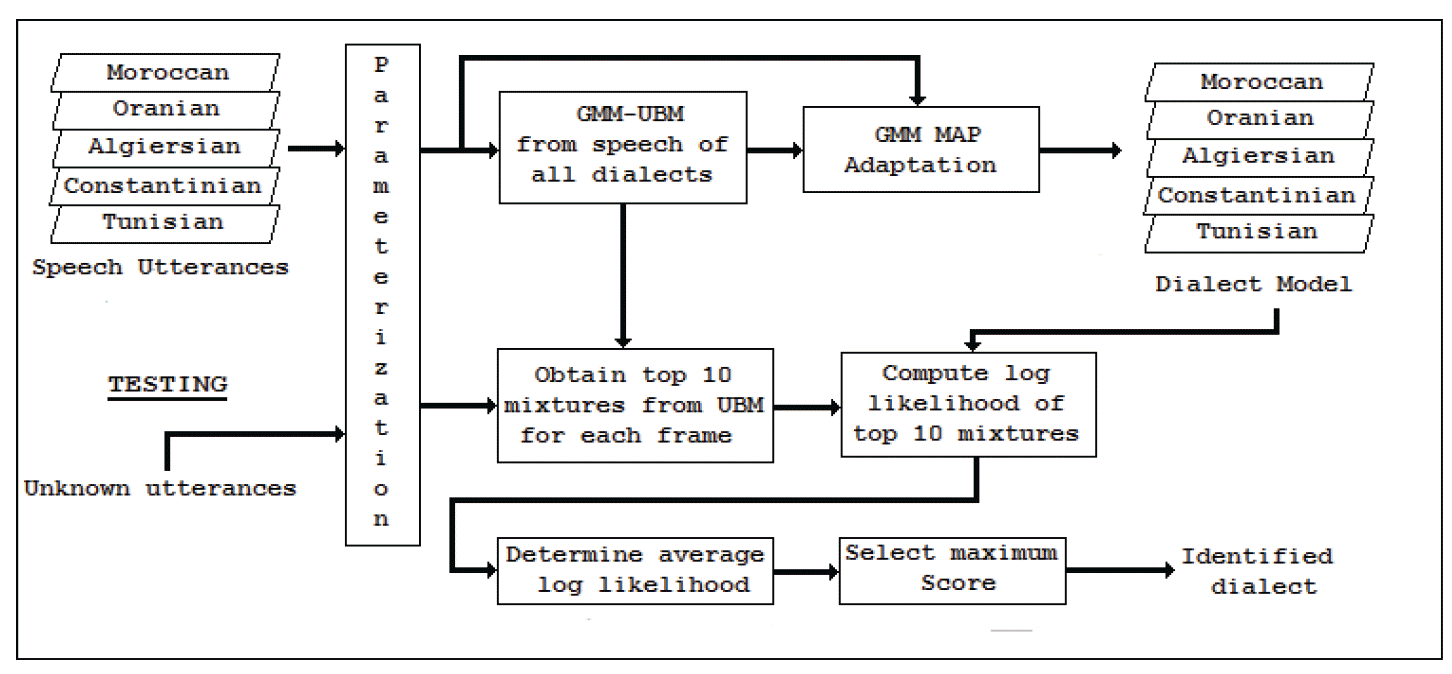
Fig. 5
Improved GMM-UBM dialect identification system. 
Table 1
Accuracy percentage for five dialects for baseline UBM-GMM system
|
Mixture model |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
|
Moroccan |
54.28 |
63.11 |
65.88 |
70.08 |
68.87 |
70.21 |
70.33 |
71.43 |
71.67 |
|
Oranian |
62.77 |
55.23 |
54.93 |
63.17 |
65.33 |
65.15 |
69.53 |
69.93 |
70.54 |
|
Algiersian |
45.67 |
59.13 |
62.73 |
64.83 |
64.98 |
66.94 |
67.12 |
67.78 |
67.85 |
|
Constantinian |
48.03 |
60.34 |
67.27 |
67.93 |
69.01 |
69.41 |
71.83 |
72.16 |
72.18 |
|
Tunisian |
62.57 |
68.25 |
72.33 |
72.91 |
76.16 |
76.22 |
80.91 |
81.39 |
81.95 |
Table 2
Accuracy percentage for five dialects for reduced UBM-GMM system (OVA approach)
|
Mixture model |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
|
Moroccan |
56.08 |
67.33 |
68.93 |
73.93 |
74.06 |
74.89 |
75.14 |
75.55 |
75.78 |
|
Oranian |
63.23 |
58.67 |
59.43 |
64.37 |
65.19 |
70.88 |
71.33 |
71.93 |
72.13 |
|
Algiersian |
49.11 |
61.17 |
64.58 |
65.43 |
65.79 |
68.16 |
68.83 |
69.87 |
70.18 |
|
Constantinian |
51.07 |
60.28 |
68.57 |
69.23 |
71.88 |
72.09 |
72.97 |
73.19 |
73.83 |
|
Tunisian |
65.19 |
69.35 |
74.53 |
74.72 |
76.46 |
77.03 |
81.86 |
82.19 |
83.02 |
Table 3
Accuracy percentage for five dialects for reduced UBM-GMM system (OVO approach)
|
Mixture model |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
|
Moroccan |
63.83 |
68.32 |
71.54 |
76.19 |
78.03 |
78.93 |
82.32 |
82.55 |
83.92 |
|
Oranian |
64.56 |
65.27 |
67.94 |
68.15 |
72.73 |
73.26 |
75.13 |
75.19 |
76.22 |
|
Algiersian |
53.34 |
62.41 |
66.17 |
68.73 |
69.37 |
72.11 |
72.19 |
74.27 |
77.67 |
|
Constantinian |
55.07 |
63.28 |
70.39 |
72.57 |
73.13 |
74.61 |
76.55 |
77.38 |
78.58 |
|
Tunisian |
68.14 |
71.73 |
76.23 |
79.19 |
81.66 |
82.95 |
83.65 |
85.85 |
86.07 |
|
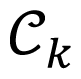 for each set S̃p =φ(Sp) and taking union of all the Core-Sets
for each set S̃p =φ(Sp) and taking union of all the Core-Sets
 = ∪p
= ∪p
 as an approximation to a Core-Set for S̃ = ∪p Sp. Algorithm 2 depicts the generic procedure. In the first step, the algorithm extracts a Core-Set for each subset Sp. In the second step, the MEB of the union of the Core-Sets is computed.
as an approximation to a Core-Set for S̃ = ∪p Sp. Algorithm 2 depicts the generic procedure. In the first step, the algorithm extracts a Core-Set for each subset Sp. In the second step, the MEB of the union of the Core-Sets is computed.





