Selection of the Best Two-Hop AF Wireless Link under Multiple Antenna Schemes over a Fading Channel

doi:2015.11.1.57

Abstract

In evaluating the performance of a dual-hop wireless link, the effects of large and small scale fading has to be considered. To overcome this fading effect, several schemes, such as multiple-input multiple-output (MIMO) with orthogonal space time block codes (OSTBC), different combining schemes at the relay and receiving end, and orthogonal frequency division multiplexing (OFDM) are used in both the transmitting and the relay links. In this paper, we first make compare the performance of a two-hop wireless link under a different combination of space diversity in the first and second hop of the amplify-and-forward (AF) case. Our second task in this paper is to incorporate the weak signal of a direct link and then by applying the channel model of two random variables (one for a direct link and another for a relayed link) we get very impressive result at a low signal-to-noise ratio (SNR) that is comparable with other models at a higher SNR. Our third task is to bring other three schemes under a two-hop wireless link: use of transmit antenna selection (TAS) on both link with weak direct link, distributed Alamouti scheme in two-hop link and single relay antenna with OFDM sub-carrier. Finally, all of the schemes mentioned above are compared to select the best possible model. The main finding of the paper is as follows: the use of MIMO on both hops but application TAS on both links with weak direct link and the full rate OFDM with the sub-carrier for an individual link provide a better result as compared to other models.

Key words: Ergodic Capacity, OFDM, OSTBC, Space Diversity, TAS, Wideband Slope

1. Introduction

Recently, researchers have paid significant attention in the field of two-hop wireless links in both the cases of with and without channel state information. To enhance the reliability of a wireless network, relaying techniques are specially used when the link between the sender and receiver are far away or when the direct link is heavily contaminated with noise and fading. Two of the most widely used techniques are amplify-and-forward (AF) relaying and decode-and-forward (DF) relaying. Sometimes, the gain of a relay is kept constant, irrespective of the condition of the wireless channel (fixed gain AF relay). However, sometimes a relay station taking feedback/acknowledgement from the receiver to adjust the gain is called the variable gain AF relay. The concepts of an AF relay are summarized in [1–3]. For the case of partial channel state information (PCSI) authors in [3] use the AF technique to estimate the outage probability for a cognitive relay network. In [4], the average fading power of a ‘source-to-relay’ and relay-to-destination (R-D) link are derived in a Rayleigh fading environment. The performance of a multi-hop cooperative relay network where the destination receives a signal from both the relay and sender is derived in [5,6] considering two random variables for signal-to-noise ratio (SNR) where one is from the relay and the other from the sender for k-fading. In [7], the AF model is used under the line of sight interference environment. We derived the gain of a relay station in terms of transmitted signal power, the power of interferences, the source-to-relay path gain and noise variance. In [8], the idea of a two-hop wireless link is applied in a multi-way relay channel where multiple users exchange information through a relay terminal. The relaying concept is applied in a cognitive radio network using different cooperative protocols like selection amplify-and-forward (SAF), selection decode-and-forward (SDF) in [9,10] and DF in [11]. Sometimes, among several antennas the best antenna at the transmitting end is selected based on the concept of the water-filling model (to maximize the instantaneous SNR), which is known as transmit antenna selection (TAS). The combination of TAS and MRC under multiple-input multiple-output (MIMO) is analyzed in [12] where the outage probability and bit error rate (BER) of different schemes are compared with the TAS/MRC schemes. The combination of TAS at the transmitter side and SC/MRC at the receiver side is analyzed in [13] with a closed form of solution of the outage probability.

A multiple-antenna system is used in two-hop link to improve the reliability of the link (i.e., reducing the ergodic error probability or the outage probability and to enhance the data rate by transmitting a parallel data stream over the antennas. To reduce the ergodic error probability, the SNR needs to be enhanced. The SNR needs narrow beamforming, an increase in the variation of SNRs, and path diversity. The degree of diversity can be improved in a two-hop wireless link by the applying multiple antennas at the transmitter/receiver/relay stations.

Several approaches can be imposed in context of MIMO in a two-hop wireless link. For example, one approach is to place multiple antennas at the receiver side by making an appropriate separation between the adjacent antennas depending on the channel state characteristics to get an uncorrelated channel response, which is called, receive diversity. In accordance with the multiple receivers, there are different combining schemes, such as selection combining, equal gain combining, maximum ratio combining (MRC), etc. All of which are used to represent the optimum receiver. The second approach is to place multiple antennas at the transmitter side but a signal that is transmitted simultaneously over several antennas will not get the desired diversity gain. In this case, special coding is required at the transmitter. These special codes are called space-time codes. There are widely used codes like Alamuiti, space-time block codes (OSTBCs) and space-time trellis codes (STTCs) are used to get uncorrelated symbols [14]. The STBC of [15] is also applicable in a single hop wireless link to reduce the BER and to increase the throughput.

Sometimes, the best transmitting antenna (TAS) is selected in consideration of the water-filling model. TAS is also used in this paper. Another approach is to use multiple antennas only on the relay station and single antenna on both ends. The reverse model (i.e., multiple antennas) on both ends and a single antenna on the relay are also possible.

In this paper, we investigate several models to observe the relative performance of the two-hop wireless link in a Rayleigh and Nakagami-m fading environment. We used the 8-PSK modulation techniques at the transmitter. The paper is organized as follows: Section 2 presents the detailed mathematical analysis of a two-hop wireless link. Section 3 focuses on the results obtained from the analysis of the previous sections, while Section 4 concludes the findings of the paper.

2. System Model

2.1 Generalized Two-Hop Links

In a two-hop wireless link the received signal vector at the relay can be written as:

(1)

yR=EHSRx+nSR,

where E is the transmitted power, H_SR is the channel matrix from the source to relay, x is the source signal, and n_SR is the noise vector of source to relay link. Similarly, the received signal vector at the destination is:

(2)

yD=EHRDyRD/+nRD

where, yRD/ is the delayed version of the received signal at the relay after some processing. The noise vector on both the links has the properties: E(nSRnSR†)=INR N0 and E(nRDnRD†)=IND N0, where, N₀ is the variance of the additive white Gaussian noise (AWGN), I_N_{_R} is the identity matrix with N_R antennas at the relay station, and N_D is the number of antennas at the destination.

If the SNR of the links are: Γ_SR = E_S||H_SR||² / N₀ and Γ_RD = Ē_R ||H_RD||² / N₀, then the overall SNR will be [16,17]:

(3)

ΓSD=ΓSRΓRDΓSR+ΓRD+1.

Let the probability density function (pdf) and cumulative probability density function (cdf) of Γ_i (i=SR and RD) be f_{Γ_i}(γ) and (γ)F_{Γ_i}, respectively. Then, the cdf of the combined link is [18]:

(4)

FSD(γ)=1-∫0∞{1-FΓSR(γ+γ2ω)}fΓRD (ω+γ)dω,

where, ω = Γ_RD −γ. In case there is a transmit antenna selection among N_s antennas, the cdf will be: F_{Γ_SR}(γ) = {F_Γ₁ (γ)}^N_S.

A similar analysis is also done in [19]. Thus,

(5)

FSD(γ)=∫pr{γSRγRDγSR+γRD+1≤γ∣γRD}fΓRD(γRD)dγRD=∫0∞pr{γSR≥γ(γRD+1)γRD-γ∣γRD}fΓRD(γRD)dγRD+∫pr{γSR≥γ(γRD+1)γRD-γ∣γRD}fΓRD(γRD)dγRD=∫0∞fΓRD(γRD)dγRD+∫γ∞{FΓRDγ(γRD+1)γRD-γ}fγRD(γRD)dγRD.

The ergodic capacity of the link is [5]:

(6)

C=maxλD∫λDln(1+y)fΓRD(y)dy=∫0∞1-FγD(y)1+ydy,

where λ_RD is the output SNR of the destination device. For example: γ_D = γ_MRC if an MRC scheme is being used. The symbol error rate (SER) of the destination [16,18] is given by:

(7)

PS=E(aQ(2bγD)).

The average error probability can be written in terms of the cdf of γ_D as [16]:

(8)

Ps=a2bπ∫0∞e-bxxFγD(x)dx,

where, a and b depend on the specific modulation scheme.

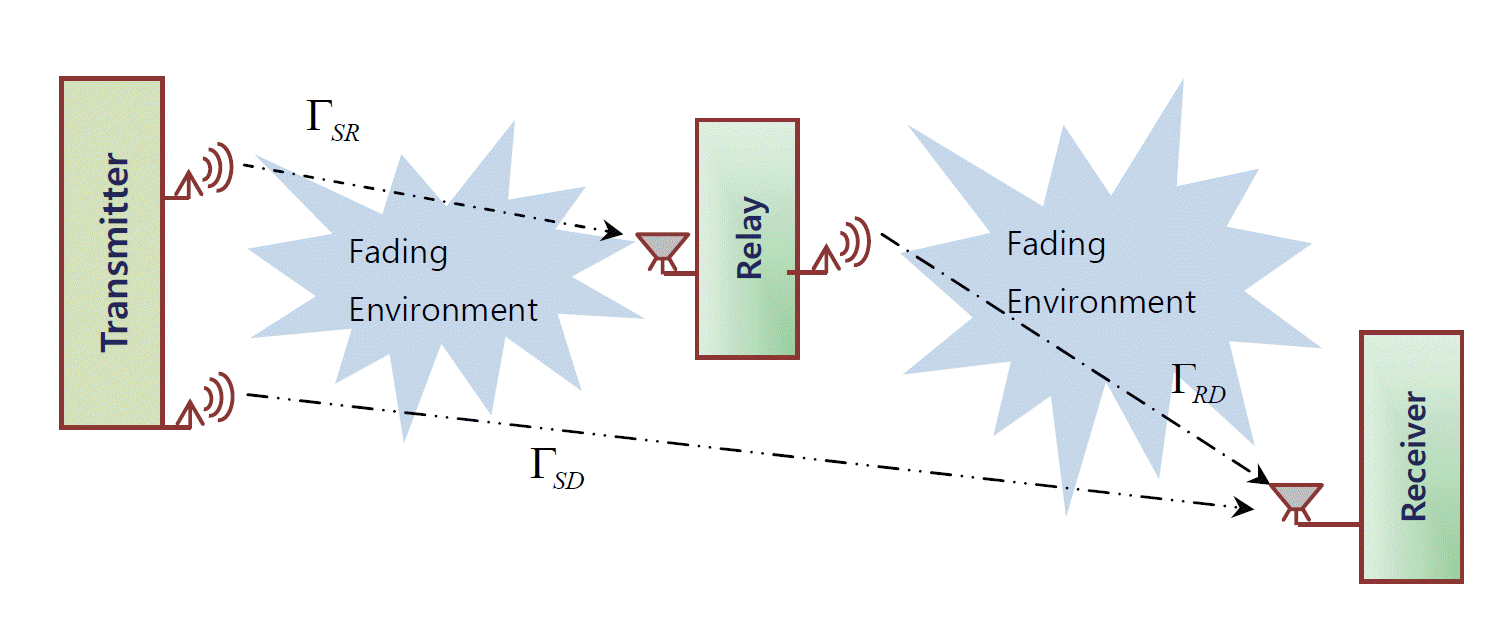
To enhance the reliability of the system, we can use the model in Fig. 1, where the signal is received from both the direct and relayed links.

Let us define two different random variables (RVs) where the one for the relayed link is Δ = Γ_SRΓ_RD/(Γ_SR + Γ_RD +1), and the other for the direct link is R. The combined cdf is [6]:

(9)

FG(ξ,γD,γm)=∫s=0ξ∫ρ=0ξ-sfΔ(s)fR(ρ)dρds,

where, γ_D and γ_m are the average SNR of the direct link and the multi-hop link, respectively. The combined pdf is:

(10)

fG(ξ,γD,γm)=ddξ{∫s=0ξ∫ρ=0ξ-sfΔ(s)fR(ρ)dρds}.

The SER, from Eq. (8), becomes:

(11)

Ps(γD,γm)=12∫0∞erfc(cξ2)fG(ξ,γD,γm)dξ.

The ergodic capacity, from Eq. (6), becomes:

(12)

C(γD,γm)=∫0∞1-FG(ξ,γD,γm)1+ξdξ.

Using the above equations we can determine the capacity and the SER of a two-hop wireless link using a different combination of the number of antennas for a transmitter, receiver, and relay, along with incorporating the weak signal of a direct link.

Another approach in determining the approximate channel capacity of a MIMO link as shown in [20] is,

(13)

C(γ)=S0 log2(γγmin),

where, γ_min is the minimum normalized SNR for being able to reliably convey the message and S₀ is the wideband slope discussed in [20,21]. These parameters can be evaluated as:

(14)

γmin=Nt ln 2E{trace(HH H)},

and:

(15)

S0=2E({trace(HH H)})2E{trace((HH H)2)}.

Again:

(16)

E{trace(HH H)}=NtNrE(x2),

and:

(17)

E{trace((HH H)2)}=NtNr{E(x4)+(Nt+Nr-2)(E(x2))2},

where, x is an RV and indicates the channel gain h_i,j of the MIMO link. N_t and N_r are the number of transmitting and receiving antennas. The n-th moment of the RV, E(xⁿ), depends on the pdf of the fading environments. In this paper, the above concept is applied for a two-hop wireless link.

2.2 A Two-Hop Link Aided by a Weak Direct Link

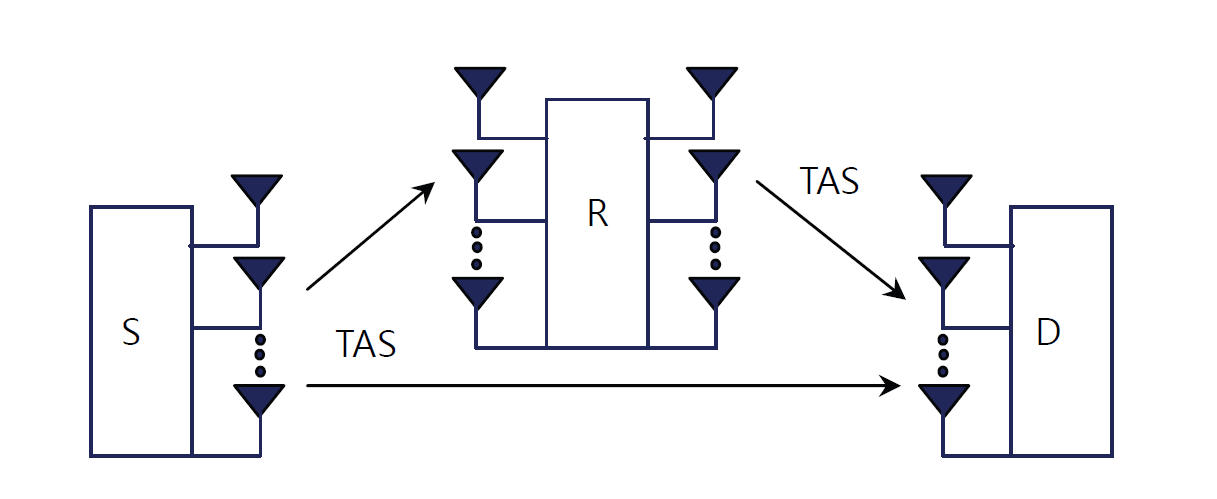
This subsection deals with AF relay using the concept of TAS in [22]. The system model is shown in Fig. 2 where in the first time slot (TS) the sender sends the symbol S_k. Hence, the relay, R, and destination, D, both receive the symbol. In seconds, the TS relay sends the stored symbol, S_k, using TAS. Therefore, the receiver gets the same symbol in the two consecutive TSs.

If the i-th sending antenna and j-th relayed antenna are used, then the equivalent SNR at the receiving end will be:

(18)

γev(i,j)=γSD(i)+γSR(i)γRD(j)γSR(i)+γRD(j),

where, γ_xy(i) = γ̄_xy(i)|h_xy(i)|².

The above approach is applied for a single antenna case in [23] based on OFDM. In the first TS, the received signal at the destination and relay are yS-D=HSD S_k+v_n-SD and y_S-R=H_SR S_k+v_n-SR.

In the second TS, the relayed signal is received at the destination as:

(19)

yR-D=HRDyS-R μ+vn-RD=HSRHRD μSk+vn-SRHRD μ+Vn-RD=μHSRHRD Sk+vn-RD′,

where, H_xy is the transfer function between the nodes x and y, and μ is the amplification factor of the relay. We can express the received signal of two consecutive TSs in vector form as:

(20)

[yS-DyR-D]=[HSDμHSRHRD]Sk+[vn-SDvn-RD′].

The above equation resembles a 1×2 virtual MIMO. Hence, SNR will be the sum of two virtual channels like:

(21)

γev=γ¯D|HSD|2+γ¯R|μ|2|HSR|2|HRD|2,

where:

γ¯D=PSND,γ¯R=PS|μ|2|HRD|2NR+ND.

The quantity N_D is the power spectral density (psd) of the noise of the direct link between the source and the destination, and the quantity N_R is the psd of the noise of the source to the relay link. Both of the models above can be considered as a half rate space-time block code since one symbol is transmitted per every two TSs.

2.3 The Alternate Alamouti Scheme in Relayed Communication

Next we will consider another model [24] where two relays are used for a dual-hop AF communication system, as shown in Fig. 3. The system operates in two phases:

Phase 1: The sender sends two symbols S₁ and S₂, i.e., S = [S₁ S₂] in two consecutive TSs. The relays receive the signal like:

(22)

[Y1Y2]=[y1(1)y1(2)y2(1)y2(2)]2nd_relay_link1st_relay_link,

where:

[y1(1)y1(2)]=[s1s2]h1+n1 and [y2(1)y2(2)]=[s1s2]h2+n1

Phase 2: The relays generate an Alamouti code using [Y1Y2] and forward the signal to the destination. The transmitted signal matrix of relays will be:

(23)

TR=G[y1f1(1)-y2*f2(2)y1*f1(2)y2*f2(1)],

where G is the gain of the relay.

The received signal of destination will be:

r(1)=f1y1(1)+f2{-y2*(2)}+nD(1),r(2)=f2y2*(1)+f1y1(2)+nD(2),

which implies r*(2)=f2* y2(1)+f1* y1(2)+nD*(2). Therefore,

[r1(1)r2*(2)]=G[h1 f1-h2* f2h2 f2*h1* f1*] [s1s2*]+[n1n2*],

which can be written in matrix form as:

(24)

r=Hs+n.

For the channel matrix:

(25)

H+H=G2(|h1|2|f1|2+|h2|2|f2|2)I2.

Similarly, the orthogonal relation can be shown for noise matrix like:

(26)

n+n=N0{G2(|f1|2+|f2|2)+1}I2.

Therefore, the SNR will be:

γ=γevG2|h1|2|f1|2+|h2|2|f2|2G2|f1|2+|f2|2+1.

In the case of a conventional Alamouti scheme:

(27)

γ=γav(|h1|2+|h2|2).

Because of the orthogonality of links only an AWGN model is applicable in both of these cases to determine the symbol error rate.

2.4 Single Relay Full Rate Model

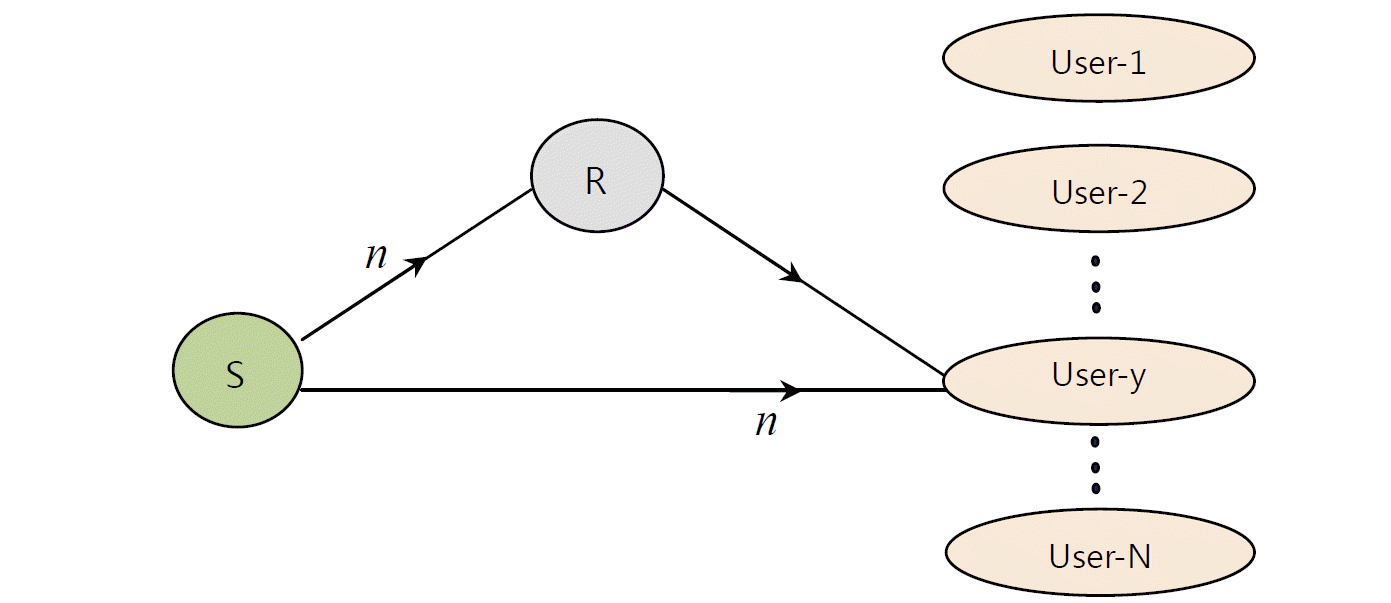
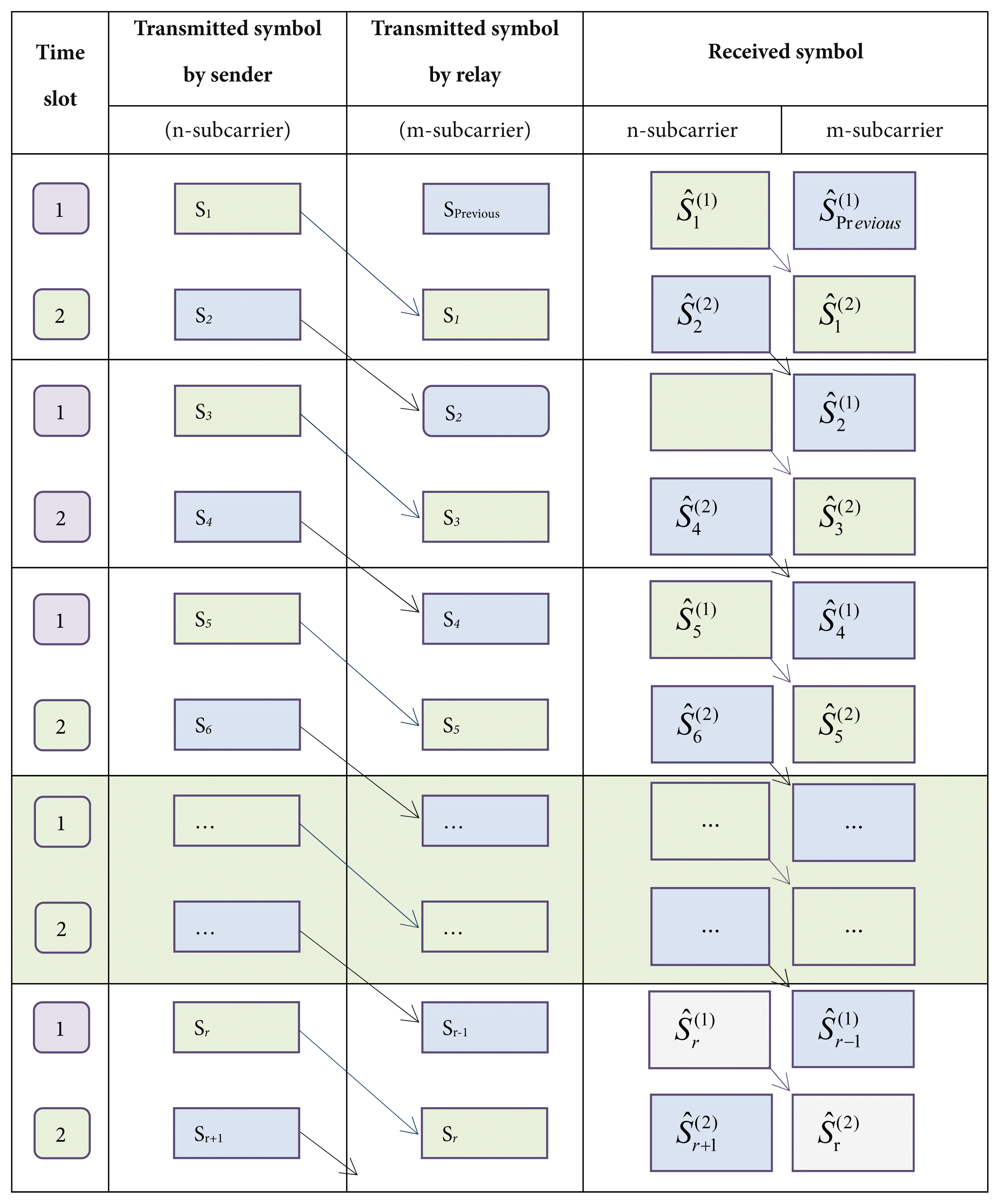
In this paper the two-hop model used in [25] is modified to achieve full-rate space diversity using OFDM. Let the sender send the symbol S_k at the OFDM subcarrier n to user j. Hence, both the relay and user j received the signal in TS-1 like before.

In TS-2 the relay sends the stored symbol, S_k, to user j using another subcarrier, m. Since the user j gets the same symbol S_k in two consecutive TSs it has the option to detect the symbol more precisely. The more complete arrangement of the system is shown in Fig. 4. In the first TS, the received signal applying auto-correlation is:

(28)

〈Re{HSDSkej2πfnt+θn}+n′,OSC(fn)〉=S^k(1).

In the second TS, the received signal will be:

(29)

〈Re{S˜kej2πfnt+θm}+n′,OSC(fm)〉=S^k(2),

where, OSC(f_i) is the i-th orthogonal subcarrier, S^k(i) is the estimated received signal at i-th TS, S̃_k, is the noisy version of symbol S_k, and θ is the phase error.

In the previous half rate model, the sender was silent when the relay was in the transmitting mode. Because of the use of an orthogonal subcarrier of the OFDM the sender can now simultaneously transmit with the relay. The transmitted and received signals of the system are visualized in Table 1. An arrow in Table 1 connects the same symbol between two consecutive TSs. Now the symbol detection can be done using the maximum likelihood as:

(30)

min{arg(S^i(i)-ϕɛψS),arg((S^i(2)-ϕɛψS))}.

The instantaneous received SNR is γ₁ = |h_SR|²|h_RD|²γ_avg and γ₂ = |h_SD|² γ_avg. Since <OSC (f_m) OSC(f_n)> = 0, hence, the AWGN model is applicable to detect the symbol error probability. Now the probability of the symbol error is: P_e = P(γ₁ < ɛ )P(γ₂ < ɛ); where, ɛ is the threshold SNR at the receiving end.

3. Results and Discussions

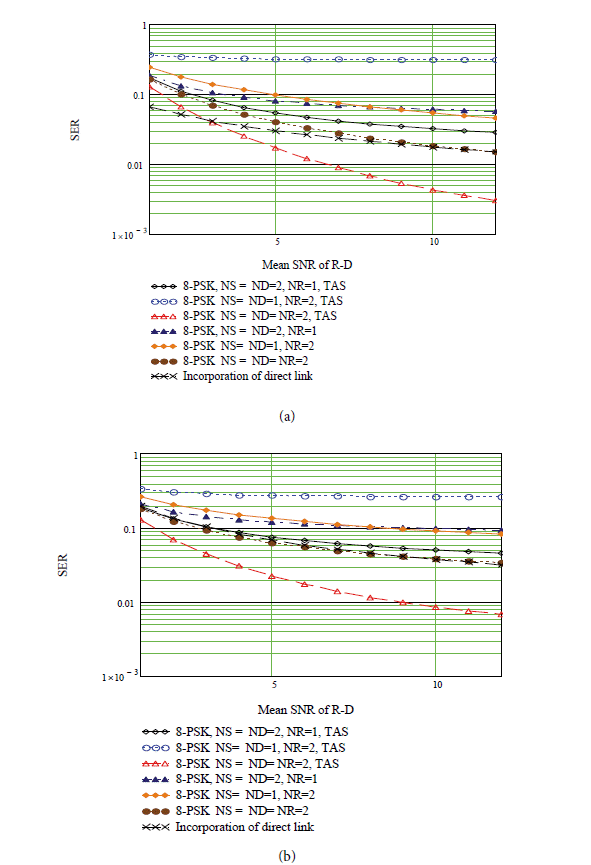
Fig. 5(a) and (b) show the variation of the ergodic channel capacity of the R-D line against the SNR of the corresponding link for Nakagami-m and Rayleigh fading cases, respectively. We used three combinations of antennas when applying the concept of [17,26,27]: N_S = N_D = 1, N_R = 2; N_S = N_D = 2, N_R =1; and N_S = N_D = N_R = 2. The first three cases are drawn for the case of TAS and the next three curves are drawn considering all of the antennas. The performance of the channel is almost fixed in both the Nakagami-m and the Rayleigh fading channels for the case of the TAS because of the use of strongest SNR link. However, in the case of an ordinary MRC scheme, the performance of the link is found to be better in a Nakagami-m fading case. This is because m = 2 with a strong direct link between R and D [28].

It is important to note that the channel capacity was found to be very poor for the case of N_S = N_D = 1, N_R = 2, TAS. Since one link is selected for the case of TAS, the two-hop link resembles the case of a single antenna link and will not get the benefit of the Alamouti or the MRC schemes. The channel capacity was found to be the best for the N_S = N_R = N_D = 2 case. The capacity can be further improved if we combine the Alamouti and MRC schemes, which is not shown in Fig. 5. We were more interested in observing it via simulation, as shown in Fig. 6. Applying the ordinary MIMO formula of a matrix trace under the 2 ×2 MIMO link of both hops resulted in a moderate performance for the Rayleigh fading case, while it yielded very good results for the Nakagami-m fading. Incorporating the weak signal of the direct link (a single antenna case was considered here) enhances the capacity for a Nakagami-m fading case, as compared to that of a Rayleigh fading. This is because there are several strong direct links for the case of the Nakagami-m fading environment. The performance of the single antenna case then becomes comparable to that of the multiple antenna case.

Fig. 7(a) and (b) show the variations of the SER of R-D links against the SNR of the corresponding link for the Nakagami-m and Rayleigh fading cases, using the same combination as shown in Fig. 5. The profile of the SER of TAS case was found to be almost the same for both of the fading cases. However, in the case of all of the antennas being utilized, the SER was found to be better for the Nakagami-m case. A similar explanation is also applicable for the case N_S = N_D = 1, N_R = 2, TAS line as shown in Fig. 5. The SER is found the lowest for the case of N_S = N_R = N_D = 2. It can be further lowered using the Alamouti and MRC schemes, which we verified using a simulation, as shown in Fig. 6. Similarly, incorporating the weak direct signal with the SNR of the 0.2 single antenna link shows that its performance is comparable to the multiple antenna case.

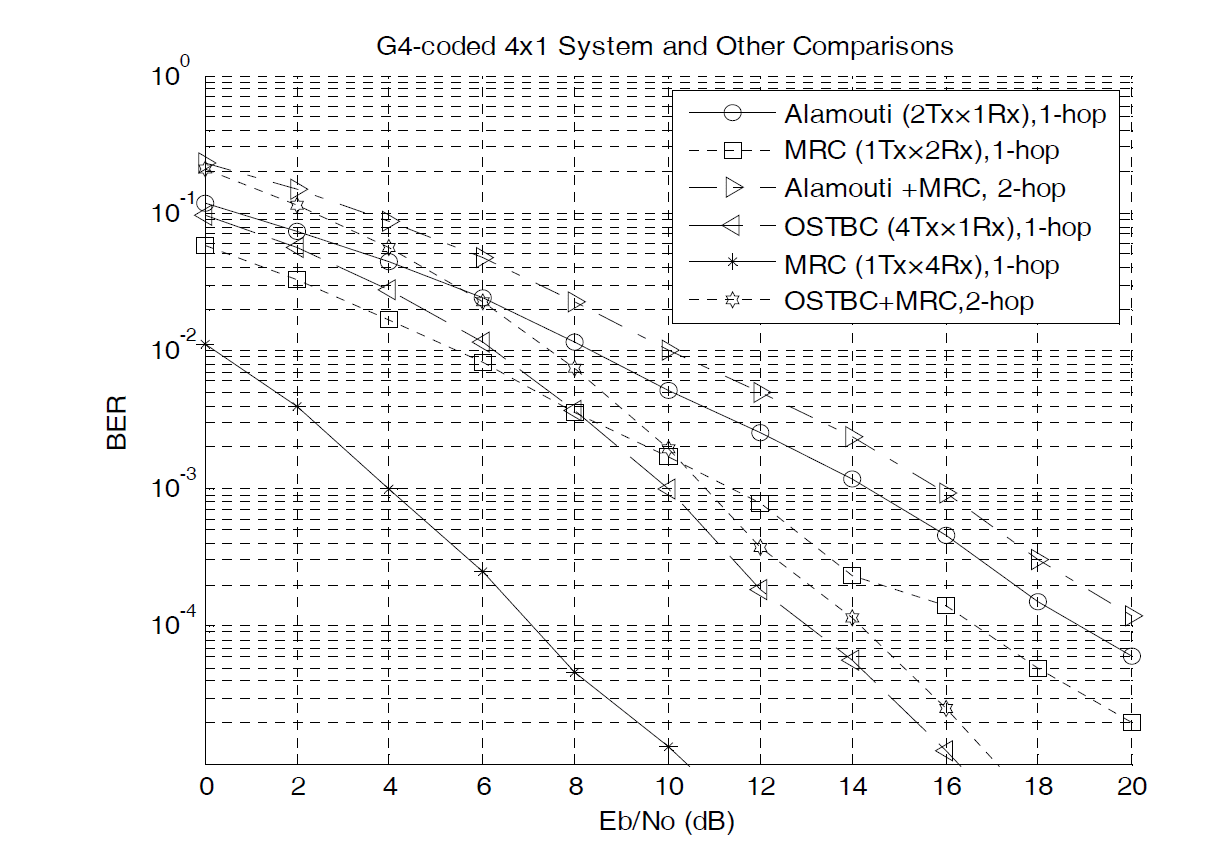
We ran a simulation on MATLAB (using the concept of Monte Carlo) to get the profile of the SER. We used the Alamouti scheme for a single link, the MRC 1Tx×2Rx case, the two-hop link where the first hop is the Alamouti scheme and the second one is MRC, a single hop with OSTBC 4Tx×1Rx, a single hop MRC of 1Tx×4Rx, and a two-hop OSTBC with MRC, as shown in Fig. 6. The curves seem much stepper because of using the BPSK scheme. The combination of the Alamouti and MRC schemes was found to be the best, as shown in Fig. 6. Of course increasing the number of antennas can further enhance the performance, but the cost of the link will be higher.

Simulation work was done separately for determining the normalized channel capacity for four different fading cases. We fully used the MIMO (transmitter, relay and receiver) of four antennas in each stage by using the idea of trace of the channel matrix. Comparisons of our theoretical and simulation results are shown in Fig. 8 for four different fading environments. The statistical parameters of the fading channels are taken as, Gaussian: σ = 0.2, μ = 4; Weibul: λ =1.5, m = 3.75; Nakagami-m: γ_av = 6, m = 4; and Rayleigh: γ_av = 6. The analytical and simulation results of Fig. 8 satisfied the concept of Fig. 5 (i.e., the channel capacity under Nakagami-m fading is better than the case of Rayleigh fading). Both of the fading environments showed moderate results in the sense that they were better than the Weibul fading case, but worse than the Gaussian fading case.

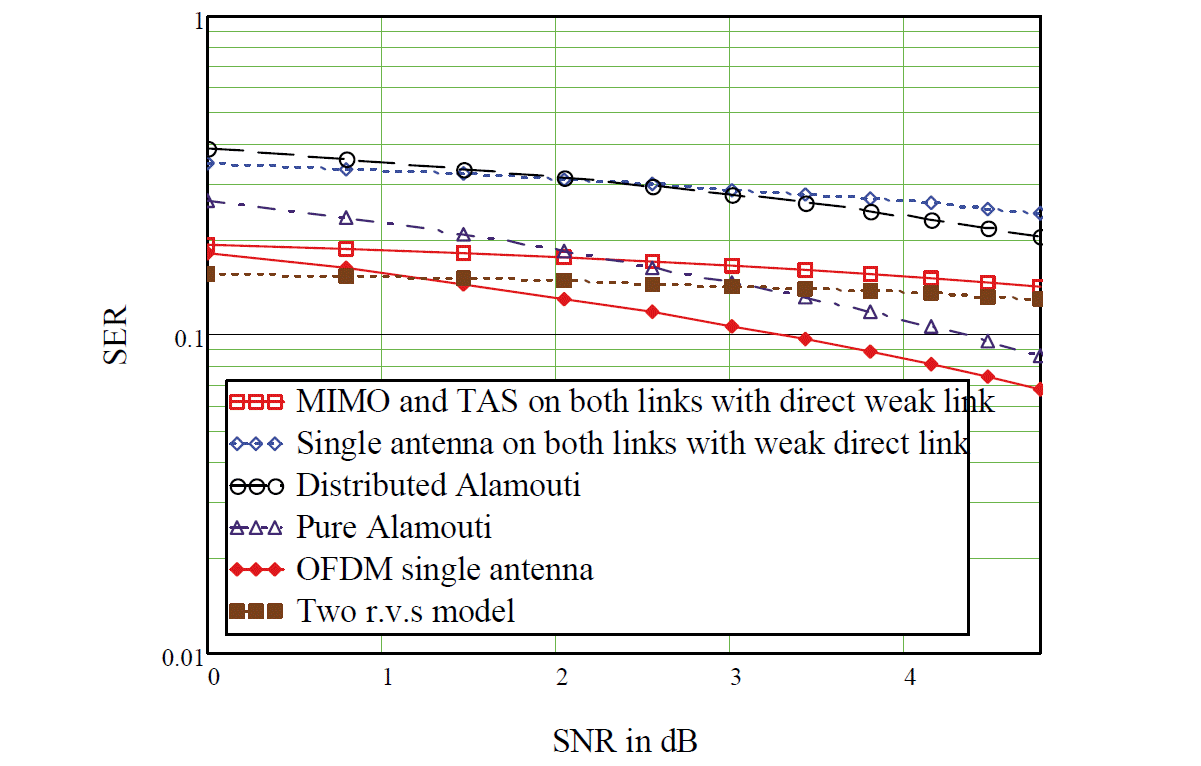
Finally, MIMO and TAS with a weak direct link, a single antenna case with a direct link, the distributed Alamouti scheme, the conventional Alamouti scheme, the full rate OFDMA with two subcarriers scheme, and two r.v.s models were compared in context of SER varying of SNR from 1 to 5 dB (direct link for concerned models). The complete results are shown in Fig. 9. Rayleigh fading was only considered in the case of two r.v.s models and the other modes were almost orthogonal (i.e., immune from severe fading). Among all of the models we used, the OFDM had the best performance. However, this was at the expense of using two sub-carriers for each link.

5. Conclusions

In this paper, we were able to bring most of the recent concepts about two-hop wireless links under small scale fading to find an optimal model. Our findings are as follows: the inclusion of the weak signal of a direct link with the relayed signal resembles a parallel link where SNR becomes an additive like the conductance of a parallel electrical circuit and gives the best performance as compared to any other existing models. Using multiple antennas on both ends and a single antenna on the relay is much better than the case of using a single antenna on both ends and multiple antennas on the relay. Selection of transmit antenna enhances the performance of wireless link compared to the 2×2 MIMO case. This satisfies the concept of the water filling model. The approximate ergodic capacity model, using trace of autocorrelation matrix, gives moderate results, but doing the mathematical modeling for it is much simpler. Finally, the combination of the Alamouti scheme and the MRC scheme gives the best result, but the complexity of practical design is much higher compared to other models. Finally, the concept of MIMO and TAS with a weak direct link case, a single antenna case with a direct link, the distributed Alamouti scheme, the conventional Alamouti scheme, the full rate OFDMA with two subcarriers scheme are included with conventional two-hop wireless communications so that a network planner has a wide range of options to choose the best communication system.

Biography

Abu Sayed Md. Mostafizur Rahaman

He is pursuing Ph.D. in the field of Telecommunication. He has received M.Sc. degree from Stuttgart University at Stuttgart, Germany in Information Technology (INFOTECH) in the branch of Embedded System Engineering in 2009 and B.Sc. degree in Electronics and Computer Science, from Jahangirnagar University, Savar, Dhaka, Bangladesh in 2003. Since 2004, he is a faculty member having current Designation “Associate Professor” in the Department of Computer Science and Engineering of Jahangirnagar University, Savar, Dhaka, Bangladesh. During his graduation, he worked at BOSCH (biggest automobile company in Germany) as Trainee engineer (Industrial internship) as part of his graduate degree in embedded System Engineering. Currently his research focuses on telecommunication, Embedded and Parallel Systems, Reconfigurable Computing, Multicore Architecture and Software Engineering.

Biography

Md. Imdadul Islam

He has completed his B.Sc. and M.Sc. Engineering in Electrical and Electronic Engineering from Bangladesh University of Engineering and Technology, Dhaka, Bangladesh in 1993 and 1998, respectively and has completed his Ph.D. degree from the Department of Computer Science and Engineering, Jahangirnagar University, Dhaka, Bangladesh in the field of network traffic engineering in 2010. He is now working as a Professor at the Department of Computer Science and Engineering, Jahangirnagar University, Savar, Dhaka, Bangladesh. Previously, he worked as an Assistant Engineer in Sheba Telecom (Pvt.) LTD (A joint venture company between Bangladesh and Malaysia, for Mobile cellular and WLL), from Sept.1994 to July 1996. Dr Islam has a very good field experience in installation of Radio Base Stations and Switching Centers for WLL. His research field is network traffic, wireless communications, wavelet transform, OFDMA, WCDMA, adaptive filter theory, ANFIS and array antenna systems. He has more than 150 research papers in national and international journals and conference proceedings.

Biography

M. R. Amin

M. R. Amin received his B.S. and M.S. degrees in Physics from Jahangirnagar University, Dhaka, Bangladesh in 1984 and 1986, respectively and his Ph.D. degree in Plasma Physics from the University of St. Andrews, U. K. in 1990. He is a Professor of Electronics and Communications Engineering at East West University, Dhaka, Bangladesh. He served as a Post-Doctoral Research Associate in Electrical Engineering at the University of Alberta, Canada, during 1991–1993. He was an Alexander von Humboldt Research Fellow at the Max-Planck Institute for Extraterrestrial Physics at Garching/Munich, Germany during 1997–1999. Dr. Amin awarded the Commonwealth Postdoctoral Fellowship in 1997. Besides these, he has also received several awards for his research, including the Bangladesh Academy of Science Young Scientist Award and the University Grants Commission Young Scientist Award for the year 1996. He is a member of the IEEE. His current research includes traffic engineering in wireless communications and nonlinear interactions in plasmas.

References

1. A. Zafar, RM. Radaydeh, Y. Chen, and MS. Alouini, "Energy-efficient power allocation for fixed-gain amplify-and-forward relay networks with partial channel state information," IEEE Wireless Communications Letters, vol. 1, no. 6, pp. 553-556, 2012.

2. S. Huang, H. Chen, and Y. Zhang, "Optimal power allocation for spectrum sensing and data transmission in cognitive relay networks," IEEE Wireless Communications Letters, vol. 1, no. 1, pp. 26-29, 2012.

3. H. Yu, W. Tang, and S. Li, "Outage probability and SER of amplify-and-forward cognitive relay networks," IEEE Wireless Communications Letters, vol. 2, no. 2, pp. 219-222, 2013.

4. N. Cao, F. Wang, Y. Chen, X. Hu, and M. Long, "Estimation of the average fading powers for AF relay system," IEEE Communications Letters, vol. 17, no. 1, pp. 135-138, 2013.

5. HY. Lateef, M. Ghogho, and D. McLernon, "On the performance analysis of multi-hop cooperative relay networks over generalized-K fading channels," IEEE Communications Letters, vol. 15, no. 9, pp. 968-970, 2011.

6. PM. Shankar, "Error rates in generalized shadowed fading channels," Wireless Personal Communications, vol. 28, no. 3, pp. 233-238, 2004.

7. NS. Ferdinand, N. Rajatheva, and M. Latva-aho, "Effects of line-of-sight interference on the performance of amplify-and-forward relay network," IEEE Communications Letters, vol. 17, no. 5, pp. 940-943, 2013.

8. D. Gunduz, A. Yener, A. Goldsmith, and HV. Poor, "The multiway relay channel," IEEE Transactions on Information Theory, vol. 59, no. 1, pp. 51-63, 2013.

9. Z. Yan, X. Zhang, and W. Wang, "Exact outage performance of cognitive relay networks with maximum transmit power limits," IEEE Communications Letters, vol. 15, no. 12, pp. 1317-1319, 2011.

10. Z. Dai, J. Liu, C. Wang, and K. Long, "An adaptive cooperation communication strategy for enhanced opportunistic spectrum access in cognitive radios," IEEE Communications Letters, vol. 16, no. 1, pp. 40-43, 2012.

11. Y. Liu, and W. Chen, "Adaptive resource allocation for improved DF aided downlink multi-user OFDM systems," IEEE Wireless Communications Letters, vol. 1, no. 6, pp. 557-560, 2012.

12. Z. Chen, J. Yuan, and B. Vucetic, "Analysis of transmit antenna selection/maximal-ratio combining in Rayleigh fading channels," IEEE Transactions on Vehicular Technology, vol. 54, no. 4, pp. 1312-1321, 2005.

13. N. Yang, PL. Yeoh, M. Elkashlan, R. Schober, and IB. Collings, "Transmit antenna selection for security enhancement in MIMO wiretap channels," IEEE Transactions on Communications, vol. 61, no. 1, pp. 144-154, 2013.

14. BS. Tan, KH. Li, and KC. Teh, "Performance analysis of orthogonal space-time block code with minimum-selection generalized selection combining receiver over Rayleigh fading," IEEE Transactions on Vehicular Technology, vol. 61, no. 3, pp. 1463-1467, 2012.

15. V. Tarokh, H. Jafarkhani, and AR. Calderbank, "Space-time block codes from orthogonal designs," IEEE Transactions on Information Theory, vol. 45, no. 5, pp. 1456-1467, 1999.

16. SS. Ikki, and S. Aissa, "Impact of imperfect channel estimation and co-channel interference on dual-hop relaying systems," IEEE Communications Letters, vol. 16, no. 3, pp. 324-327, 2012.

17. A. Nadia, AR. Chowdhury, M. Hossain, M. Islam, and MR. Amin, "Performance evaluation of two-hop wireless link under Nakagami-m fading," International Journal of Advanced Computer Science and Applications, vol. 4, no. 7, pp. 142-146, 2013.

18. M. Elkashlan, PL. Yeoh, N. Yang, TQ. Duong, and C. Leung, "A comparison of two MIMO relaying protocols in Nakagami-m fading," IEEE Transactions on Vehicular Technology, vol. 61, no. 3, pp. 1416-1422, 2012.

19. TA. Tsiftsis, GK. Karagiannidis, PT. Mathiopoulos, and SA. Kotsopoulos, "Nonregenerative dual-hop cooperative links with selection diversity," EURASIP Journal on Wireless Communications and Networking, vol. 2006, no. 2, pp. 34-34, 2006.

20. M. Matthaiou, and C. Zhong, "Low-SNR analysis of MIMO Weibull fading channels," IEEE Communications Letters, vol. 16, no. 5, pp. 694-697, 2012.

21. S. Verdu, "Spectral efficiency in the wideband regime," IEEE Transactions on Information Theory, vol. 48, no. 6, pp. 1319-1343, 2002.

22. G. Amarasuriya, C. Tellambura, and M. Ardakani, "Performance analysis framework for transmit antenna selection strategies of cooperative MIMO AF relay networks," IEEE Transactions on Vehicular Technology, vol. 60, no. 7, pp. 3030-3044, 2011.

23. AY. Panah, and RW. Heath, "Single-user and multicast OFDM power loading with nonregenerative relaying," IEEE Transactions on Vehicular Technology, vol. 58, no. 9, pp. 4890-4902, 2009.

24. TQ. Duong, DB. Ha, HA. Tran, NS. Vo, and A. Haroon, "On the symbol error probability of distributed-Alamouti scheme," Journal of Communications, vol. 4, no. 7, pp. 437-444, 2009.

25. Y. Liu, and W. Chen, "Adaptive resource allocation for improved DF aided downlink multi-user OFDM systems," IEEE Wireless Communications Letters, vol. 1, no. 6, pp. 557-560, 2012.

26. A. Tall, Z. Rezki, and MS. Alouini, "MIMO channel capacity with full CSI at low SNR," IEEE Wireless Communications Letters, vol. 1, no. 5, pp. 488-491, 2012.

27. O. Souihli, and T. Ohtsuki, "Benefits of rich scattering in MIMO channels: a graph-theoretical perspective," IEEE Communications Letters, vol. 17, no. 1, pp. 23-26, 2013.

28. C. Zhong, T. Ratnarajah, and KK. Wong, "Outage analysis of decode-and-forward cognitive dual-hop systems with the interference constraint in Nakagami-fading channels," IEEE Transactions on Vehicular Technology, vol. 60, no. 6, pp. 2875-2879, 2011.