Bekkouch and Faraoun: Robust and Reversible Image Watermarking Scheme Using Combined DCT-DWT-SVD Transforms
Abstract
We present a secure and robust image watermarking scheme that uses combined reversible DWT-DCT-SVD transformations to increase integrity, authentication, and confidentiality. The proposed scheme uses two different kinds of watermarking images: a reversible watermark, W1, which is used for verification (ensuring integrity and authentication aspects); and a second one, W2, which is defined by a logo image that provides confidentiality. Our proposed scheme is shown to be robust, while its performances are evaluated with respect to the peak signal-to-noise ratio (PSNR), signal-to-noise ratio (SNR), normalized cross-correlation (NCC), and running time. The robustness of the scheme is also evaluated against different attacks, including a compression attack and Salt & Pepper attack.
Key words: Image Security, Image Watermarking, Reversible DWT-DCT-SVD Transform
1. Introduction
In current applications, network technologies have been highly improved so that users can gain easier access to remote facilities and send, receive, or share different types of digital data via the Internet. However, while the Internet is a useful public environment, it is not always secure for personal data transmission and exchange. Thus, important information must be manipulated to be concealed when provided via the Internet so that only the authorized receiver can get full access to it. For such reasons, several security methods have been developed in order to ensure several security aspects of digital data. These methods include encrypting, secretly sharing, and secretly hiding messages in data content to ensure several security properties, including authentication, confidentiality, and integrity.
Digital watermarking, which is the act of hiding a signal (watermark) into an image, is one of these proposed techniques that is used to protect the rights of owners. While the tremendous growth in computer networks, coupled with the exponential increase of computer performance, has facilitated the distribution of multimedia data such as images; publishers, artists, and photographers may be unwilling to distribute pictures over the Internet due to a lack of security since any images can be easily duplicated and distributed without the owner’s consent. Digital watermarks have been proposed as a way to tackle this tough issue. The use of a digital signature could discourage copyright violations and may help determine the authenticity and ownership of an image.
Watermarking techniques can be classified into two main classes according to the domain used for embedding. These classes are as follows: spatial techniques, which are implemented in a spatial domain by directly modifying pixel values; and frequency techniques, which are applied in a frequency domain when the watermark is embedded by modifying the transform domain coefficients that are carried out after a given decomposition, such as discrete cosine transform (DCT) [ 1, 2], discrete wavelet transform (DWT) [ 2, 3], discrete Fourier transform (DFT) [ 4], or singular value decomposition (SVD) as used in [ 5, 6]. The two main properties that a watermarking technique must provide in order to be effective are imperceptibility and robustness. The former implies that an embedded mark should be perceptually invisible to assure the best image quality after the embedding step, while the latter property is satisfied if the inserted mark is difficult to remove and can be recovered even if the image is modified or altered by a certain type of attack (image modification and manipulation). More precisely, Cox et al. [ 7] defined robustness as the ability to detect a watermark after any kind of modifying operation is performed. The more I amount of inserted information increases in the image, the more the signature is visible or perceptible and therefore, the robustness decreases. In addition, a watermarking system can be either reversible or irreversible. A reversible watermarking system can extract or restore the original data from the watermarked image by applying an inverse transformation without producing any changes and it avoids all possibly created irreversible distortion of the original image. In contrast, by using irreversible watermarking, there is no way to extract the original image from the watermarked image [ 8]. In this paper, our aim is to propose a reversible watermarking algorithm using a combination of the three transforms, which are as follows: the DWT transform, the DCT transform, and the SVD transform. Even if each one has already been used individually to build watermarking systems, combining them allows them the best robustness and to benefit from the advantages of several transformations. The proposed scheme is based on the insertion of two different marks, W1 and W2, in the three different domains of DWT, DCT, and SVD.
The remaining of the paper is organized as follows: Section 1 presents an introduction to watermarking systems, Section 2 discusses related works, and Section 3 presents the proposed technique. In Section 4, experimental results are presented, in which the performances of the proposed method are evaluated and compared to some of the existing ones according to PSNR, the NCC coefficient of the correlation between the original watermark and extracted watermark, SNR, and elapsed time. We also evaluate the robustness of the watermarking scheme with respect to a salt & pepper noise attack, a Gaussian noise attack, and a JPEG compression attack. Finally, conclusions are presented in Section 5.
2. Related Works
The transform domain obtained when applying a DCT to the host image is similar to the DFT that allows an image to be divided into the following different frequency bands: high, middle, and low frequency bands. The technique, which is based on DCT, has the important advantage of providing robust compression operations with reduced computation overhead. In their proposed scheme, Cox et al. [ 9] applied the DCT to the host image at a low frequency and then modified the n coefficients belonging to the highest amplitude of the transform to insert the watermarking data. In this work, the original image is required to extract the watermark. In [ 10], the authors describe the same principle for the embedding process but the extraction of the watermark is performed using a correlation approach without the need for an original image. Recently, others have proposed many other watermarking DCT-based schemes, which are as follows: in [ 11] using columns transforms, in [ 12] using selected pixel regions, and in [ 13] using visual cryptography. The DWT transform is a modern mathematical tool that has been widely studied in signal processing in general and, in particular, in image compression. This transform is based on separating the original image into the following four non-overlapping multi-resolution subbands: lower resolution approximation image (LL), horizontal high frequency band (HL), vertical high frequency band (LH), and diagonal high frequency band (HH). In general, most of the image energy is situated at the lower frequency subbands (LL) and therefore, hiding watermarks in the lower frequency subbands (LL) may degrade the quality of the host image even if it could significantly increase the robustness. Tao and Eskicioglu [ 14] proposed a watermarking technique that is based on the insertion of the watermark as a binary logo in the four subbands. The quality of the extract watermark is determined by the similarity rate. Recent works using the DWT for watermarking include the scheme in [ 15] that used chirp z-transform and [ 16], which uses self-adaptive differential evolution. The SVD transformation is another mathematical tool used in digital image processing. Recently, this transform has been used for watermarking because of its algebraic proprieties. It is generally used to compute two orthogonal matrices, U and V, and the diagonal matrix of S [ 17]. In [ 18], the author computed the SVD of both the original image and the watermark image (logo) and then added singular values of the watermark images to those of the host image where the watermark W is added to the matrix S. Then, a new SVD process is performed on the new matrix: D = S + k*W, to get U w, S w, and V w, where, k is a scale factor that controls the strength of the watermark embedded into the original image. The watermarked image I w is then obtained by multiplying the matrices U, S W, and V. Many recent works that use the SVD transform to build watermarking systems can be found in [ 19– 21].
3. The Proposed Watermarking Scheme
Watermarking schemes that use the frequency domain as a workspace are advantageous for compression operations since the same domain is used to encode the image, and hence, provides a faster processing time. In the proposed scheme, a combination of the three frequency transforms DCT, DWT, and SVD is used to achieve optimal robustness. The DWT transformation is first used to decompose the image into the four subbands, namely LL, LH, HL, and HH, which are described above. The watermark images are then embedded on the HL detail of the host image and the DCT is applied on LL and HH to produces D and D3 that will undergo each one the SVD transforms to give them the following three matrices, respectively: diagonal S and S3 and the two orthogonal ones U, V for D and U3,V3 for D3.
The first step of embedding consists in generating both the watermarks W1 and W2. A transformed DWT is applied to the two watermarks producing four levels (LL1, HL1, LH1, HH1) and (LL2, HL2, LH2, HH2) for W1 and W2, respectively. We then perform the DCT transform on LH1 and LH2 to give D2 and D1, and the SVD transform is applied to D2 and D1 to give (U2, S2, V2) and (U1, S1, V1), respectively. The embedding of the watermark W1 is performed by adding the two diagonals matrices S and S2 that were previously multiplied by a factor α to obtain S33. Embedding the watermark W2 is performed by adding the two diagonals matrices S and S2 that were multiplied by the same factor α to obtain S32. The SVD is performed on S32 to obtain Wimg, in order to reconstruct the watermarked image IW and the inverse IDCT is applied to Wimg.
In the following sections, we present the detailed steps for the embedding and extraction process of the proposed watermarking approach, which uses the DCT, DWT and the SVD transformations in a unique scheme. The performances of the proposed approach are evaluated in the next section.
3.1 Watermark Embedding Process
In order to ensure the main aspects of security, which are authenticity, integrity, and confidentiality, we propose the use of a new hybrid reversible watermarking approach that performs the embedding of two different kinds of watermarks:
- A reversible watermark W1, which is used to verify data authentication and the integrity of the image. It is defined by the RSA enciphering of a data block composed of a combination of the SHA-512 hash of the most significant bits (MSB) with the RLE compression of the least significant bits (LSB); - A second watermark W2 is created by enciphering the inputted logo using a secret key that allows the image’s user to check its confidentiality and integrity. It also transforms the result using DWT and SVD transforms.
The proposed watermarking process takes the cover image I as input and the two generated watermarks, W 1 and W 2, to give the watermarked image I w as output. Details of different embedding and watermark extraction steps are presented in the following sections, while a complete diagram of the approach is illustrated in Figs. 1 and 2. The matrix S1 representing the watermark W1 is generated according to the following steps:
Extracting the MSB from the cover image and calculating the corresponding message authentication code (MAC) using the SHA-512 algorithm; Concatenating the obtained MAC with the patient information and encrypting the resulting string(as shown in Fig. 3); Selecting the LSBs of all pixels and compressing the resulting string using RLE; Concatenating the compressed string and the encrypted one; Converting the characters of a string to a binary matrix A; Applying the DWT on the resulting matrix A to obtain: LL1, HL1, LH1, and HH1; Applying the DCT transform on LH1 to obtain a new matrix D1; Performing the SVD on D1 to obtain the SVs decomposition of: U1.S1.V1′.
The obtained matrix S 1 represents the watermark W 1 that is to be inserted as the watermarking information in the host image I. The watermark W 1 is computed from the host image and will serve for integrity verification and authentication (as illustrated in Fig. 3). The matrix S2, which represents the watermark W2, is then generated according to the following steps:
Reading the watermark message and reshaping it into a vector; A pseudorandom sequence is then generated from the secret key using a stream ciphering algorithm (RC4 in our implementation) and combined using XOR with a watermark message; Applying the DWT transform on the resulting ciphertext after reshaping it as a matrix to obtain: LL2, HL2, LH2 and HH2; Applying the DCT to the sub-band LH2 to obtain the new matrix D2; Decompose D2 in singular values to obtain the SVs: SVD (D2)=U2.S2.V2t.
The obtained matrix S 2 represents the watermark W 2 that is to be inserted as the watermarking information in the host image I. The watermark W 2 is computed from the host image and will serve for confidentiality guaranteeing (as illustrated in Fig. 4). After generating the two watermarks W1 and W2, the embedding phase can now be performed. The embedding process for the watermark W1 is first performed as follows:
Applying the DWT transform to decompose the cover image into four sub-bands; Perform the SVD on the subband LL to obtain the SVs: SVD(LL) = U.S.V′; Insert the singular values of the watermark S1 in the matrix S of LL to obtain: S33 = S + α* S1; Perform the SVD on S33 to obtain the SVs: SVD(S33) = U6.S6.V6t; Finally, calculate the watermarked matrix using U, V, and S6: Wimg2 = U . S 6 . Vt.
After that, the watermark W2 is embedded into the watermarked image using the following steps:
Apply the DCT to subband HH of the cover image to get the new matrix D3; Perform the SVD on D3: SVD (D3)=U3.S3.V3t; Add the content of S2 of the watermark W2 to the matrix diagonal S3: S32= S3+ α . S2; Perform the SVD on S32 to obtain U5, V5t, S5 and reconstruct the Wimg matrix using S5, U3 and V3: Wimg = U3. S5.V3t. Apply the inverse DCT to reconstruct B1 using Wimg; Obtain the watermarked image IW by performing the inverse DWT using B2 and three sets of DWT coefficients: HL2, B1 and HH2.
The detailed process of watermark embedding is illustrated in Fig. 1.
3.2 Watermark Extraction Process
The extraction phase includes extraction of watermark W1 and watermark W2. The first step consists of applying the decomposition DWT to decompose the watermarked image IW, which produce four detailed components: LLw*, HLw*, LHw*, and HHw* (these are possibly corrupted). The detail LLw* is used for extracting watermark W1, while the HHw* is used for extracting watermark W2.
The SVD transform is applied to LLw* to give the three matrixes Uw*, Sw*, and Vw*. After that, the matrix Sr is computed using the diagonal matrix S (obtained during the SVD transformation applied on the original detail LL of the original image) and the matrixes SW. A new matrix D* is then computed using the matrixes U1 and V1 that were obtained during the embedding process, and the inverse DCT transform is applied to the new matrix D* to produce a matrix G. Finally, in order to extract the watermark W1, the inverse DWT transform of the original image’s details LL1, LH1, HL1, and G are computed.
In order to extract the second watermark W2, the DCT transform is applied to HHw* producing TW. The SVD transform is then applied to TW produce three matrixes: Uww, Vww, and Sww. These are used with the original matrix S3 to compute the matrix Sr1. A new matrix D22* is then computed using the matrix Sr1 matrixes with the matrixes U2, V2 of the original watermark W2. Finally, applying the inverse DCT on the new matrix D22* gives the new matrix B, and the inverse DWT of the original detail LL2, HL2, LH2, and B is computed and deciphered using the same secret key used during the watermark generation to deduce the watermark W2. The different steps for extracting watermark W1 are explicitly explained as follows:
The watermarked image Iw* (possibly attacked) is decomposed into four DWT transform coefficients: LLw*, HLw*, LHw*, and HHw*; The SVD transform is performed on LLw* to obtain: SVD(LLw*) = Uw*.Sw*.Vw*t; The corrupted watermark is obtained by: Sr = (S−Sw*)/4; The matrix containing the watermark is computed by: D* = U1.Sr.V1t; The extracted watermark W1* is obtained by performing the inverse DWT using the original watermark’s coefficient sets: LL1, HL1, LH1, and D*.
The different steps for extracting watermark W2 are explicitly explained as follows:
The DCT transform is applied to HHw*to obtain Tw; The SVD transform is applied to Tw to obtain: SVD(Tw ) = Uww . Sww .Vwwt ; The corrupted watermark is obtained by: Sr1 = (S3−Sww )/4; The matrix containing the watermark is computed by: D22* = U2 . Sr1. V2t; The inverse DCT transform is applied to D22*; The extracted watermark W2* is obtained by performing the inverse DWT using the original watermark’s W2 coefficient set: LL2, HL2, LH2, and D22*.
The detailed process of watermark extraction is illustrated in Fig. 2.
3. Experiments and Obtained Results
The performances of the proposed method were analyzed using the metric normalized cross-correlation (NCC), which expressed the quality of the extracted watermark be measuring the similarity between the original watermarks W and the extracted watermarks W*. According to [ 22], the NCC is defined by Eq. (1), where W (i, j) is the pixel values at the position (i, j) of the original image, and W*(i, j) is the pixel values at the position (i, j) of the watermarked image. The peak signal-to-noise ratio (PSNR) and signal-to-noise ratio (SNR) [ 23] between the original image and watermarked image are defined as shown below: where, M and N are the height and width of the image. I is the original image and IW is the watermarked image. Images having high PSNR and SNR values are preferable.
In order to evaluate the proposed scheme, we used three 256×256 gray scale medical images: IRM_31, IRM_32, and IRM_33 (illustrated in Fig. 5(a), (b), and (c)). The watermark image W 1 has a size of 1×206 and the watermark image W 2 has a size of 106×143 binary pixels. Both of which are illustrated in Fig. 6. Fig. 7 shows the results of when the watermarking process is applied to the original image. To investigate the robustness of the scheme with respect to common watermarking attacks, we attacked the watermarked image by applying a JPEG compression (with a quality factor equal to 10%), a salt & pepper noise attack (with a quality factor 0.006), and a rotations of 90°, 180°, and 270° respectively. Fig. 8 illustrates the different attacked watermarked images that correspond to the original IRM_31 one. Table 1 illustrates the obtained performances results measured in terms of NCC metrics. The measure was applied between the originally inserted watermark and the one extracted from the watermarked images after applying a given attack. The result shows that even with a significant attack that destroys some of the content of the image, the watermark can still be recovered with a very satisfactory quality. For further illustration, Fig. 9 shows the watermark W 1 that was extracted from several attacked images. It is clear that the perceptual quality of the watermark is highly preserved even with hard attacks, such as compression and cropping. Further experiments have been conducted in order to show the robustness of the proposed scheme with respect to several attacks. For attacked watermarked images, we calculated a detection score value that indicated if the watermark is really present or not in the images. We implemented an experiment inspired from [ 25] using a traditional NCC between the original watermark and the decoded watermark. The score is computed as follows: where, pi and
pi′ are elements of the original and the extracted watermarks, respectively, and M is the size of the watermark.
If the score S is higher than a certain threshold Ts, we can say that the watermark is present in the image. According to [ 25], the threshold value can be computed using the following formula: Hence, since the size of the watermark W 1 is 106×143 binary pixels, we concluded that the threshold Ts is equal to 0.14. In Fig. 10, we show the variation between different detection score that were obtained for the extracted watermark from several attacked images by varying the angle of rotation. We can easily see that the detection score is always higher than the threshold Ts. This means that the watermark was always detected. An Addition computation of the detection score was performed with respect to the JPEG compression attack. Fig. 11 illustrates the evolution of the watermark’s detection score with respect to several values of compression ratios. We see that even with high compression rates (raising very degraded image quality and information loss), the watermark can still be detected since the detection score is above the threshold Ts. The results of Figs. 10 and 11 approve the NCC results given in Table 2, and they ensure that the proposed scheme is very robust against several types of watermarking attacks.
5. Conclusions
In this paper, we present a novel watermarking scheme using a combination of reversible DWT/DCT/SVD transformations in order to insert two different types of watermarks into a digital image. The aim of the scheme is to increase the security of a data hiding mechanism, which can be applied in both copyright protection and content authentication domains. The three transformations that we used operated in the transformed frequency domain of the image.
Even though we obtained satisfying results, the reversible DWT-DCT-SVD based method offers better capacity and imperceptibility properties than the classical DWT-DCT-SVD approach proposed in [ 24], while the obtained results show that our proposed scheme can resist several types of image watermarking attacks, including geometric transformation attacks, noises attacks, and JPEG compression attacks. In our future work, we intend to extend the scheme for color image watermarking by inserting the two different watermark images into the RGB color plans.
Biography
Souad Bekkouche
She was born in 1981. She is teaching computer science at the computer science department of Mascara’s university-Algeria. She prepare actually his Ph.D. thesis about images watermarking and security. Research Interests are image watermarking and encryption techniques.
Biography
Kamel Mohamed Faraoun
He received his master’s degree in computer science at the computer science department of Djillali Liabes University, Sidi-Bel-Abbès, Algeria in 2002, his Ph.D. degree in computer science in 2006, and his HDR degree in computer science and intelligent systems in 2009 from UDL-University. His research areas include computer security, cryptography, cellular automata, evolutionary programming and information theory.
References
1. YP. Xu, and LQ. Jia, "Research of a digital watermarking algorithm based on discrete cosine transform," in Proceedings of the 3rd International Symposium on Electronic Commerce and Security Workshops (ISECS’10), Guangzhou, China, 2010, pp. 373-375.
2. CM. Pun, and IT. Lam, "Fingerprint watermark embedding by discrete cosine transform for copyright ownership authentication," International Journal of Communications, vol. 3, no. 1, pp. 17-24, 2009.
3. YI. Khamlichi, M. Machkour, K. Afdel, and A. Moudden, "Medical image watermarked by simultaneous moment invariants and content-based for privacy and tamper detection," in Proceedings of the 6th WSEAS International Conference on Multimedia Systems & Signal Processing, Hangzhou, China, 2006, pp. 16-18.
4. PK. Dhar, MI. Khan, and JM. Kim, "A new audio watermarking system using discrete Fourier transform for copyright protection," International Journal of Computer Science and Network Security, vol. 10, no. 6, pp. 35-40, 2010.
5. CC. Chang, P. Tsai, and CC. Lin, "SVD-based digital image watermarking scheme," Pattern Recognition Letters, vol. 26, no. 10, pp. 1577-1586, 2005.  6. H. Demirel, C. Ozcinar, and G. Anbarjafari, "Satellite image contrast enhancement using discrete wavelet transform and singular value decomposition," IEEE Geoscience and Remote Sensing Letters, vol. 7, no. 2, pp. 333-337, 2010.  7. IJ. Cox, ML. Miller, and JA. Bloom, in Digital Watermarking, San Francisco, CA: Morgan Kaufmann Publishers, 2001.
8. OM. Al-Qershi, and BE. Khoo, "Authentication and data hiding using a reversible ROI-based watermarking scheme for DICOM images," Proceedings of World Academy of Science, Engineering and Technology, vol. 38, pp. 829-834, 2009.
9. IJ. Cox, J. Kilian, FT. Leighton, and T. Shamoon, "Secure spread spectrum watermarking for multimedia," IEEE Transactions on Image Processing, vol. 6, no. 12, pp. 1673-1687, 1997.  10. A. Piva, M. Barni, F. Bartolini, and V. Cappellini, "DCT-based watermark recovering without resorting to the uncorrupted original image," in Proceedings of International Conference on Image Processing, Santa Barbara, CA, 1997, pp. 520-523.  11. DH. Kekre, DT. Sarode, and S. Natu, "Robust watermarking scheme using column DCT wavelet transform under various attacks," International Journal on Computer Science and Engineering, vol. 6, no. 1, pp. 31-41, 2014.
12. J. Abraham, and V. Paul, "Image watermarking using DCT in selected pixel regions," in Proceedings of 2014 International Conference on Control, Instrumentation, Communication and Computational Technologies (ICCICCT), Kanyakumari, India, 2014, pp. 398-402.  13. Y. Han, W. He, S. Ji, and Q. Luo, "A digital watermarking algorithm of color image based on visual cryptography and discrete cosine transform," in Proceedings of 2014 Ninth International Conference on P2P, Parallel, Grid, Cloud and Internet Computing (3PGCIC), Guangdong, China, 2014, pp. 525-530.  14. P. Tao, and AM. Eskicioglu, "A robust multiple watermarking scheme in the discrete wavelet transform domain," in Internet Multimedia Management Systems V, Bellingham, WA: International Society for Optical Engineering, 2004, pp. 133-144.  15. M. Agoyi, E. Çelebi, and G. Anbarjafari, "A watermarking algorithm based on chirp z-transform, discrete wavelet transform, and singular value decomposition," Signal, Image and Video Processing, vol. 9, no. 3, pp. 735-745, 2015.  16. M. Ali, and CW. Ahn, "An optimized watermarking technique based on self-adaptive DE in DWT–SVD transform domain," Signal Processing, vol. 94, pp. 545-556, 2014.  17. R. Liu, and T. Tan, "An SVD-based watermarking scheme for protecting rightful ownership," IEEE Transactions on Multimedia, vol. 4, no. 1, pp. 121-128, 2002.  18. DS. Chandra, "Digital image watermarking using singular value decomposition," in Proceedings of the 45th Midwest Symposium on Circuits and Systems (MWSCAS-2002), Tulsa, Oklahoma, 2002, pp. 264-267.  19. YR. Rao, E. Nagabhooshanam, and N. Prathapani, "Robust video watermarking algorithms based on SVD transform," in Proceedings of 2014 International Conference on Information Communication and Embedded Systems (ICICES), Chennai, India, 2014, pp. 1-5.  20. K. Meenakshi, CS. Rao, and KS. Prasad, "A robust watermarking scheme based Walsh-Hadamard transform and SVD using ZIG ZAG scanning," in Proceedings of 2014 International Conference on Information Technology (ICIT), Bhubaneswar, India, 2014, pp. 167-172.  21. H. Shi, F. Lv, and Y. Cao, "A blind watermarking technique for color image based on SVD with circulation," Journal of Software, vol. 9, no. 7, pp. 1749-1756, 2014.  22. MS. Hsieh, "Wavelet-based image watermarking and compression,"doctoral dissertation, Institute of Computer Science and Information Engineering, National Central University; Taiwan: 2001.
23. B. Aiazzi, L. Alparone, and S. Baronti, "Near-lossless compression of 3-D optical data," IEEE Transactions on Geoscience and Remote Sensing, vol. 39, no. 11, pp. 2547-2557, 2001.  24. M. Awasthi, and H. Lodhi, "Robust image watermarking based on discrete wavelet transform, discrete cosine transform & singular value decomposition," Advance in Electronic and Electric Engineering, vol. 3, no. 8, pp. 971-976, 2013.
25. FK. Mohamed, and R. Abbes, "RST Robust watermarking schema based on image normalization and DCT decomposition," Malaysian Journal of Computer Science, vol. 20, no. 1, pp. 77-90, 2007.
Fig. 1
Global pictorial diagram of the watermark embedding process. DWT=discrete wavelet transform, DCT=discrete cosine transform, SVD=singular value decomposition, LL=lower resolution approximation image, HL=horizontal high frequency band, LH=vertical high frequency band, HH=diagonal high frequency band. 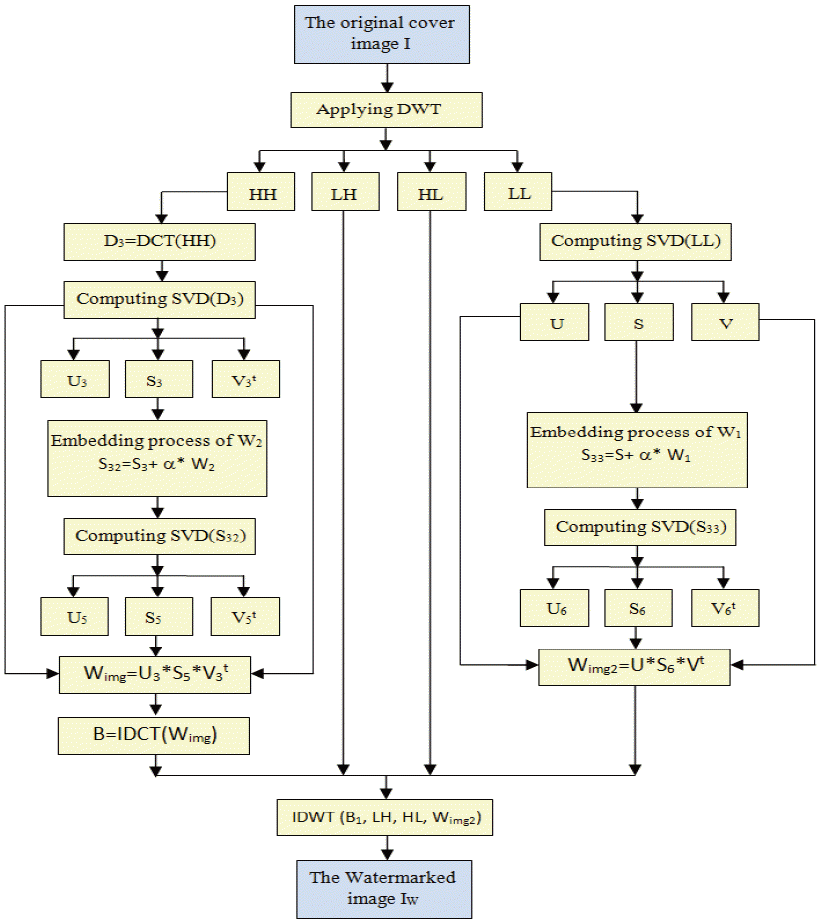
Fig. 2
Global pictorial diagram of the watermark extraction process. DWT=discrete wavelet transform, DCT=discrete cosine transform, SVD=singular value decomposition, LL=lower resolution approximation image, HL=horizontal high frequency band, LH=vertical high frequency band, HH=diagonal high frequency band. 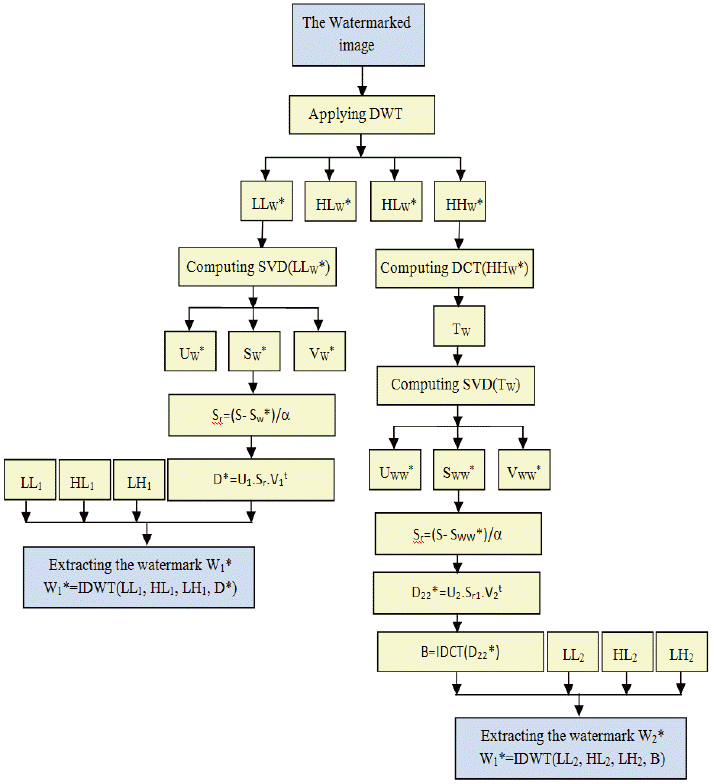
Fig. 3
Pictorial diagram of the watermark W1 generation process. MSB=most significant bits, DWT=discrete wavelet transform, DCT=discrete cosine transform, SVD=singular value decomposition, LL=lower resolution approximation image, HL=horizontal high frequency band, LH=vertical high frequency band, HH=diagonal high frequency band. 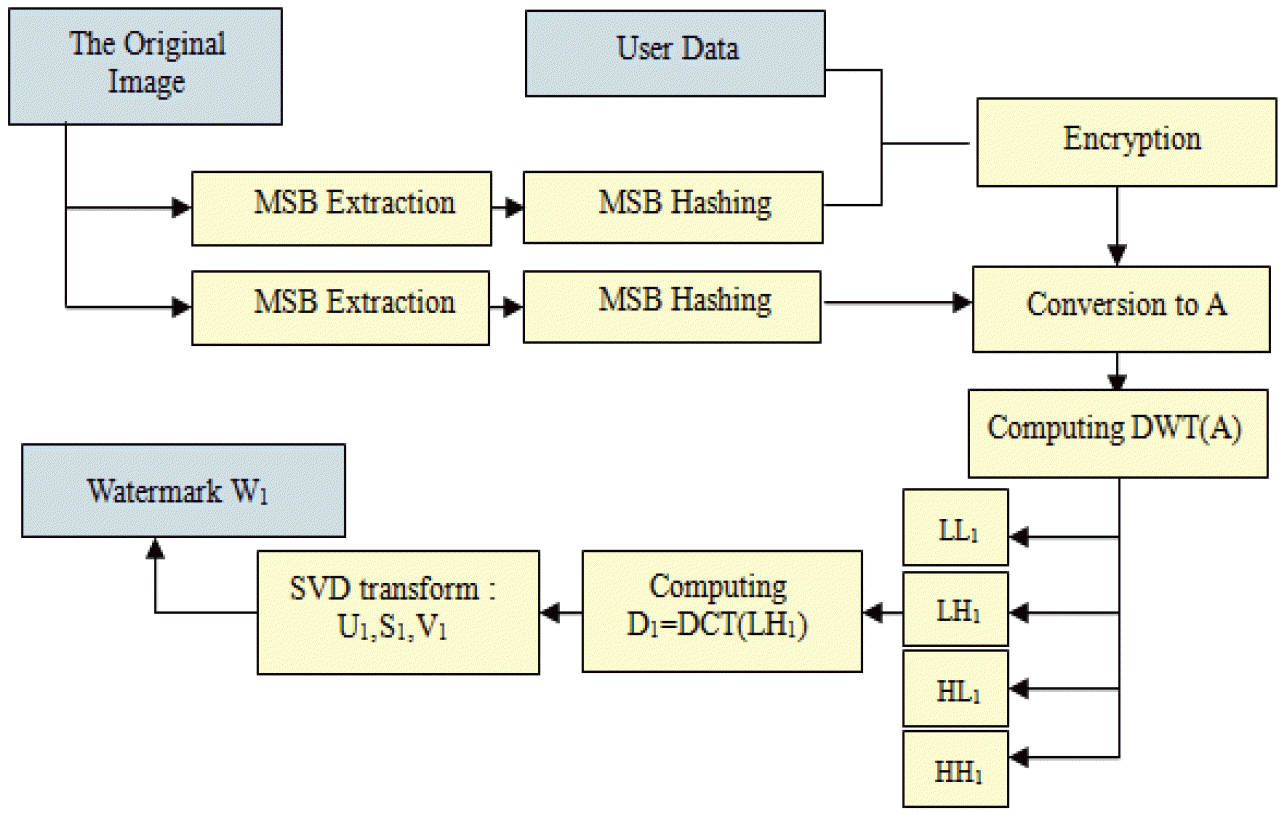
Fig. 4
Pictorial diagram of the watermark W2 generation process. DWT=discrete wavelet transform, DCT=discrete cosine transform, SVD=singular value decomposition, LL=lower resolution approximation image, HL=horizontal high frequency band, LH=vertical high frequency band, HH=diagonal high frequency band. 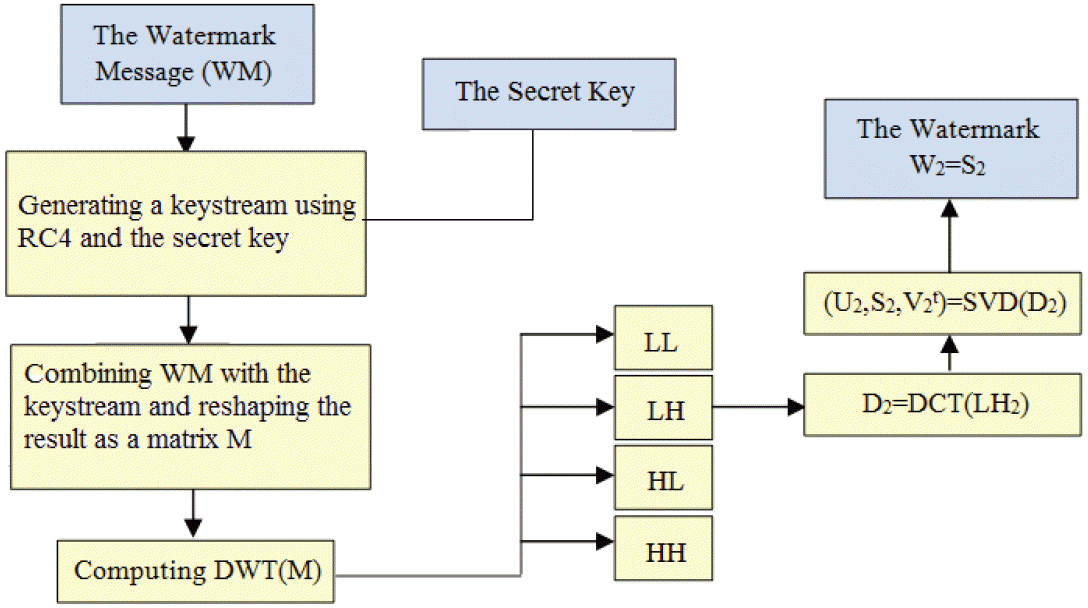
Fig. 5
Original image: (a) IRM_31, (b) IRM_32, and (c) IRM_33. 
Fig. 6
Used watermarks : (a) watermark W1 and (b) watermark W2. 
Fig. 7
Watermarked images: (a) W_IRM_31, (b) W_IRM_32, and (c) W_IRM_33. 
Fig. 8
Attacked watermarked images corresponding to IRM_31: (a) rotation 90°, (b) rotation 180°, (c) rotation 270°, (d) cropping, (e) JPEG compression, and (f) salt & pepper noise. 
Fig. 9
Extracted watermark from attacked images : (a) rotation 90°, (b) rotation 180°, (c) rotation 270°, (d) cropping, (e) salt & pepper and (f) JPEG compression. 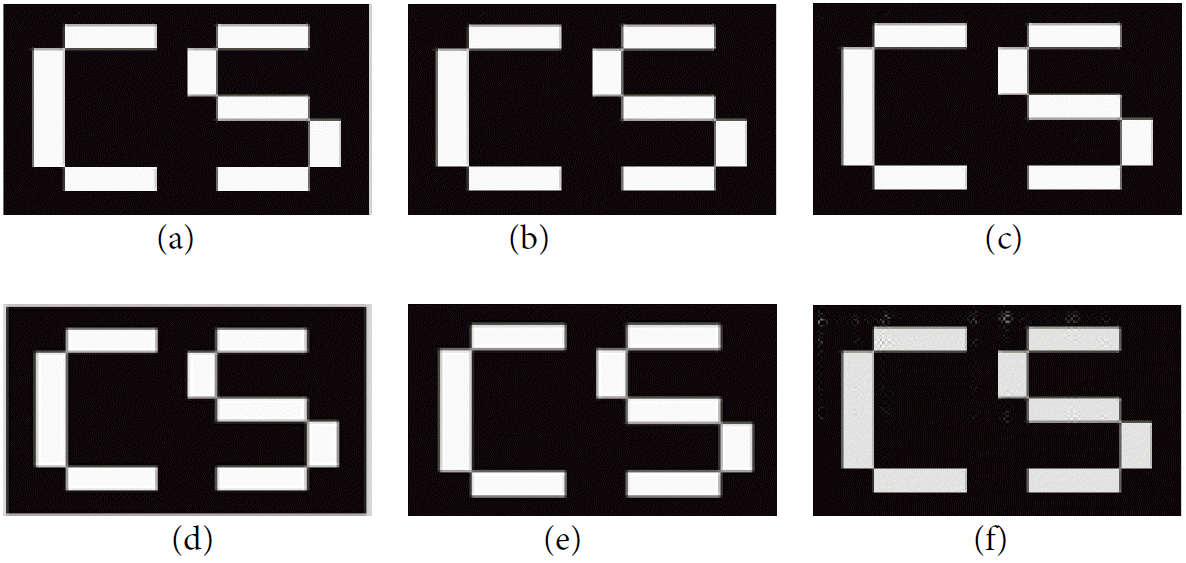
Fig. 10
Obtained watermark’s detection scores when varying the angle of the rotation attack on the watermarked image. 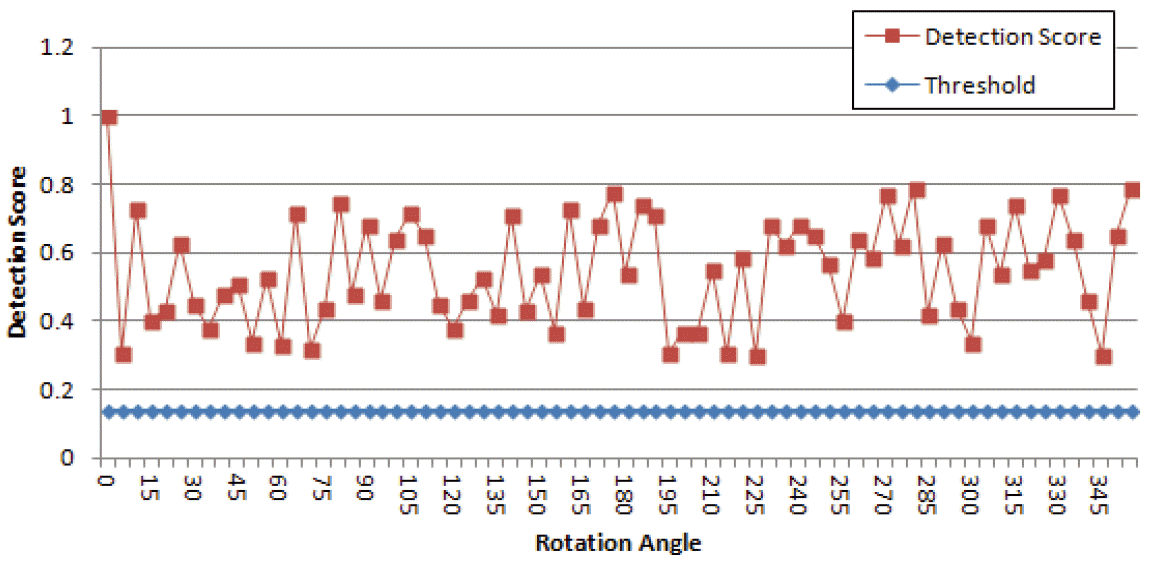
Fig. 11
Obtained watermark’s detection scores when varying the JPEG compression ratio of the watermarked image. 
Table 1
Performances result of the proposed scheme compared to the approach in [ 24]
|
Approach proposed in [24] |
Proposed method |
|
PSNR |
SNR |
NCC |
Run time |
PSNR |
SNR |
NCC1 |
NCC2 |
Run time |
|
IRM_31 |
36.246 |
20.176 |
0.999 |
8.42 |
44.012 |
27.939 |
0.996 |
0.999 |
23.665 |
|
IRM_32 |
36.404 |
19.619 |
0.999 |
8.72 |
45.587 |
28.802 |
0.998 |
0.997 |
21.574 |
|
IRM_33 |
35.612 |
21.855 |
0.999 |
8.81 |
47.309 |
33.552 |
0.998 |
0.998 |
25.818 |
Table 2
Performances comparison with respect to NCC measure of the proposed watermarking scheme and the one proposed in [ 24] under several attack
|
|
Rotation (90°) |
Rotation (180°) |
Rotation (270°) |
JPEG compression |
Cropping |
Salt & pepper |
|
IRM_31 |
|
NCC obtained in [24] |
0.99971 |
0.99972 |
0.99972 |
0.99971 |
0.99976 |
0.99982 |
|
Proposed |
NCC1
|
0.99959 |
0.99959 |
0.99940 |
0.99890 |
0.98698 |
0.97374 |
|
NCC2
|
0.99988 |
0.99988 |
0.99989 |
0.99989 |
0.99988 |
0.99773 |
|
|
IRM_32 |
|
NCC obtained in [24] |
0.99970 |
0.99970 |
0.99970 |
0.99967 |
0.99973 |
0.99990 |
|
Proposed |
NCC1
|
0.99896 |
0.99896 |
0.99896 |
0.99810 |
0.96386 |
0.97184 |
|
NCC2
|
0.99988 |
0.99988 |
0.99988 |
0.99989 |
0.99988 |
0.99768 |
|
|
IRM_33 |
|
NCC obtained in [24] |
0.99953 |
0.99953 |
0.99953 |
0.99959 |
0.99965 |
0.99994 |
|
Proposed |
NCC1
|
0.99925 |
0.99931 |
0.99925 |
0.99861 |
0.98877 |
0.98792 |
|
NCC2
|
0.99988 |
0.99988 |
0.99987 |
0.99989 |
0.99988 |
0.99807 |
|












