|
|
Abstract
Generally, the wireless network provides priority to handover calls instead of new calls to maintain its quality of service (QoS). Because of this QoS provisioning, a call admission control (CAC) scheme is essential for the suitable management of limited radio resources of wireless networks to uphold different factors, such as new call blocking probability, handover call dropping probability, channel utilization, etc. Designing an optimal CAC scheme is still a challenging task due to having a number of considerable factors, such as new call blocking probability, handover call dropping probability, channel utilization, traffic rate, etc. Among existing CAC schemes such as, fixed guard band (FGB), fractional guard channel (FGC), limited fractional channel (LFC), and Uniform Fractional Channel (UFC), the LFC scheme is optimal considering the new call blocking and handover call dropping probability. However, this scheme does not consider channel utilization. In this paper, a CAC scheme, which is termed by a uniform fractional band (UFB) to overcome the limitations of existing schemes, is proposed. This scheme is oriented by priority and non-priority guard channels with a set of fractional channels instead of fractionizing the total channels like FGC and UFC schemes. These fractional channels in the UFB scheme accept new calls with a predefined uniform acceptance factor and assist the network in utilizing more channels. The mathematical models, operational benefits, and the limitations of existing CAC schemes are also discussed. Subsequently, we prepared a comparative study between the existing and proposed scheme in terms of the aforementioned QoS related factors. The numerical results we have obtained so far show that the proposed UFB scheme is an optimal CAC scheme in terms of QoS and resource utilization as compared to the existing schemes.
Cellular communication is one of the favored ways for conducting worldwide communication. Throughout the world, the amount of cellular system users is drastically increasing day by day. Due to the incremental demand of the cellular networks, there has been tremendous interest and progress in this field. The cellular network provides its services by dividing its physical area into different specific regions, which are called cells. When a mobile user crosses the cell boundary or the quality of the wireless link between the mobile station and base station is unacceptable, the process of a handover call is then initiated [1]. In recent years, a remarkable tendency to design the cellular network is (i) decreasing the cell size and (ii) increasing user mobility [2]. These two factors result in more frequent handovers. In practice, it has been observed that users are more sensitive to the dropping of an ongoing or handed over call than the blocking of a new call [3]. Therefore, a proper management of channel allocation is necessary for this kind of provisional service.
A call admission control (CAC) scheme is a provisional technique that provides the quality of service (QoS) to the different calls at the target level by limiting the number of enduring calls in the system [4]. One major challenge in designing a CAC scheme arises to provide service two major types of calls: new calls and handover calls. The QoS performances are generally measured by new call blocking probability (CBP) and handover call dropping probability (CDP). Since blocking a new call is less serious than dropping a handover call, CAC schemes usually give a higher priority to handover calls. Furthermore, optimum resource utilization (channel utilization) is also a very important issue from the service provider’s point of view in designing a CAC scheme because the resource of a wireless system is limited.
There are a number of CAC schemes [1–11] where the authors consider the different parameters to analyze the performance of their proposed schemes. A very general and easiest CAC scheme is a fixed guard band (FGB) or guard channel scheme by which the QoS, in terms of new CBP and handover CDP, can be easily achieved. However, the scheme cannot assure the proper channel utilization [5] for reserving some channels for only handover calls. A fractional guard channel (FGC) scheme or thinning scheme-I and limited fractional channel (LFC) scheme are proposed in [6]. In the FGC scheme, new calls are accepted by the channels depending on the channel occupancy where new CBP and handover CDP intensify excessively with the increased traffic rate. This is the limitation of the FGC scheme in reaching the proper QoS. The LFC is proposed for optimum QoS compared to the FGB and FGC schemes in terms of new CBP and handover CDP. However, channel utilization by LFC is not well thought out as the scheme handover and new calls are considered to be a constant ratio, which is its very important limitation. According to the thinning scheme-II [7,8] new calls are accepted by different channels depending on the traffic arrival rate. This scheme can achieve QoS by blocking a number of new calls after a threshold value, so it cannot assure the optimum channel utilization. A uniform fractional channel (UFC) scheme is proposed in [9–11]. The authors of these papers conclude that the UFC scheme is better in traffic where the handover to a new call ratio is very low. However, this conditional approach is not realistic.
In this paper, we propose a CAC scheme where we hybridize the idea of a non-priority scheme (NPS) [12], UFC scheme, and priority scheme. Since this scheme is a combination of NPS, UFC, and a priority scheme, the main contribution of this work is that it develops a proper mathematical modeling of this scheme. As far as we know, this kind of CAC scheme has not ever been proposed before. We call this scheme a uniform fractional band (UFB) scheme. This scheme divides the total channels into three bands. In the first band, the new and handover calls will get access with a uniform acceptance factor of 1 and this band shows the non-priority characteristic. In the second band, the channels with a fractional acceptance factor accept the new calls and the handover calls are accepted with an acceptance factor of 1. This band or set of channels that have the characteristics of the UFC scheme, which helps the scheme to utilize more channels and provides fractional priority to the handover calls. In the third band, the new calls will be completely blocked, which means that these channels are reserved only for handover calls and therefore, this set of channels provide the integral priority to handover calls. Based on this idea, handover calls get priority by two bands, where in the FGB scheme, there is only one band where handover calls get priority.
Regarding the notion of UFB, there is the apprehension of the handover CDP increasing for lessening the new CBP. To overcome this obstacle, it is necessary to determine the proper value of the acceptance factor and to choose the number of channels of the middle band. The UFB scheme ensures more channel utilization than the FGC, FGB, and UFC schemes maintaining the QoS, which proves that the UFB scheme can handle more traffic of wireless cellular networks than the others by ensuring the conditions of QoS.
Another contribution of this paper is the characterization of the mathematical models of several conventional CAC schemes by identical technique with the appropriate algorithm. We scrutinized the conventional CAC schemes by considering the handover call rate as a linear function of the new call arrival rate. However, in practice, the handover call rate in a system cannot maintain a fixed ratio with new calls [12]. Basically, handover call rate estimation is deliberated by a statistical hypothesis, which is revealed in the next section of this paper. We also distinguished the results of the fixed ratio handover call and the statistical handover rate by appropriate numerical analysis.
The paper is organized as follows: Section 2 provides our hypothesis on handover and new call ratio. Existing and more popular guard channel schemes are explained in Section 3. In Section 4, we extensively discuss our proposed scheme. The numerical performances of this paper are analyzed in Section 5. Finally, we conclude our total numerical observations in Section 6.
In cellular networks, the rate of new calls and handover calls does not maintain a linear ratio. That is why a hypothesis is necessary to obtain the relationship between them. The relationship amongst the new call arrival rate (λn), the handover call arrival rate (λh), and the average channel departure rate (μ) is essential for determining the new CBP and handover CDP. Here, it is considered that PB and PD represent the new CBP and handover CDP, respectively. The call arriving processes are considered as Poisson’s distribution. A new call that arrives in the system may be either completed within the original cell or handed over to another cell before completing the call. The probability of a call being handed over depends on two factors: (i) the average dwell time (1/η) and (ii) the average call duration (1/μ). Both the average call duration and the cell dwell time are assumed to be exponential [2,13]. The handover probability, Ph, of a call at a particular time is given by:
Furthermore, the handover call arrival rate into a cell is evaluated as:
The equation agrees from balancing the rates of handover calls into and out of a cell.
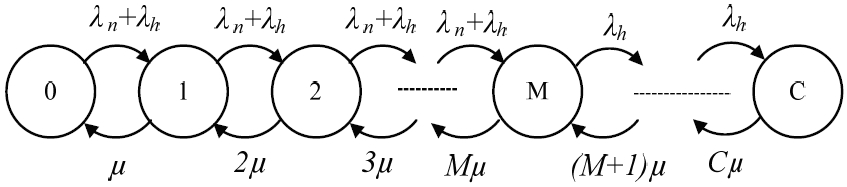
A FGB scheme is a general priority scheme. In this case, priority is given to handover requests by assigning guard channels (GC) entirely for handover calls among the C channels in a cell. The rest of the M (= C – GC) channels are shared by both new calls and handover calls without priority. A new call is blocked if the progressive call is in state M or is more than that. A handover call is blocked if no channel is accessible in the target cell, which means that the operating state is at state C. The state i (i = 0, 1, . . . , C) of a cell is defined as the number of calls in progress. Let, P(i) be the steady-state probability when the system is in state i. The probabilities, P(i), can be established by analyzing the typical birth–death processes of one-dimensional Markov chain [13].
The relevant state transition rate diagram is shown in Fig. 1. This figure clarifies the birth rate of new and handover calls, as well as their death rate by mean channel holding time (1/μ). From this figure, the state balance equations can be equated as:
In (4), λn and λh denote the call arrival rates of new calls and handover calls, respectively. The steady-state probability, P(i), is found as:
where:
The blocking probability, PB, for a new call is given by:
By this method, the blocking probability of the handover request or call dropping probability, PD, is given by:
The accepting and rejecting call strategy of the FGB scheme is presented in Algorithm 1. Here, the accepting strategies of new calls and handover calls are classified into two different conditions. Channels from M to C are the guard bands that only accept the handover calls.
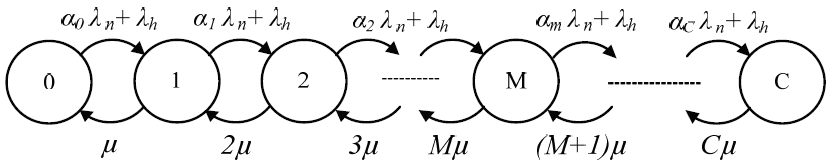
In the FGC scheme, new calls are accepted with a certain probability that depends on the current channel occupancy, which is also recognized as thinning scheme-I [8]. In this case, it is necessary to randomize a parameter, which denotes the probability of the acceptance of a new call. It should be remembered that both schemes accept handover calls as long as channels are available. The Markov process of the FGC scheme is illustrated in Fig. 2. The steady-state probability, P(j), is found as:
where:
The blocking probability, PB, for a new call is given by:
In this case, the call dropping probability, PD, is given by:
Here, α denotes the acceptance factor and i denotes the current state. So, αi denotes the acceptance factor of the current state. In this scheme,α0 = 1, αC = 0 and the others vary randomly between 0 and 1.
The accepting and rejecting policy of the FGC scheme for an arrived call is analyzed in Algorithm 2. In this algorithm a function named rand (0,1) is initiated. It can randomly produce any rational number between 0 and 1 on the basis of occupied channels that accept calls at that ratio and reject the rest of the calls.
The accepting and blocking call strategies of the FGC scheme
Fig. 3 shows the state transition rate diagram of a system with C channels for the LFC scheme. As the name suggests, the LFC scheme is a simplification of the more general FGC scheme, which was described earlier. In the LFC scheme, when the system is in state M, new calls are accepted with the probability α. From states M+1 to C, only handover calls are accepted and from states 0 to M-1, both types of calls are accepted. Thus, the randomization in the LFC scheme is restricted to just one state as compared to the FGC scheme, where randomization could potentially occur at every state.
The handover CDP and new CBP for the LFC scheme can be easily calculated using (8)–(11) by setting αm+1=α, and the values of α i=1, 0 ≤ i ≤ M, and α i=0, M+1< i ≤ C.
The accepting and rejecting call strategy of the FGC scheme is presented in Algorithm 3. This algorithm is quite similar to the FGC scheme, but in the LFC scheme the acceptance factor is previously assigned. From 0 to M this value is 1 and from M+1 to C this value is 0. Only the acceptance factor for state M to M+1 is applicable with some defined values.
The accepting and blocking call strategies of the LFC scheme
The UFC scheme uses new call admission probability, α, which is independent of channel occupancy, to accept new calls. The state transition rate diagram is shown in Fig. 4. This policy accepts handover calls as long as channels are available. This policy can be obtained from the FGB scheme by setting αk=α, (for k = 0, 1, 2, …., C–1). The UFC scheme reserves a non-integral number of guard channels for handover calls by rejecting new calls with some probability. According to the studies given in [9,14,15] show that the UFC scheme has a lower blocking probability for new calls in a low handover and new calls traffic ratio.
The steady-state probability, P(i), is found as:
Here, P(0) can be calculated by the equation and is given as:
The accepting and rejecting strategy of the UFC scheme for an arrived call is presented in Algorithm 4. In this algorithm a function named rand (0, 1) is also initiated, which randomly produces a uniform acceptance factor regardless the channel occupancy. By this technique, it is different from the FGC scheme.
The call accepting strategy of the UFC scheme
The proposed scheme is decorated by hybridizing three sets of bands. A uniform fractional band is assigned between the non-priority and priority bands of the FGB scheme. Therefore, this scheme is known as UFB scheme. The given one-dimensional Markov process in Fig. 5 can illustrate the UFB scheme. The three bands that exist in this scheme accept a call with a uniform acceptance factor by three different patterns. The first band is a non-priority band, where both the new calls and handover calls are accepted with the same priority. In this non-priority band, the acceptance factors for new calls and handover calls are both 1. The second band in the UFB scheme is the fractional band. In this set of channels, the new calls are accepted by a predefined acceptance factor, which is less than 1, and this acceptance factor throughout the band is uniform. In a fractional band, the handover calls are accepted by the acceptance factor of 1. The last band is the integral priority band, where the channels are reserved only for handover calls. In this case, it can be said that the new calls are accepted by this band with zero acceptance factors.
States from 0 to M in Fig. 5, new calls, and handover calls have no priority to access. When the states up to M are occupied, the new calls are accepted by the states from M+1 to N, with a uniform acceptance factor of α. This acceptance factor is independent of the channel occupancy through the band. This type of priority is known as a fractional priority. The states from N+1 to C are reserved only for handover calls like the FGB scheme. This means that these states or the corresponding set of channels accept only handover calls. Hence, the acceptance factors throughout the band for new calls are void. The priority of handover calls given by this band is called integral priority.
The ideas of accepting and blocking the new calls and handover calls by using the UFB scheme are presented in Fig. 6. At first, the network identifies whether the call is a new call or a handover call. If the call is a handover call and there is a free channel in the system, the handover call is accepted by this scheme. If there is no available channel to access, the handover call is blocked. From states 0 to M, all new calls are accepted, but from states M to N, new calls are accepted by a predefined acceptance ratio. For the integral priority band from states N to C the channels are reserved only for handover calls, which means these channels block all new calls.
The process to provide priority to the handover calls is a simple one that is done in two steps. The steady state probability, P(i) is calculated by:
P(0) can usually be calculated by (13). Moreover, the new CBP and handover CDP are given by (17) and (18), respectively:
In Algorithm 5, the accepting and rejecting call strategy of the UFB scheme is given. In this algorithm the function named rand () produces any rational number between 0 and 1 on the basis of the predefined rate and this acceptance factor is only initiated for a band of channels. This acceptance factor works for channels M to N.
The accepting call strategy of the UFB scheme
In this section, we present the simulation results for comparison purposes. These results show how much deviation might occur by using our proposed scheme and the other traditional CAC schemes. We also describe the various features of our proposed scheme.
First of all, we investigated all of the CAC schemes considering the total channels, C=100, the guard band for the FGB scheme and for the LFC scheme, M=90, and in our proposed scheme, N=94. The new call arrival rate is considered from 0 to 6 calls per second in every case. Since in [6–11] the handover call rate is considered to be a fixed ratio of the new call arrival rate, comparing their results with our proposed scheme, the handover call rate is considered to be 1/6 of the new call arrival rate in every simulation. The mean call holding time, 1/μ, is considered for both new calls and handover calls as 90 seconds. To compute the call handover probability mean dwell time, 1/η=360 second.
In the beginning, we examined the new CBP and handover CDP of the various conventional CAC schemes, as well as our proposed scheme, which are compared on a graph in Fig. 7. In this figure we notice that our proposed scheme shows the lowest new CBP than the others and the highest new occurs for the FGC scheme. The proposed UFB scheme shows two different new CPB profiles for two different acceptance factors. Therefore, this acceptance factor is a key factor to control the CPB of this scheme for maintaining the QoS. In the UFC scheme, new calls are accepted by every free channel with a predefined acceptance factor, which causes the new CBP of this scheme to remain steady from a much lower to a higher new call arrival rate. However, this characteristic is not responsible for higher QoS. Since in this case the new call and handover call ratio is not very small, the QoS of the UFC scheme becomes very inadequate. In Fig. 8, we represent the handover CDP comparisons between the conventional schemes and the proposed UFB scheme, where, it is proven that the handover CDP of the UFB scheme have been slightly more increased than the LFC and FGB schemes, but much less than the UFC and FGC schemes. It is also significant that the values of the call acceptance factor do not notably impact the handover CDP of the UFB scheme. According to the outcomes revealed by this figure, it is unblemished that the UFC scheme is the worst CAC scheme in terms of QoS.
The fact-channel utilization in the CAC scheme is a very concerning issue for service providers. Fig. 9 shows channel utilization by the different CAC schemes. The FGC scheme executes the lowest channel utilization profile where the LFC scheme has slightly more utilization achievement than the FGB scheme. Comparatively, beyond the UFB scheme, the LFC scheme shows better performance in the channel utilization aspect. In this figure, it is clear that the proposed UFB scheme utilizes more channels than the FGB, LFC, and FGC schemes and this performance maintains its consistency during lower and higher traffic.
With the augmentation of the overall CBP, the system cost is increased. To reduce the system cost, overall CBP is a concerning issue. Principally, overall CBP depends both on new and handover calls, along with their blocking probabilities. Since the new CBP of the proposed UFB scheme is lower than the other schemes as well as its CDP handover calls being slightly increased, the overall CBP of the UFB scheme can achieve the lowest overall CBP. This comparison is shown in Fig. 10. Here, it is also observed that the UFC and FGC schemes attain very high overall CBP.
Most studies [6–11] consider the handover call rate as a linear function of the new call arrival rate or a constant rate. According to the proposition in [12,13], the handover call arriving rate follows (2) because the handover call rate depends not only on the traffic rate, but also on the handover CDP and new CBP. Therefore, with the increment of new CBP, the handover call rate becomes almost constant. The numerical analyses of the various proposed CAC schemes are to analyze considering the given (2). For this reason, the handover call rate estimation of the different CAC schemes are demonstrated in Fig. 11. Here, it is observed that the handover call rates are not identical for the different schemes.
From Fig. 11, it is observed that the handover call rate of the UFB, LFC, and FGB schemes become almost constant after the new call arrival rate increases at 1.5 calls/s. In this figure, it is also discernible that the handover call rate of the UFB scheme is slightly less than the FGB and LFC schemes. This relationship indicates that considering the handover call rate as a constant function of a new call arrival rate may underestimate or overestimate the new CBP and handover CDP of any CAC scheme.
Without a correct estimation of the call handover rate, it is quite challenging to determine the QoS provisioning measurements. Therefore, we reconnoitered the effect of the fixed and statistical handover call rate on the handover CDP of different CAC schemes and our proposed scheme. To avoid the complexity for graphical presentation, the worst CAC scheme, UFC, is avoided. The LFC scheme is also avoided because this scheme performs the same handover CDP as the FGB scheme. Consequently, we prepared a comparison amongst the FGB, FGC, and UFB schemes on the basis of their handover CDP profiles, as shown in Fig. 12. From this figure, we notice that there is a big difference between the statistical and fixed handover call rate assumption in handover CDP when the traffic rises to a higher value. By the statistical rate, the handover CDP of the FGB and UFB schemes is the same for lower to higher traffic. This is the evidence for the UFB scheme, which does not hold proper QoS.
The new CBP of the proposed scheme depends on the acceptance factors. The acceptance factor and the new CBP maintain a reverse relationship, which is shown in Tables 1 and 2. We observed that as the acceptance factor increases the new CBP decreases. Here, a problem arises with the handover CDP, because as the acceptance probability of the fractional channels of the UFB scheme are set to a higher value, the handover CDP may increase, which is a threat for QoS. For that reason we calculated the handover CDP average increment per fraction with the average decrement of a new CPB per fraction in Tables 1 and 2.
In this paper, we discuss the different features of several conventional CAC schemes and represent their performance numerically. We also proposed a CAC scheme—a UFB scheme. We showed some comparisons of conventional CAC schemes with the UFB scheme in terms of new call blocking probability, handover call dropping probability, channel utilization, and overall call blocking probability. The results show that the aforementioned performances of the proposed scheme are better than the UFC, FGC, and LFC schemes. The proposed scheme maintains the handover CDP at a satisfactory level even in heavy traffic, which ensures the QoS of the network. The proposed scheme also ensures the lowest overall CBP, which reduces the system cost. It is clear that the proposed scheme is an efficient CAC scheme compared to the existing CAC schemes in regards to new CBP, handover CDP, channel utilization, and overall call blocking probability. All of which demonstrate that the scheme optimizes the greatest number of QoS parameters. In addition, this scheme can show lower performance in the context of QoS if anyone chooses more than 5% fractional channels. Therefore, considering these factors, the proposed UFB scheme can be effectively used in very high traffic-oriented wireless networks.
In our future work, we will implement this idea on a multidimensional Markov process for the QoS provisioning of class-based wireless networks.
Acknowledgement
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (No. NRF-2013R1A1A2057922).
Biography
Md. Asadur Rahman
He received B.Sc. and M.Sc. degrees from the department of Electrical and Electronic Engineering of Khulna University of Engineering & Technology (KUET), Bangladesh, in 2012 and 2014, respectively. Since January 2015, under post graduate scholarship of Higher Education Quality Enhancement Project (HEQEP, Sub-Project#3472) of University Grand Commission (UGC) of Bangladesh, he is engaged in the department of Biomedical Engineering of same university as a PhD candidate. Currently his research work is Neuro-Imaging by Functional Near-Infrared Spectroscopy (fNIRS) and Neuro-Image processing. Beyond this research interest, he is also copiously interested in research on advance communication engineering, brain computer interface, and embedded systems.

Biography
Mostafa Zaman Chowdhury
He received his B.Sc. degree in electrical and electronic engineering from Khulna University of Engineering and Technology (KUET), Bangladesh, in 2002. He received his M.Sc. and Ph.D. degrees both in electronics engineering from Kookmin University, Korea, in 2008 and 2012, respectively. In 2003, he joined the Electrical and Electronic Engineering Department at KUET as a faculty member. Currently he is working as an Associate Professor at the same department. In 2008, he received the Excellent Student Award from Kookmin University, South Korea. He has been serving as a reviewer for several SCI/SCIE indexed journals (including IEEE Communications Magazine, IEEE Transaction on Vehicular Technology, IEEE Transactions on Network and Service Management, IEEE Communications Letters, IEEE Journal on Selected Areas in Communications, Wireless Personal Communications (Springer), Wireless Networks (Springer), Mobile Networks and Applications (Springer), International Journal of Communication Systems (Wiley), International Journal of Electronics and Communications (Elsevier), Computer Communications (Elsevier), Recent Patents on Computer Science, KSII Transactions on Internet and Information Systems, and etc.) and IEEE conferences. He has been acting as a TPC member for several international conferences. He has been involved in several Korean and Bangladesh government projects. His research interests include 5G mobile communications, convergence networks, QoS provisioning, mobility management, femtocell networks, optical wireless communications, internet of things (IoT), millimeter wave communication, and VLC networks.

Biography
Yeong Min Jang
He received the B.E. and M.E. degrees both in electronics engineering from Kyungpook National University, Korea, in 1985 and 1987, respectively. He received the doctoral degree in computer science from the University of Massachusetts, USA, in 1999. He worked for ETRI (Electronics and Telecommunications Research Institute) between 1987 and 2000. Since September 2002, he is with the School of Electrical Engineering, Kookmin University, Seoul, Korea. He had been the director of the Ubiquitous IT Convergence Center at Kookmin University since 2005 and the director of LED Convergence Research Center at Kookmin University since 2010. He has organized several conferences and workshops such as International Conference on Ubiquitous and Future Networks (ICUFN) (2009–2015), International Conference on ICT Convergence (ICTC) (2010–2015), International Conference on Information Networking 2015 (ICOIN2015), and International Workshop on Optical Wireless LED Communication Networks (2013–2015). He is currently a member of the IEEE and a life member of KICS (Korean Institute of Communications and Information Sciences). He received the Young Science Award from the Korean Government (2003–2006). He had served as the founding chair of KICS Technical Committee on Communication Networks in 2007 and 2008. He had served as the executive director of KICS between 2006 and 2014. Currently he is the vice president of KICS. He serves as the Co-Editor-in-Chief for ICT Express which is published by Elsevier. He had been the steering chair of Multi Screen Service Forum since 2011 and the steering chair of Society Safety System Forum since 2015. He had served as the chairman of IEEE 802.15 Optical Camera Communications Study Group in 2014. Currently, he is serving as the Chairman of IEEE 802.15.7r1 Optical Wireless Communications Task Group. His research interests include 5G mobile communications, multi-screen convergence, public safety, optical wireless communications, optical camera communication (OCC), and internet of things (IoT).

References
1. A. Sgora, and DD. Vergados, "Handoff prioritization and decision schemes in wireless cellular networks: a survey," IEEE Communications Surveys and Tutorials, vol. 11, no. 4, pp. 57-77, 2009.

2. MZ. Chowdhury, YM. Jang, and ZJ. Haas, "Call admission control based on adaptive bandwidth allocation for wireless networks," Journal of Communications and Networks, vol. 15, no. 1, pp. 15-24, 2013.

3. MZ. Chowdhury, and YM. Jang, "Class-based service connectivity using multi-level bandwidth adaptation in multimedia wireless networks," Wireless Personal Communication, vol. 77, no. 4, pp. 2735-2745, 2014.

4. A. Leelavathi, and GV. Sridhar, "Adaptive bandwidth allocation in wireless networks with multiple degradable quality of service," IOSR Journal of Electronics and Communication Engineering, vol. 2, no. 4, pp. 25-29, 2012.

5. MZ. Chowdhury, MS. Uddin, and YM. Jang, "Dynamic channel allocation for class-based QoS provisioning and call admission in visible light communication," Arabian Journal for Science and Engineering, vol. 39, no. 2, pp. 1007-1016, 2014.

6. R. Ramajee, D. Towsley, and R. Nagarajan, "On optimal call admission control in cellular networks," Wireless Networks, vol. 3, no. 1, pp. 29-41, 1997.

7. Y. Fang, "Thinning schemes for call admission control in wireless networks," IEEE Transactions on Computers, vol. 52, no. 5, pp. 685-687, 2003.

8. Y. Fang, and Y. Zhang, "Call admission control schemes and performance analysis in wireless mobile networks," IEEE Transactions on Vehicular Technology, vol. 51, no. 2, pp. 371-382, 2002.

9. H. Beigy, and MR. Meybodi, "A new fractional channel policy," Journal of High Speed Networks, vol. 13, no. 1, pp. 25-36, 2004.
10. H. Beigy, and MR. Meybodi, "A general call admission policy for next generation wireless networks," Computer Communications, vol. 28, no. 16, pp. 1798-1813, 2005.

11. H. Beigy, and MR. Meybodi, "Adaptive uniform fractional channel algorithms," Iranian Journal of Electrical and Computer Engineering, vol. 3, no. 1, pp. 47-53, 2004.
12. D. Hong, and SS. Rappaport, "Traffic model and performance analysis for cellular mobile radio telephone systems with prioritized and nonprioritized handoff procedures," IEEE Transactions on Vehicular Technology, vol. 35, no. 3, pp. 77-92, 1986.

13. M. Schwartz, in Mobile Wireless Communications, Cambridge: Cambridge University Press, 2005.
Fig. 7
Comparison of new call blocking probabilities among the conventional guard band call admission control (CAC) schemes in addition with the proposed UFB scheme. LFC=limited fractional channel, FGC=fractional guard channel, UFB=uniform fractional band, FGB=fixed guard band, UFC=uniform fractional channel.

Fig. 8
Comparison of handover call dropping probabilities among the conventional guard band call admission control (CAC) schemes in addition with the proposed UFB scheme (handover calls=1/6 times of new calls). LFC=limited fractional channel, FGC=fractional guard channel, UFB=uniform fractional band, FGB=fixed guard band, UFC=uniform fractional channel.

Fig. 9
Assessments of channel utilization among the various call admission control (CAC) schemes. FGB=fixed guard band, UFB=uniform fractional band, LFC=limited fractional channel, UFC=uniform fractional channel.

Fig. 10
Overall call blocking probability estimation of the different call admission control (CAC) schemes. FGB=fixed guard band, FGC=fractional guard channel, UFB=uniform fractional band, LFC=limited fractional channel, UFC=uniform fractional channel.

Fig. 11
Handover call arrival rates estimation of different call admission control (CAC) schemes by statistical analysis. FGB=fixed guard band, LFC=limited fractional channel, UFB=uniform fractional band.
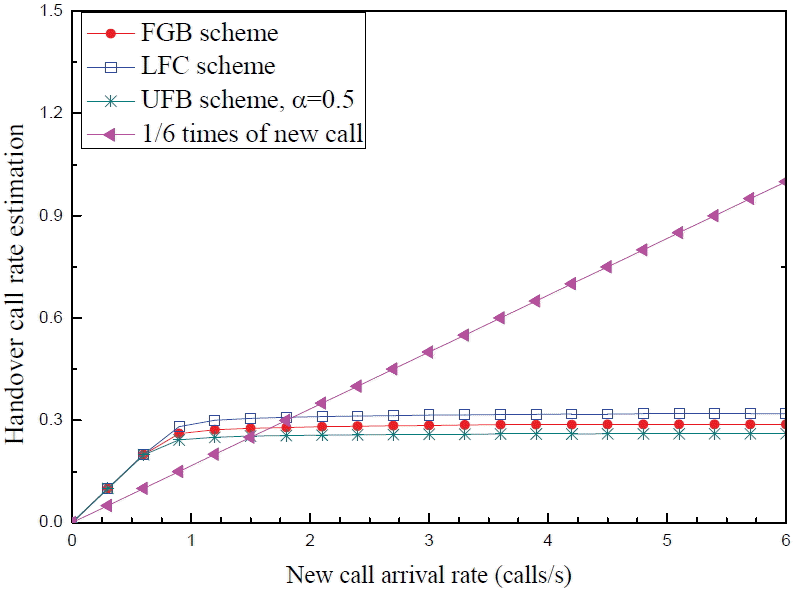
Fig. 12
Comparison of dropping probabilities between the proposed estimation and fixed handover call rate. FGC=fractional guard channel, FGB=fixed guard band, UFB=uniform fractional band.
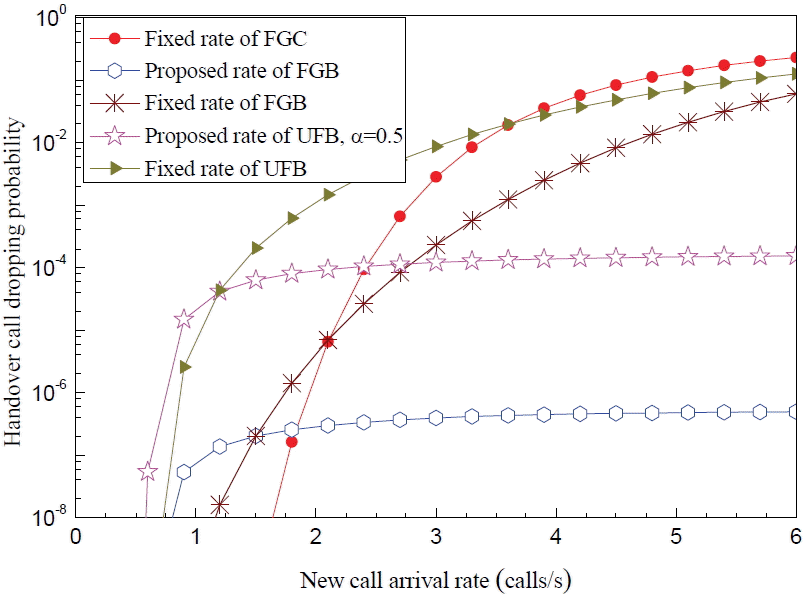
Table 1
New call blocking probability analysis of UFB scheme
Table 2
Handover call dropping probability analysis of UFB scheme