Preethi and Chandrasekar: Seamless Mobility of Heterogeneous Networks Based on Markov Decision Process
Abstract
A mobile terminal will expect a number of handoffs within its call duration. In the event of a mobile call, when a mobile node moves from one cell to another, it should connect to another access point within its range. In case there is a lack of support of its own network, it must changeover to another base station. In the event of moving on to another network, quality of service parameters need to be considered. In our study we have used the Markov decision process approach for a seamless handoff as it gives the optimum results for selecting a network when compared to other multiple attribute decision making processes. We have used the network cost function for selecting the network for handoff and the connection reward function, which is based on the values of the quality of service parameters. We have also examined the constant bit rate and transmission control protocol packet delivery ratio. We used the policy iteration algorithm for determining the optimal policy. Our enhanced handoff algorithm outperforms other previous multiple attribute decision making methods.
Key words: Action, Heterogeneous Handoff, MDP, Policy Iteration, State
1. Introduction
Up until now we endured the analog transmission of signals, which solely depended on wires. When one end is engaged another keeps serene There was no simultaneous conversation. We used a twisted pair of coaxial cables for transmitting analog data, which was time consuming. Later in the digital era the support of the simultaneous wireless transmission of data, and improved the swiftness of communication. In addition to voice data, the deployment of different types of data transmission, such as video, multimedia messages, and animated data, have become more common. In which the multiple sorts of communication is termed as packet data transmission. For supporting such transmissions we have different types of networks, which also depend on larger coverage to smaller coverage. Heterogeneous wireless networks are classified into the following different types: wireless local area networks, such as WiFi; wireless metropolitan area networks, such as WiMAX; wireless personal area networks, such as Bluetooth; and wireless wide area networks, such as the Global System for Mobile Communication (GSM). All of these networks support various types of data transmission rates, received signal strength, and frequency.
Mobility plays a vital role in this current era. Mobile users should be able to utilize different service providers for their needs. When a mobile user moves from one extent to another, there will be signal variation in the mobile device. There must be high bandwidth support for multimedia file transmission, video calls, etc. When the signal level drops down to the threshold value, the mobile device sends the handoff request to the networks that are in proximity. The intra handoff is tranquil. The issue starts when we move into the Inter Handoff. All of the quality of service (QoS) parameters should be checked. Only if it satisfies the quality metrics will the handoff be successful. Handoff in heterogeneous networks can be defined in 4 phases, which is known as a vertical handoff [ 1]. The four phases are known as the handoff initiation, system discovery, handoff decision and handoff execution. The handoff initiation phase triggers the handoff of a mobile terminal (MT). In the system discovery phase, the MT has to decide which networks can be used. In the handoff decision phase, the mobile device has to determine which network it should connect to and continue the call. Our work comprises this phase. For the handoff decision phase, the QoS parameters should be considered. Based on these metrics, the mobile device will select a network for handoff. Some of parameters are bandwidth, signal strength, delay, jitter, packet delivery ratio, etc. Many different algorithms have been proposed for the seamless handover processes. The final phase is the handoff execution phase. Here the mobile terminal connection will be rerouted to the new connection. This phase also comprises the authentication and authorization of the network connection. Handoff can also be classified into a hard handoff and soft handoff. In a hard handoff, the source network connection will be broken and then the new connection will be established. But in a soft handoff, the old connection will continue for some period of time even after the new connection secures its form. The remainder of the paper is organized as follows: Section 2 describes the related work of the paper concerned. Section 3 describes the Markov decision policy. Section 4 discusses about how the Markov decision process (MDP) can be used for a seamless handoff. Section 5 provides details about the implementation of the handoff policy iteration method. In Section 6 we discuss about the output and results of the implementation of MDP for handoff decision making and Section 7 concludes this paper.
2. Related Work
A network selection strategy based on decision-making methods was implemented in [ 1], in which the authors demonstrated a handoff decision based on Multiple Attribute Decision Making (MADM) methods, such as the analytical hierarchy process (AHP) and the ordered weighted averaging process. AHP method was used for ranking and OWA for the weighing of networks. In [ 2] the authors presented a vertical handoff algorithm based on a constrained MDP. They used bandwidth and delay for making the handoff decision. Value iteration and Q-learning algorithms has been used to determine the optimal policy. In [ 3] the authors formulated a vertical handover decision based on the MDP. Bandwidth and delay are taken as the criteria and the value iteration algorithm was used for evaluating the policy. A handoff approach which discussed about the protocol architecture in [ 4] and also different types of metrics used for handoff analyzation. Furthermore, the approach was based on fuzzy relations for handoff evaluation. In [ 5] the authors formulated a handoff decision in a different manner, which is based on a coalition game for reducing the congestion between source and destination mobile nodes. A fuzzy logic based vertical handoff decision that aims at avoiding an unnecessary handoff is proposed in [ 6]. Also the authors used a back propagation neural network algorithm for predicting the received signal strength. The handoff problem presented as a semi MDP in [ 7] by using link cost and signaling cost function. In [ 8] the fuzzy MADM is used for handoff decision making and for determining the handoff, such as price, bandwidth, signal-to-noise ratio (SNR), Sojourn time, seamlessness, and battery consumption. The MDP policy in [ 3] determines the condition under which the handoff is being invoked. In our paper we have presented the ratio of the packet drops, which plays a vital role in a handoff. The constrained MDP policy [ 2] takes the criterions of areas, such as user preference and monetary budget, as the significant terms for handoff decision-making. The data rate is the main key point for all of the networks. The data transfer rate and the throughput is analyzed in this paper and its simulation results are provided. In [ 1] the authors combine two MADM methods to achieve a better outcome. Authors approached in different manners in [ 4– 8] which decides the service providers for handoff, which also discusses about different issues like congestion, call waiting time, etc. In [ 9] the authors classified the vertical handoff and also compared several MADM methods, such as SAW, TOPSIS, GRA, and MEW, and a couple of heuristic policies with the MDP. Optimization problem discussed using value iteration algorithm. The authors in [ 10] formulated the handover decision of the WLAN and line of sight dependent 60 GHz radio systems as an MDP process. In [ 11] the authors examine the handover decision made by MDP in uncertain situations and they also used the application of indoor high quality multi-media. In [ 12], the authors focused on handover based on wireless relay transmission systems. They used profit and cost functions for measuring the quality of service and signaling costs. The authors used the MDP with the value iteration algorithm for handoff decision-making. In [ 13], the authors organized the handover decision as an MDP process by considering the arrival of data, handover delay, and signaling costs. In our work, the MDP predicts the state of a network when its signal level is decreased. We used the network cost function as the criteria and connection reward functions assists to select the optimal network for handoff. We also analyzed the throughput of the networks and the jitter. The evaluation of the CBR and TCP traffic rates is discoursed in Results and Output section. In previous handoff literature, the authors focused on only one handoff operation, but in a normal setting a network can undergo a number of handoffs. Our work is based on two handoff states. The MDP is a chain process that precisely reflects a call initiation and records the signal variations as different states. As such, it is very beneficial in predicting the handoff decision based on the network cost and connection reward functions. The main aim of the paper is to reduce the amount of handoff failures.
3. Markov Decision Process
The MDP model consists of five elements, such as the decision epochs, states, actions, transitions, and rewards [ 14]. The notations in the following equations are from Jay Taylor [ 14]. It consists of the stochastic process along with the decision-making process, which is based on the network cost function and other select actions, such as the handoff decision. The five objectives of MDP processes are as shown below.
T ⊂ {0, ∞} is the set of decision epochs, which are the points in time that the decision is made if the signal reaches the minimum point, and then the action taken as a handoff. We mainly considered processes with countably many decision epochs, in which case T is said to be discrete and we usually take T = {1,2,…., N} or T = {1,2….} depending on whether T is finite or countably infinite. Time is divided into time periods or stages in discrete problems and we assume that each decision epoch occurs at the beginning of a time period. Here T is taken as the call duration. MDP is said to have either a finite horizon or infinite horizon, respectively, depending on whether the call duration is the least upper bound of T (i.e., the supremum is finite or infinite). The duration of a call is infinite since we are unaware of the exact time consumption. Mostly the call duration is finite, because the duration of a call depends on the battery power of a mobile terminal, and also cost. If T = {1….N} is finite, then we will stipulate that no decision is taken on the final decision epoch N. S is the set of states that can be assumed by the process and is called the state space. In this context, S is called the handoff state. Especially, based on the level of the signal it can be decided whether to continue in the same state or to changeover to the handoff state. S can be any measurable set, but for the purpose of our research we will be mainly focused and concerned with the processes that take values in state spaces that are either countable or that are a compact subset of Rn. For each state, s ∈ S, As is the set of actions that are possible when the state of the system is S. The actions will be determined depending on the state. In this case, state is the value of the received signal strength. If it is below the threshold value, a handoff action will be taken. Otherwise, the call will continue with the current network. We write A = ∪s∈SAs for the set of all possible actions and we usually assume that each As is either a countable set or a compact set of Rn. Actions can be chosen either deterministically or randomly. To describe the second possibility, we will write P(As) for the set of probability distributions on As, in which case a randomly chosen action can be specified by a probability distribution Q(●) ∈ P(As). For example, if As is discrete, then the action a ∈ As will be chosen with the probability q(a). If T is discrete, then we must specify how the state of the system changes from one decision epoch to the next. Since we are interested in Markov Decision Processes, these changes are chosen at random from a probability distribution pt(●| s,a) on S. This may depend on the time t, the current state of the system s (the current state depends on the signal strength), and the action a, which would be the handoff-action chosen by the observer.
As a result of choosing the handoff-action a when the system is in low signal state s by the time t, the observer receives a connection-reward rt(s,a), which can be regarded as a profit when positive and as a cost when negative. We assume that the rewards can be calculated, at least in principle, by the observer prior to selecting a particular action. We will also consider problems in which the reward obtained at time t can be expressed as the expected value of a function rt(st,a,st+1), which depends on the state of a system at that time and at the next time. For example:
A decision rule dt will be used to choose the action to be taken at the decision epoch t ∈T. Here, the decision rule is based on the threshold value. If the signal reaches the threshold (i.e., the point of tolerance) the decision rule will be applied to select an action. A decision rule is said to be Markovian if it depends only on the current state of the system (i.e., dt, which is a function of st). Otherwise, the decision rule is said to be history dependent, in which case it depends on the entire history of states and actions from the first decision epoch through the present. Such histories will be denoted as ht = (s1,a1,s2,a2,..st−1,at−1,st). Since a mobile terminal depends only on the current state of the signal, we use the Markovian Policy. The decision rule is further classified into deterministic and randomized. A randomized action is based on probability distribution.
The policy π is a sequence of decision rules such as d1,d2,d3,… for every decision epoch. The policy is said to be Markovian if the decision rule specified by the policy has the corresponding properties. Since a MDP is a stochastic process, the successive states and actions realized by that process form a sequence of random variables. The following notations are used for these variables: for each t ∈ T, let Xt be the set of states that belongs to S and Yt is the set of actions taken based on the state S, where Yt ∈ As. The Markov reward process is given by (Xt,rt(Xt,Yt):t ∈ T).
4. Markov Policy Based Seamless Handoff
In this paper, we follow Ω as the policy, based on the decision rule. A set of decision epochs is given as T = {1,2,...} and that the reward functions and transition probabilities do not vary over time. For example, for every t ∈T we have rt(s, a) = r(s, a) and pt(ψ| s, a) = p(ψ| s, a). Here p(ψ | s, a) is the state occupied at time t = 2 (next state). We deal with the stationary policies, in which we denote Ω = d∞ = (d, d,...). This means that the same decision rule is used in every decision epoch. Here the decision rule is to choose the optimal network for handoff. Since Ω is Markovian, there are several performance metrics that can be used to assign a value to the policy, which depends on the initial state of the system. The expected total reward of Ω is given as:
where
vmΩ (s) is the total expected reward in a model restricted to m decision epochs and the terminal reward 0. In general, this limit does not exist or it may exist but is equal to ± ∞. If there is a limit, it need not be the case that the limit and expectation can be interchanged. An alternative performance metric is the expected total discounted reward of Ω, which is defined to be:
where λ ∈ [0,1) is the discount rate. Notice that the limit is guaranteed to exist if the absolute value of the reward function is uniformly bounded. For example, if |r(s,a)| ≤ N for all s ∈ S and a ∈ As, then the total expected discounted reward is also uniformly bounded:
Here we have taken the parameters such as throughput and jitter as the criterions for connection reward functions. Based on these two parameters, rewards will be given. Formula ( 4) can also be written as: which is called the network cost function. Where
EsΩ is the expected total reward derived from the state (s) and policy (Ω) and
r(XtT)(1XtJ)(Yt) is the reward offered for the action (Yt) based on the throughput (
XtT) and jitter (
1XtJ) at the given time.
5. Handoff Policy Evaluation
Suppose policy Ω = (d1, d 2,...) is the Markovian policy. The total expected reward can be expressed as:
In this proposed MDP method, within the call duration at time t = 1..∞, we have two states S = ( s1, s2) in which the WiFi network tries to connect to other networks that are available, such as GSM, WiMAX, and CDMA. Actions are named as A1, A2 and A3 where action A1 refers to a changeover from WiFi to WiMAX, A2 as WiFi to GSM, and A3 as WiFi to CDMA. The rewards are represented as data rate units in Table 1. A1, A2 A3
The discount factor (λ ) has been given as 0.5. We estimated the expected total reward for all the three networks to be:
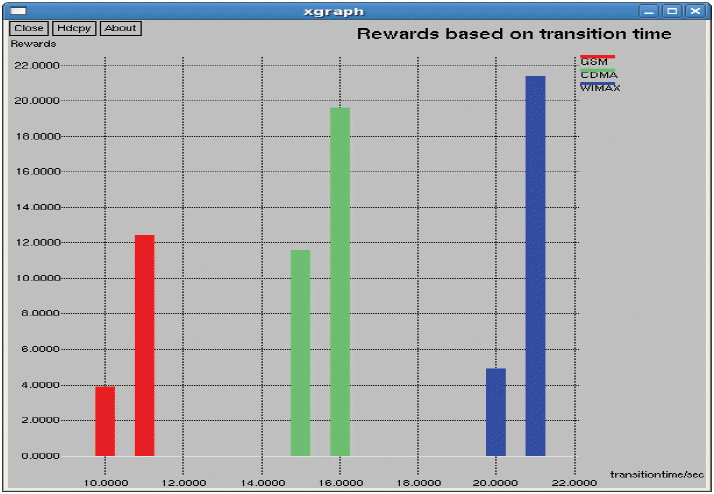
In the 2nd state, R2(1) = 9.7, R2(2) = 8.75, and R2(3) = 15.6, in the 1st state WiMAX gets the highest connection reward for handoff. In State 2, CDMA gets the highest reward. At this juncture, we calculate the expected transition time, LΩ
LΩ(1,3) = 1+ 0.2LΩ(1,3) + 0.2LΩ(2,3), LΩ(2,3) =1+ 0.3LΩ(1,3) + 0.4LΩ(2,3) and LΩ(3,3) =1+ LΩ(1,3) are measured. Finally, by rearranging the first equation we get, LΩ(1,3) = 3.9, LΩ(2,3) = 11.6 and LΩ(3,3) = 4.9. We now estimate the expected rewards obtained from the current state to next state under policy Ω.
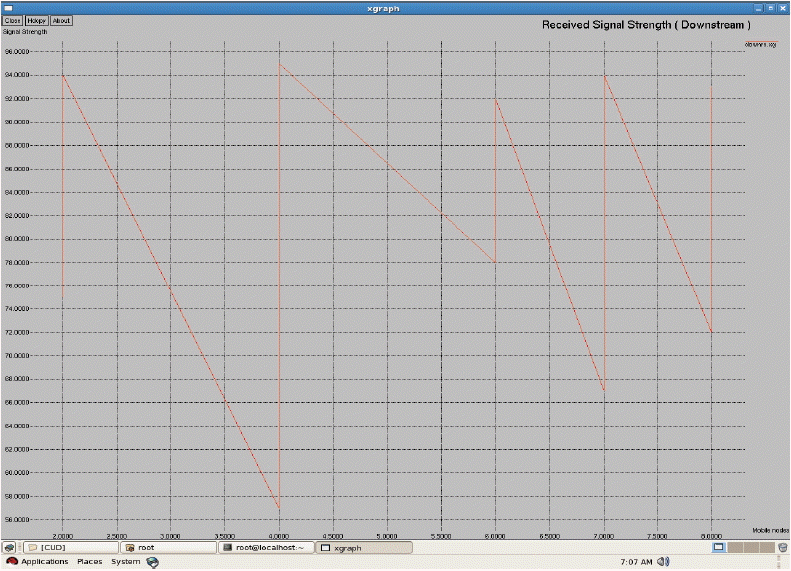
Where ri,k,Ω is the reward of transition from i to k in one step (this is the reward gained in the initial state). Since r1,k,Ω = 6, r2,k,Ω = 5, and r3,k,Ω= 9. From Table 2, we received the rewards, such as RΩ(1,3) = 6 + 0.2 RΩ(1,3) + 0.2 RΩ(2,3), RΩ(2,3) = 5 + 0.3 RΩ(1,3) + 0.4 RΩ(2,3), and RΩ(3,3) = 9 + RΩ(1,3). We assess RΩ(1,3) = 12.4, RΩ(2,3) = 19.6, and RΩ(3,3) = 21.4 by reordering the equations. The average reward obtained under policy Ω is thus: where ψ denotes the next state, in which we calculate the connection rewards for each state transitions. We used the dataset of RSS measurements [ 15] that were collected by the University of Colorado’s Wide-Area Radio Testbed. We used the received signal strength for downstream, as shown in Fig. 1. In Fig. 1, the horizontal co-ordinate represents the mobile nodes and the vertical co-ordinate represents the signal strength. Node 4 has reached a higher level and gradually decreases to a lower level. If the signal strength is more than 90, then it is strong, and if it extends below 60, it is lower. The mobile node sends a warning message that the signal is getting lower than the ‘point of tolerance’ if it stretches down to lower. At this point we use the threshold value as the point of tolerance. Here, the mobile node sends the handoff-request to all the nearby nodes. It gets the information about the networks that are in proximity. By applying the handoff policy iteration algorithm, we receive the rewards. Suppose the rewards match the given criteria, then the handoff is successful, otherwise it will be dropped. Fig. 2 characterizes the handoff sequence.
6. Results and Discussion
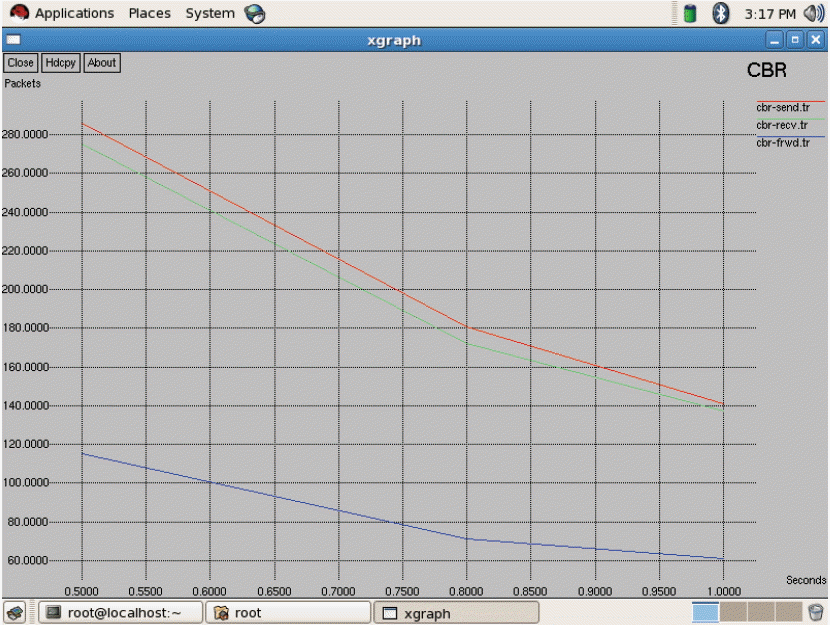
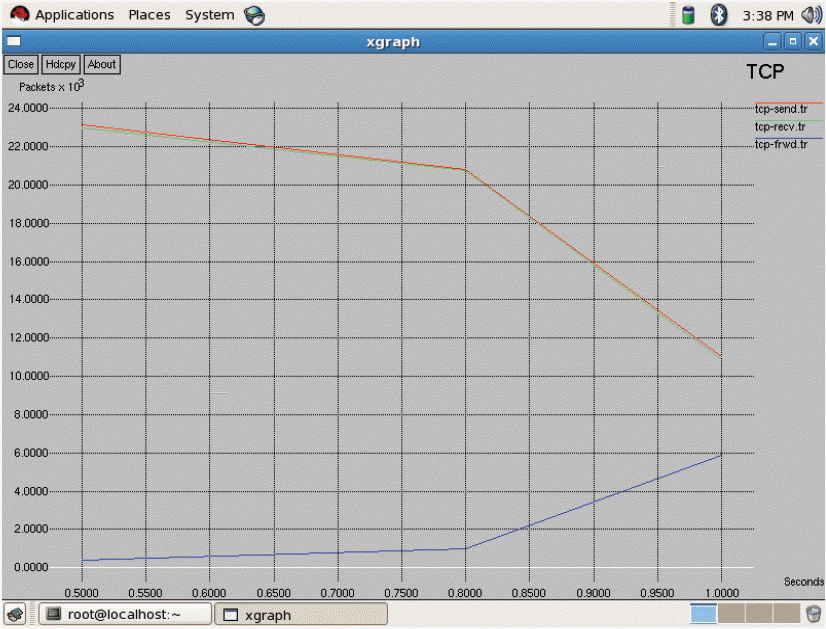
As seen in Fig. 3 above, all three of the networks have 2 bars, which indicate two states. The first bar denotes the first state and second bar denotes second state, respectively. By applying the policy iteration in the first state, WiMAX gets the high score. In the second state, CDMA gets a high score. After finding the expected transition time for each network, we discover that the rewards and transition time for GSM is low, as seen in Fig. 4. The transition time of CDMA is very high and its reward has a very high value. When compared with both of these two networks, WiMAX has a low transition time and a high reward. Consequently, WiMAX gets optimum for being selected for handoff. The average reward has been calculated. This will be useful when there are more states and more actions. For each and every transition the average reward can be obtained and compared to predict the optimal network for handoff decision-making. In the Markov process we have analyzed the entire duration of a call. We only used 2 state transitions and predicted the optimal network. Other MADM methods only use a context aware calculation for finding the desired networks to handover. Throughput measures all of the three networks shown in Fig. 5. From Fig. 5, it is evident that WiMAX has higher throughput compared to GSM and CDMA. In general, the throughput depends on the data transfer rate of the respective service providers. Next to WiMAX, CDMA secures the high position, in which it supports a soft handoff. As seen in Fig. 6, the packet loss of WiMAX is also higher. On the other hand, GSM and CDMA have an equal range for packet loss. In the handoff simulation test bed, two protocols such as AODV and DSDV are examinated. DSDV has more packet loss compared to AODV. The basic data rate is set as 2 MB. Throughput 1 represents GSM, throughput 2 as WiMAX, and throughput 3 for CDMA. The same series of network are represented in Figs. 6 and 7 for jitter and packet losses. From the Fig. 7, jitter measure for all the three networks has been driven. The GSM network has the higher jitter values than WiMAX and CDMA do. Also, the delay is initially very high for GSM and it gradually decreases after 5 seconds. Furthermore, its delay is higher than the other two networks. WiMAX does not have as much of a delay as compared to the other two networks. From all of these outputs we can recommend WiMAX for the network selection of handing off. As shown in Figs. 8 and 9, we have also observed the traffic scenarios of TCP and CBR for the three networks. We analyzed the different pause times such as 0.5, 0.8, and 1.0. The CBR traffic shows the packet delivery rate of 275 out of 286 packets. The ratio shows that 96% of packets were delivered at the pause time 0.5. For the pause time 0.8, 172 out of 181 packets reached their destination, which is a 95% delivery rate. Pause time 1.0 shows the packet transference of 97%, in which 137 packets delivered out of 141 packets. We have analyzed the simulation in two different traffic agents, such as TCP/FTP and CBR/UDP. In TCP, for the pause time of 0.5. By using TCP, the conveyance of packets towards the destination mobile nodes are 23,151 out of 22,994, which demonstrates a 99% delivery rate. For the 0.8 and 1.0 pause times we have 99% and 98% of packet delivery ratios en route for the destination. We set the maximum speed rate as 20 seconds and 2 packets were delivered per second. The simulation timing was about 80 seconds. As compared to CBR, TCP has the added delivery ratio of packets. The packet size was set at the default size, which is 512 MB. In both of the traffic scenarios it is obvious that if we increase the pause time, the packet drops are augmented. In the Figs. 8 and 9, the red line indicates the packets sent, the green line indicates the packets received at the destination, and the blue line indicates the packets forwarded in between the source and destination nodes. Here we have measured the total number of packets delivered for all three networks.
7. Conclusion
As demonstrated from the rewards obtained and the simulation results, WiMAX has the highest score and the shortest transition time, as compared to other networks. On the other hand, CDMA can be chosen for handoff since it gives higher rewards and also it uses soft handoff, which is one of the advantages of this network. While making handoff decisions we have to consider all possible criterions. In this work, we have taken criteria such as data rate, jitter, throughput measures and packet loss. User preferences should be taken into account, which will be addressed in our future work. By using the policy iteration method, we can predict the network to handoff in which it gets vetoed of ping-pong effect and the handoff failure.
Acknowledgement
The first author extends her gratitude to UGC as this research work was supported by the Major Research Project, under grant (No. 41-611/2012(SR), UGC XI Plan).
Biography
G. A. Preethi
She has completed her M.Sc. in Computer science in 2002. M.Phil (Computer Science) in the year 2011. Worked as a Guest Lecturer in the Department of Computer Science in Periyar University, Salem for a year from 2011–2012. She joined as a Project Fellow in the same department under UGC Major Project from the year 2012. Currently she is pursuing her Ph.D. degree under the guidance of Dr. C. Chandrasekar. Her research interests are Mobile Computing, Wireless Technology. She received the best paper award in an International Conference on Advances in Engineering and Technology (ICAET) held in E.G.S. Pillai Engineering college, Nagapattinam, Tamil Nadu, India.
Biography
C. Chandrasekar
He received his Ph.D. degree from Periyar University. He is working as an Associate Professor in the Department of Computer Science, Periyar University, Salem, Tamil Nadu, India. His area of interest include Wireless networking, Mobile Computing, Image Processing, Data Mining, Computer Communications and Networks. He is a research guide at various universities in India. He has published more than 80 technical papers at various National & International conferences and 50 journals. He is a senior member of ISTE and CSI.
Reference
1. GA. Preethi, and C. Chandrasekar, "A network selection algorithm based on AHP-OWA methods," in Proceedings of the 6th Joint IFIP Wireless and Mobile Networking Conference, Dubai, United Arab Emirates, 2013, pp. 1-4.
2. C. Sun, E. Stevens-Navarro, and VW. Wong, "A constrained MDP-based vertical handoff decision algorithm for 4G wireless networks," in Proceedings of the IEEE International Conference on Communications (ICC’08), Beijing, China, 2008, pp. 2169-2174.  3. E. Stevens-Navarro, Y. Lin, and VW. Wong, "An MDP-based vertical handoff decision algorithm for heterogeneous wireless networks," IEEE Transactions on Vehicular Technology, vol. 57, no. 2, pp. 1243-1254, Mar.;2008.  4. RK. Singh, A. Asthana, A. Balyan, SJ. Gupta, and P. Kumar, "Vertical handoffs in fourth generation wireless networks," International Journal of Soft Computing and Engineering (IJSCE), vol. 2, no. 2, pp. 481-490, 2012.
5. SV. Saboji, and CB. Akki, "Congestion-aware proactive vertical handoff decision using coalition game," International Journal of Soft Computing and Engineering (IJSCE), vol. 1, no. 6, pp. 91-97, 2012.
6. S. Kunarak, and R. Suleesathira, "Predictive RSS with fuzzy logic based vertical handoff decision scheme for seamless ubiquitous access," in Mobile Ad Hoc Networks Protocol Design, Croatia: InTech, 2011, pp. 261-280.  7. VW. Wong, ME. Lewis, and VC. Leung, "Stochastic control of path optimization for inter switch handoffs in wireless ATM networks," IEEE/ACM Transactions on Networking, vol. 9, no. 3, pp. 336-250, Jun.;2001.  8. W. Zhang, "Handover decision using fuzzy MADM in heterogeneous networks," in Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC2004), Atlanta, GA, 2004, pp. 653-658.
9. E. Stevens-Navarro, U. Pineda-Rico, and J. Acosta-Elias, "Vertical handover in beyond third generation (B3G) wireless networks," International Journal of Future Generation Communication and Networking, vol. 1, no. 1, pp. 51-58, Dec.;2008.
10. J. Wang, R. Venkatasha Prasad, and IGMM. Niemegeers, "Solving the incertitude of vertical handovers in heterogeneous mobile wireless network using MDP," in Proceedings of the IEEE International Conference on Communications (ICC’08), Beijing, China, 2008, pp. 2187-2192.  11. J. Wang, R. Venkatasha Prasad, and IGMM. Niemegeers, "Solving the uncertainty of vertical handovers in multi-radio home networks," Computer Communications, vol. 33, no. 9, pp. 1122-1132, Jun.;2010.  12. X. Dang, JY. Wang, and Z. Cao, "MDP-based handover policy in wireless relay systems," EURASIP Journal on Wireless Communications and Networking, vol. 2012, pp. 1-13, 2012.  13. J. Pan, and W. Zhang, "An MDP-based handover decision algorithm in hierarchical LTE networks," in Proceedings of the IEEE Vehicular Technology Conference, Quebec, Canada, 2012, pp. 1-5. 
|