Khan, Chai, See, and Khan: X-Ray Image Enhancement Using a Boundary Division Wiener Filter and Wavelet-Based Image Fusion Approach
Abstract
To resolve the problems of Poisson/impulse noise, blurriness, and sharpness in degraded X-ray images, a novel and efficient enhancement algorithm based on X-ray image fusion using a discrete wavelet transform is proposed in this paper. The proposed algorithm consists of two basics. First, it applies the techniques of boundary division to detect Poisson and impulse noise corrupted pixels and then uses the Wiener filter approach to restore those corrupted pixels. Second, it applies the sharpening technique to the same degraded X-ray image. Thus, it has two source X-ray images, which individually preserve the enhancement effects. The details and approximations of these sources X-ray images are fused via different fusion rules in the wavelet domain. The results of the experiment show that the proposed algorithm successfully combines the merits of the Wiener filter and sharpening and achieves a significant proficiency in the enhancement of degraded X-ray images exhibiting Poisson noise, blurriness, and edge details.
Key words: Image Enhancement, Image Fusion, Poisson/Impulse Noise, Sharpening, Wavelet Transform
1. Introduction
Image enhancement is an essential technique in the field of image preprocessing. In previous research, a number of enhancement algorithms have been used in different image processing applications. However, these traditional algorithms are limited to only having the ability to solve a single, specific problem of degraded images. For instance, histogram specification can improve the specific area of interest. Similarly, histogram equalization can enhance an image’s contrast by extending the dynamic range of its grey variation, and sharpening can raise an image’s sharpness through paying contours and emphasizing edges. Traditional approaches cannot provide a satisfactory consequential image to fulfill the enhancement demand of applications.
Hopefully, image fusion can assist in providing a solution to these enhancement issues. The aim of image fusion exists in combining multiple source X-ray images into a fused X-ray image that integrates more useful information than the individual one. For about two decades, image fusion has emerged as an encouraging image processing technique in many fields, like flood plan mapping, remote sensing, and medicine. Out of various image fusion techniques, the kind of fusion based on wavelet transform has been proven to be an important trend in this field of research in recent years because of its outstanding performance [ 1– 4]. In the proposed approach, wavelet-based image fusion is employed to enhance degraded X-ray images by merging the performance of the boundary division Wiener filter approach and sharpening. First, the boundary division Wiener filter and sharpening approaches are separately applied to the same degraded X-ray image in order to obtain de-noised, de-blurred, and sharp X-ray image sources. Then, these two source X-ray images are fused via special rules in the wavelet domain to acquire the enhanced X-ray image. The results of the experiment show that our proposed algorithm impressively improves the degraded X-ray images and synchronously provides acceptable details and noise free X-ray images.
1.1 Fast Wavelet Transform Algorithm
The unique quality of localization, both in the spatial domain and frequency domain, permits the wavelet transform to be extensively recycled in image processing and analyzing fields. The fast wavelet transform algorithm proposed by Mallat [ 6] contributes much to this recognition. For wavelet decomposition, the fast algorithm employs two one-dimension filters to understand two-dimension wavelet transform [ 5, 6]. In Level 2- j, the decomposition transform can be given by the following expression: Where H and G are low-pass and high-pass filters, respectively, and the subscripts, r and c, represent horizontal and vertical filtering, correspondingly. Therefore, Cj is a smooth sub-image that indicates the coarse approximation of Cj-1, and
Djk (k=1,2,3) are detailed sub-images, where each represents the information in the horizontal, vertical, or diagonal direction of the image Cj-1. For wavelet reconstruction, the fast algorithm runs the inverse wavelet transform by another two one-dimension filters of H* and G*, which are conjugate transpose matrixes of H and G, respectively. Their construction algorithm can be defined by the following expression:
2. Image Enhancement Algorithm Using the Boundary Division Wiener Filter and Image Fusion Approach
X-ray images normally degraded with Poisson noise, are de-blurred and have a low contrast. Poisson noise arises when the finite number of photons carrying energy is small enough to give rise to detectable statistical fluctuations in a measurement [ 7]. These particles are called ‘electrons’ in an electronic circuit and ‘photons’ in an optical device. Unlike others digital images, X-ray images are usually degraded by Poisson noise and sometimes by impulse noise. Most of the previous research work is normally on impulse noise removal. It has been concluded that recent research is full with inadequate strategies and while research studies have introduced very efficient techniques for impulse noise elimination, they are not trying to mitigate Poisson noise problems. One useful method is when the median filter, weighted median filter, center weighted median filter, and switching median filter use the boundary discriminative noise detection (BDND), which can de-noise digital images contaminated with impulse noise [ 8– 11]. However, because of a lower penetration rate, the random dropping of photons, and the size of detector matter, X-ray images are degraded with Poisson noise. Therefore, our proposed state-of-the-art boundary division Wiener filter is the ultimate filter for Poisson noise degraded images. On the contrary, although sharpening cannot remarkably improve image contrast, this processing greatly enhances the edge details by employing the differential operation of the Laplace operator [ 12]. Thus, the complementary relationship of the boundary division Wiener filter and sharpening approaches clearly emerges in image enhancement. An approach for removing Poisson noise in X-ray images using a wavelet domain is proposed in [ 13]. However, the basic limitation to this idea is that it filters all pixels with a Wiener filter whether they are corrupted or not. Some research studies have worked on Poisson noise in a different domain [ 14]. These studies have proposed a framework to reduce Poisson noise using wavelet transform and a modified Bayes Shrink method in the wavelet domain. Patidar et al. [ 15] use a median filter, mean filter, Wiener filter for impulse noise, Gaussian noise, speckle noise, and Poisson noise reduction. The proposed boundary division Wiener filter approach utilizes the above complementary quality through image fusion to de-noise, de-blur, and enrich the edges of degraded X-ray images simultaneously. The schematic diagram of the proposed algorithm is shown in Fig. 1, and the processing flow is demonstrated as explained below.
Apply the boundary division approach with the Wiener filter and sharpening, respectively, to obtain two complementary source X-ray images (i.e. de-noised and sharpened X-ray image). Decompose the de-noised X-ray image and sharpened X-ray image with a fast digital wavelet transform (DWT) algorithm. Fuse the approximate and detailed coefficients of the DWT decomposition, respectively, through different rules to get fused coefficients. Reconstruct the image from the fused coefficients through an inverse digital wavelet transform (IDWT).
Fusion rules play a key role in image fusion and researchers have developed some fusion rules for various applications [ 16, 17]. In recent research, different rules are used to, respectively, deal with approximate and detail coefficients. Let ‘ P’ and ‘ Q’ denote the two sources X-ray images—the de-noised X-ray image and sharpened X-ray image. In addition, ‘ F’ denotes the fused result of ‘ P’ and ‘ Q’. For the approximate coefficients, the following rule is applied: where α performs as a weight coefficient that can adjust the portions of “P” and “Q” to control the blurriness of the fused X-ray image. It is empirically determined that scale 4 can provide satisfactory results for the fusion of de-noised and sharpened X-ray images according to different image conditions. In our future work, an adaptive algorithm will be developed to determine the value of α.
The detail coefficients are combined by the following fusion rule:
This processing ensures that the fusion algorithm can efficiently combine the above enhancement effects in detail to make the resulting X-ray image clearer than any of the sources.
The detailed explanation of our state-of-the-art boundary division Wiener filter approach is as laid out below.
Read the noisy X-ray image and imposea 7×7 window around the ith and jth pixels and create a Binary Map (BM) of the same sub-image. Store all the values under the window in a vector (V) and sort it in ascending order. Compute the square of vector V. Find the lowest and highest values in vector V. From the lowest to (Lowest + Highest) / 2, compute the difference of all pixels in V and store it in vector D. Find the maximum difference in D (From Lowest to (Lowest + Highest) / 2) and mark its corresponding pixel in V as b1. Similarly, from (Lowest + Highest) / 2 to Highest, compute the difference of all pixels in V and store it in vector D. Find the maximum difference in D (From Lowest + Highest) / 2 to Highest) and mark its corresponding pixel in V as b2. If the selected pixel belongs to the middle cluster then uncorrupt it. Store the values of middle cluster into vector Dr. Compute wiener of vector Dr and store it in vector Z. -
Replace imposed window values with Z values.
ELSE,
Invoke the 2nd iteration and impose a 3×3 window on the same pixel and return to Step 2. End.
The pseudo-code for our proposed boundary division approach with a Wiener filter is illustrated in Fig. 2. At the end of this paper, Appendix 1 illustrates the flowchart of the boundary division Wiener filter approach.
3. Analysis of the Proposed Algorithm
First and foremost, the important aspect of the proposed algorithm is that it detects Poisson noise corrupted pixels and then restores it with the Wiener filter approach, while according to [ 8– 10, 13], there is no such phenomena for detecting only corrupted pixels. Second, in our proposed algorithm, the 7×7 window is imposed on each pixel in the first stage/iteration. However, according to [ 11], a 21×21 window is imposed in the first stage on each pixel. This means that about 400 extra comparisons will be required to check a pixel value, which is a time consuming job, and the effectiveness of the validation is also noticeably weakened. Moreover, we know that a large window size causes image blurriness. As such, by using a 21×21 window the resulting image will have more blurriness. However, we can state that our proposed boundary division Wiener filter algorithm using a 7×7 window size avoids this many comparisons and a blurry image.
4. Results
The performance of our proposed filter was tested against the ideas presented in [ 11, 18, 19]. Objective comparisons of the performances of these filters on images corrupted by various impulse noises and Poisson noise were made with the mean square error (MSE) and peak signal-to-noise ratio (PSNR) of the images restored by them. Table 1 shows missed detections and false alarms (to avoid using a big space, we have taken intensity values that are only in the range of (151–165 and 161–190), instead of the full image; time taken after applying histogram equalization, wavelet approach, a BDND with a switching median filter and our proposed approach) and Table 2 shows the time taken by all existing and proposed approaches. Next, Table 2 shows the time taken by all of the approaches mentioned above during noisy pixel detection for an X-ray image of baggage (image size 256×256). Next, Figs. 3 and 4 illustrate the MSE and PSNR values of all cited approaches and our proposed approach. The X-ray image of baggage was contaminated with 30% Poisson and impulse noises.
Figs. 5 and 6 show the MSE and PSNR values of all cited approaches and our proposed approach. The X-ray image of baggage was contaminated with a 90% density of Poisson and impulse noises.
The results of these tables reveal that our proposed approach provides the best results.
5. Conclusion
We have proposed a novel enhancement algorithm that is directed at addressing the problems of Poisson noise, blurriness, and sharpness in degraded images. The algorithm utilizes a wavelet-based image fusion to accomplish this multiplex enhancement job. The results of our investigations prove that our proposed enhancement algorithm can efficiently combine the merits of the boundary division Wiener filter and sharpening and that it can de-noise, de-blur, and sharpen the degraded X-ray image all at the same time.
The tremendous advantage of our proposed method is that it is simple and can be realized even faster than all other existing filters and that it can detect corrupted pixels in an efficient and reliable way and enhance the X-ray image. It removes blurriness from an X-ray image while also de-noising it.
Biography
Sajid Ullah Khan
He was born in KPK, Province, Pakistan, in 1982. He received the B.S. degree from Gomal University, D.I.Khan in 2005 and the M.S. degree from the university of Science & Technology, Bannu, Pakistan in 2011, both in Computer Science. He is currently pursuing Ph.D. degree with the Faculty of Computer Science & Information Technology, Malaysia. His research interests include image processing and computer vision. He had worked in different government and public organization for almost 10 years which include both teaching and conducting research. He has published journal papers, book and conference proceedings and attended various talks and seminars.
Biography
Wang Yin Chai
He was born in Malaysia. He received his Bachelor of Science and Computer with Education, Major in Computer and Mathematics from University Technology Malaysia (UTM), and his Ph.D. degree (Geographical Information Systems), from University Sains Malaysia (USM). He is currently working as a professor in University Malaysia Sarawak (UNIMAS), Malaysia. His research interests are GIS, Spatial Technology, Image Processing, and Computer Vision. He has been working in UNIMAS for more than 15 years. Besides that, he is the director of Center of Excellence for Image Analysis and Spatial Technology in UNIMAS. He had secured more than RM1.7 Million of research grants and consultation projects. Moreover, Prof. Wang has been working as an editor and reviewer in different journals and conferences. He has supervised more than 40 PhD and Master Students.
Biography
Chai Soo See
She was born in Malaysia. She received the M.Sc. (IT) degree from University Malaysia Sarawak (UNIMAS), Malaysia and Ph.D. degree from Curtin University of Technology, Australia. She is currently working as a senior lecturer in University Malaysia Sarawak, Malaysia. Her research interests include image processing, GIS, computer vision and spatial technology. She is serving as a senior lecturer in UNIMAS for more than 5 years. Dr. Chai is supervising Ph.D. and Master Students at national and international level.
Biography
Amjad Khan
He was born in Bannu KPK, Pakistan in 1986. He received his B.S. degree in Computer Science in 2009 from University of Science & Technology Bannu, KPK, Pakistan. He completed his M.S. in Computer Science (research field image processing) in 2012 from Comsats Institute of Information Technology WahCantt. Currently, he is a Ph.D. candidate in the Department of Computer Science at the University of Malaysia Sarawak (UNIAMS), Malaysia focusing on biomedical imaging and automatic segmentation on cardiac MRI-LV applications. His research interests include biomedical image analysis, computer vision, machine learning, dynamical systems theory and robotics. He is particularly interested in the development of mathematical methods for the interpretation of high-dimensional data, such as images, videos, and biomedical data.
References
1. Z. Zhang, and RS. Blum, "A categorization of multiscale-decomposition-based image fusion schemes with a performance study for a digital camera application," Proceeding of IEEE, vol. 87, no. 8, pp. 1315-1326, 1999.  2. V. Petrovic, and T. Cootes, "Objectively adaptive image fusion," Information Fusion, vol. 8, no. 2, pp. 168-176, 2007.  3. G. Pajares, and JM. De La Cruz, "A wavelet-based image fusion tutorial," Pattern Recognition, vol. 37, no. 9, pp. 1855-1872, 2004.  4. SU. Khan, YC. Wang, and SS. Chai, "A novel noise removal technique of X-ray carry-on luggage for detection of contraband/illicit object(s)," International Journal of Engineering and Advance Technology, vol. 2, no. 3, pp. 94-99, 2013.
5. SG. Mallat, "A theory for multi-resolution signal decomposition: the wavelet representation," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 11, no. 7, pp. 674-693, 1989.  6. SG. Mallat, in A Wavelet Tour of Signal Processing, San Diego, CA: Academic Press, 1998, pp. 302-310.
7. MA. Farooque, and JS. Rohankar, "Survey on various noises and techniques for denoising the color image," International Journal of Application or Innovation in Engineering & Management (IJAIEM), vol. 2, no. 11, pp. 217-221, 2013.
8. TS. Huang, GJ. Yang, and GY. Tang, "Fast two-dimensional median filtering algorithm," IEEE Transactions on Acoustics, Speech, Signal Process, vol. 27, no. 1, pp. 13-18, 1979.  9. R. Yang, Y. Lin, M. Gabbouj, J. Astola, and Y. Neuvo, "Optimal weighted median filters under structural constraints," IEEE Transactions on Signal Processing, vol. 43, no. 3, pp. 591-604, 1995.  10. T. Sun, M. Gabbouj, and Y. Neuvo, "Center weighted median filters: some properties and applications in image processing," Signal Processing, vol. 35, no. 3, pp. 213-229, 1994.  11. PE. Ng, and KK. Ma, "A switching median filter with boundary discriminative noise detection for extremely corrupted images," IEEE Transactions on Image Processing, vol. 15, no. 6, pp. 1506-1516, 2006.  12. RC. Gonzalez, and RE. Woods, in Digital Image Processing, 2nd ed, Upper Saddle River, NJ: Prentice Hall, 2002, pp. 88-94.
13. L. Wang, J. Lu, Y. Li, T. Yahagi, and T. Okamoto, "Noise reduction using wavelet with application to medical X-ray image," in Proceedings of IEEE International Conference on Industrial Technology (ICIT2005), Hong Kong, 2005, pp. 33-38.  14. M. Sakata, and K. Ogawa, "Noise reduction and contrast enhancement for small-dose X-ray images in wavelet domain," in 2009 IEEE Nuclear Science Symposium Conference Record (NSS/MIC), Orlando, FL, 2009, pp. 2924-2929.  15. P. Patidar, M. Gupta, S. Srivastava, and AK. Nagawat, "Image de-noising by various filters for different noise," International Journal of Computer Applications, vol. 9, no. 4, pp. 45-50, 2010.  16. GQ. Tao, QD. Li, and GH. Lu, "Study on image fusion based on different fusion rules of wavelet transform," Infrared and Laser Engineering (China), vol. 32, no. 2, pp. 173-176, 2003.
17. BJ. Tao, JR. Wang, and JP. Xu, "Study on image fusion based on different fusion rules of wavelet transform," Infrared Technology (China), vol. 28, no. 7, pp. 431-434, 2006.
18. M. Ashima, and A. Tayal, "Impulse noise detection and filtering in switching median filters," International Journal of Computer Applications, vol. 45, no. 13, pp. 40-45, 2012.
19. A. Nasimudeen, MS. Nasir, and R. Tatavarti, "Directional switching median filter using boundary discriminative noise detection by elimination," Signal, Image and Video Processing, vol. 6, no. 4, pp. 613-624, 2012. 
Fig. 1
Block diagram of proposed enhancement algorithm. 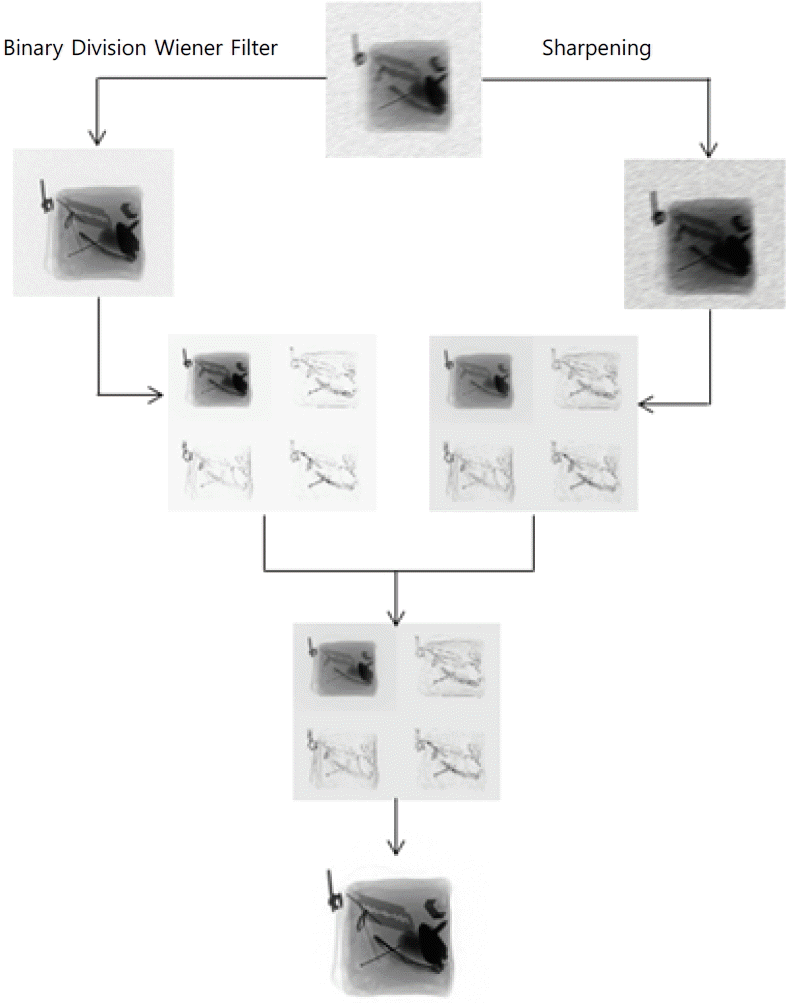
Fig. 2
Pseudo-code of boundary division with wiener filter approach. 
Fig. 3
Mean square error (MSE) values of all evaluated approaches. X-ray fused baggage image contaminated with Poisson and impulse noise with 30% noise density. BDND=boundary discriminative noise detection, SR=square-root, Elm=elimination. 
Fig. 4
Peak signal-to-noise ratio (PSNR) values of all evaluated approaches. X-ray fused baggage image contaminated with Poisson and impulse noise with 30% noise density. BDND=boundary discriminative noise detection, SR=square-root, Elm=elimination. 
Fig. 5
Mean square error (MSE) values of all these approaches. X-ray fused baggage image contaminated with Poisson and impulse noise with 90% noise density. BDND=boundary discriminative noise detection, SR=square-root, Elm=elimination. 
Fig. 6
Peak signal-to-noise ratio (PSNR) values of all these approaches. X-ray fused baggage image contaminated with Poisson and impulse noise with 90% noise density. BDND=boundary discriminative noise detection, SR=square-root, Elm=elimination. 
Appendix 1
Flow chart of boundary division wiener filter approach 
Table 1
Miss detection and false alarm
|
Noise density |
Missed detection |
False alarm |
|
BDND with SMF |
BDND with square-root |
BDND by elimination |
Proposed approach |
BDND with SMF |
BDND with square-root |
BDND by elimination |
Proposed approach |
|
30% |
12 |
9 |
7 |
3 |
2 |
2 |
0 |
0 |
|
50% |
8 |
9 |
6 |
1 |
14 |
12 |
9 |
7 |
|
90% |
16 |
13 |
11 |
2 |
23 |
19 |
16 |
3 |
Table 2
Represents time taken by all approaches during noisy pixels detection
|
Approaches |
Noise type |
Time taken (s) |
|
BDND with SMF |
Impulse noise |
17.20 |
|
Poisson noise |
16.80 |
|
Impulse/Poisson noise |
18.40 |
|
|
BDND with square-root |
Impulse noise |
15.11 |
|
Poisson noise |
16.23 |
|
Impulse/Poisson noise |
16.55 |
|
|
BDND by elimination |
Impulse noise |
17.22 |
|
Poisson noise |
17.86 |
|
Impulse/Poisson noise |
18.02 |
|
|
Proposed approach |
Impulse noise |
10.35 |
|
Poisson noise |
10.49 |
|
Impulse/Poisson noise |
10.55 |
|










