Yasmine-Derdour, Bouabdellah-Kechar, and Fayçal-Khelfi: Using Mobile Data Collectors to Enhance Energy Efficiency and Reliability in Delay Tolerant Wireless Sensor Networks
Abstract
A primary task in wireless sensor networks (WSNs) is data collection. The main objective of this task is to collect sensor readings from sensor fields at predetermined sinks using routing protocols without conducting network processing at intermediate nodes, which have been proved as being inefficient in many research studies using a static sink. The major drawback is that sensor nodes near a data sink are prone to dissipate more energy power than those far away due to their role as relay nodes. Recently, novel WSN architectures based on mobile sinks and mobile relay nodes, which are able to move inside the region of a deployed WSN, which has been developed in most research works related to mobile WSN mainly exploit mobility to reduce and balance energy consumption to enhance communication reliability among sensor nodes. Our main purpose in this paper is to propose a solution to the problem of deploying mobile data collectors for alleviating the high traffic load and resulting bottleneck in a sink’s vicinity, which are caused by static approaches. For this reason, several WSNs based on mobile elements have been proposed. We studied two key issues in WSN mobility: the impact of the mobile element (sink or relay nodes) and the impact of the mobility model on WSN based on its performance expressed in terms of energy efficiency and reliability. We conducted an extensive set of simulation experiments. The results obtained reveal that the collection approach based on relay nodes and the mobility model based on stochastic perform better.
Key words: Data Collection, MDCs, Mobility Model, Mobile Relay, Mobile Sink, Simulation, WSNs
1. Introduction
Mobile sensors are very important for the monitoring field, which can be inaccessible, unfamiliar, or even hostile, where sensors are deployed from a distance (e.g., from a safe location or from an aircraft) and then reposition themselves to provide the required sensing coverage [ 1]. These sensors are able to detect measures and bring back physical data related to their environment to make monitoring [ 2]. These sensors form wireless sensor networks (WSNs) that make it possible for the sensors to communicate with each other and to forward the data that they collect to the sink. Data collection is a fundamental task of WSNs. It aims to collect sensor readings from sensory fields at predefined sinks (without aggregating at intermediate nodes) for analysis and processing. A routing protocol must provide fast and reliable techniques for data propagation. In WSNs, the role of data routing is essential to transmitting the data collected by the sensors to the sink, but this will directly impact energy consumption. Intermediate sensors will use up energy during the reception and the transmission phases due to the relaying of a data packet. To reduce this loss of energy, it is more interesting than the sink moves to get promoting data communications at 1-hop [ 3– 6]. Obviously, this solution generates an additional delay in collecting data, but this delay is still possible in the class of delay-tolerant networks that we examine in this paper. In addition, most routing solutions for WSNs use static sinks to collect data from the entire network [ 7]. This approach results in a high traffic load in the sink’s vicinity. As such, the nodes located near the sink will be more requested for relaying data than other nodes in the network. Therefore, these nodes will consume more energy and face high congestion in a large-scale network. In this paper, we propose a solution to the problem of deploying mobile data collectors in order to alleviate the high traffic load and resulting bottleneck in a sink’s vicinity, which are caused by static approaches. For this reason, several WSNs are based on mobile elements (MEs), which propose a base of hybrid adaptive protocols for reliable data delivery in WSNs with multiple mobile sinks [ 8]. However, there are some limitations and/or drawbacks of these proposed approaches. For example, none of them has considered at the same time the two studied problems in their optimization strategy or most of them have just studied separately these two problems. The aim of our work is to consider the following two problems at the same time: 1) choosing the best mobile data collector to move inside the space area, 2) choosing the best mobility model in order to move this element. The results presented in this paper suggest recommendations for data collection in WSN applications based on mobile collectors.
Initially, we studied the choice and impact of the mobile data collector (sink and relay nodes) on WSN performances, in terms of energy efficiency, the number of received messages, and latency, by using a simulation approach. To do so we carried out extensive simulations using some scenarios that represented the two approaches for collecting data (mobile data collector [MDC] as a sink node and MDC as a relay node). Then we compared the obtained results to deduce which of these two approaches guarantees better performances in the network. All simulations have been realized by using the OMNeT++ simulator coupled with two frameworks dedicated to mobility, by using the MiXiM-INeT-Bundle, which is comprised of MiXiM and INeT.
The second goal is related to choosing the best mobility model with which the mobile element must move while gaining in energy consumption, delay, and the number of packets losses. We carried out extensive simulations under some scenarios that represented three types of mobility models (Gauss-Markov, Random Walk, and Random WayPoint) for a reliable and effective data collection. Then, we compared the results to deduce the solution that offers better results, in terms of minimizing energy consumption by the sensor nodes and reducing data loss. The simulations that were carried out for this purpose were run in the same environment.
The content of this paper is organized as follows: in Section 2, related works and theoretical background about mobile data collectors (sink or relay nodes) and mobility models are surveyed. In Section 3, we present various types of WSNs with MEs. Among the interested MEs in MDCs, two types of MDCs are proposed: sink MDCs and relay MDCs. In this section, we also address the mobility models which focus on the three mobility models that we chose for this study. Section 4 is dedicated to our first contribution in which we presents the simulation scenarios of data collection by MDCs with the parameters used in the simulation and the corresponding figures for each scenario. Our second contribution is detailed in Section 5 in which we discuss three scenarios that were simulated for choosing the best mobility model and the algorithms of mobility that we used. Simulation results and discussions for the first contribution are given in Section 6 by evaluating dissipated energy, throughput, and latency through histograms. We explain in Section 7 the performance results of each mobility model (Random Walk, Random WayPoint, and Gauss-Markov) by evaluating the number of received packets versus time. Tables, figures, and histograms are used to illustrate all of these items. Section 8 provides a discussion about the results and Section 9 give the conclusion and outlines research work that should be carried out in the future.
2. Related Work
In mobile WSNs, the following two approaches are often proposed: implementing the mobility of sensors nodes that form the network and using the mobility of data collectors that can be a sink or relay nodes. In this paper, we are more interested in WSNs with MDCs. Several research works covering this subject are proposed in the review of literature on [ 7– 9] In [ 7], the authors focus on the response delay sensitive applications, such as emergency preparedness and hostile environment surveillance, of WSNs. These applications pose challenging obstacles to the protocols for WSNs. A routing protocol must provide fast and reliable techniques for data propagation. Many studies have proposed a solution to the problem of deploying MDCs in order to alleviate the high traffic load and resulting bottleneck in a sink’s vicinity. These studies have proposed the MDC/PEQ protocol, which employs MDCs that broadcast beacons periodically. Sensor nodes that receive the beacon will join the MDC’s cluster and update their routing information in order to relay data packets to the MDC. Sensor nodes use the signal strength of the beacon in order to perform a simple but efficient route re-configuration. An extensive set of simulation experiments were conducted and the results confirm that the introduction of MDCs in WSNs reduces the bottleneck at the nodes that are closer to the sink. The researchers of this article have proposed a mobility technique for gathering data that does not introduce traffic or energy overhead. In fact, it significantly reduces traffic and, consequently, it also decreases the packet delay and energy dissipation by reducing the average number of hops that data packets have to traverse from the source sensor nodes to the sink or mobile data collectors. As we already stated above, we used the two approaches of mobile sinks and mobile relays in mobile WSNs.
MDCs as a Sink Node: this approach considers a MDC as a mobile sink in WSN, which is responsible for gathering sensed data using multi-hop communication [9]. In [10], the authors proposed a different approach that applies data collection in urban scenarios where people act as mobile sinks while gathering environmental data. The work presented in [11] examines data collection where the researchers proceeded to randomly collect data while protecting the location of mobiles sinks in the network. In [12], the authors defined scalable distributed and heuristics models for simultaneous movement and the coordinates of multiples sinks in the network. MDCs as a Relay Node: the article in [13] examines methods that allow for the reduction in a mosaic. This is where the reduction in a mosaic represents a reduction in a Voronoi mosaic, whose production points are the mass centers of Voronoi area correspondence, by using mobile relays. In [14], the authors propose a data collection method based on mobiles relays in the network with a data MULE system. This is about architecture three-thirds, where its average level of this architecture is represented by relay nodes, called Mobiles Ubiquitous LAN Extensions (MULEs). Among the most famous approaches, that of the Ferraing message, relay nodes move in network area, and data collection of the static nodes in a scattered network topology [15].
This paper makes a comparison between a mobile and static sink, among solutions to the problem of extending the lifetime of sensor nodes that are close to the sink is the data collection, which uses a mobile sink. In some aspects, this is similar to using several static sinks. However, using several static sinks requires additional global communication for collecting all of the data at a single final point [ 16, 17]. In order to overcome the shortcomings observed for a static sink, we are proposing a mobile sink approach. A mobile sink can follow different types of mobility patterns such as random mobility, predictable/fixed path mobility, or controlled mobility, in the sensor field. All of which have consequences with respect to energy efficiency and data collection strategies. In the following discussion, we summarize some proposed solutions for each type of mobility [ 17, 18]. This paper basically classifies and evaluates the mobility metrics into two categories—direct mobility metrics and derived mobility metrics. These two mobility metrics have been used to measure different mobility models. Authors consider some of mobility models (i.e., the Random WayPoint Model, the Reference Point Group Mobility Model, the Random Direction Mobility Model, the Random Walk Mobility Model, the Probabilistic Random Walk, the Gauss-Markov Mobility model, the Column Mobility Model, the Nomadic Community Mobility Model, and the Manhattan Grid Model) [ 19]. In the performance evaluation of a protocol for an ad hoc network, the protocol should be tested under realistic conditions the following areas, as well as others: a sensible transmission range, limited buffer space for the storage of messages, representative data traffic models, and realistic movements of the mobile users (i.e., a mobility model). This paper is a survey of mobility models that are used in the simulations of ad hoc networks. The researchers describe several mobility models that represent mobile nodes whose movements are independent of each other (i.e., entity mobility models), and several mobility models that represent mobile nodes whose movements are dependent on each other (i.e., group mobility models). The goal of this paper is to present a number of mobility models in order to offer researchers more informed options when they are deciding upon a mobility model to use in their performance evaluations [ 20]. Lastly, we will present simulation results that illustrate the importance of choosing a mobility model in the simulation of an ad hoc network protocol. More specifically, we will illustrate how the performance results of an ad hoc network protocol drastically change because of changing the mobility model simulated [ 21].
2.1 The Advantages of Mobility Techniques in WSNs
Some of the advantages of exiting techniques cited in related work are as listed below.
Connectivity: because nodes are mobile, a dense WSN architecture may be not a requirement. Cost: since fewer nodes can be deployed, the network cost is reduced in a mobile WSN. Reliability: since traditional (static) WSNs are dense and the communication paradigm is made up of multi-hops reliability which is compromised of interference and collisions. Energy Efficiency: the traffic pattern inherent to WSNs is convergecast, that is, messages are generated from the sensor nodes and are collected by the sink. Prolong Network: the lifetime of the network and decreases the latency under the appropriate parameters.
2.2 The Disadvantages of Mobility Techniques in WSNs
Contact Detection: since communication is only possible when the nodes are in transmission range of each other, it is necessary to detect the presence of a mobile node correctly and efficiently. Mobility-Aware Power Management: in some cases, it is possible to exploit the knowledge about the mobility pattern to further optimize the detection of mobile elements. Reliable Data Transfer: as available contacts might be scarce and short, there is a need to maximize the number of messages that are correctly transferred to the sink. Mobility Control: when the motion of mobile elements can be controlled, a policy for visiting nodes in the network has to be defined [7,8].
3. Mobility and WSNs
Depending on the elements constituting the network, we distinguish two types of WSNs, which are stationary and mobile WSNs [ 22].
Stationary WSNs: a stationary WSN consists of stationary sensors nodes that monitor the occurrence of events in a given geographical area [23]. Sensor nodes only perform monitoring and the sent measured data uses multi-hop routing to communicate with the sink. Mobile WSNs: a mobile WSN is a traditional WSN where one or several elements are moving in a stationary environment. The purpose of this type of network is in most of time the exploration of inaccessible and dangerous areas, or to reduce the energy consumption of sensor nodes in the data collection process, in order to prolong the lifetime of the network [7].
To better understand the specific features of WSN with mobile elements (WSN-MEs), let us first introduce the reference network, which is conducted according to the role of the MEs.
The main components of WSN-MEs are as described below.
Regular sensor nodes (nodes for short): these are the sources of information. These nodes perform sensing as their main task. They may also forward or relay messages in the network, depending on the adopted communication paradigm. Sinks (base stations): these are the destinations for information. They collect the data sensed by sensor nodes either directly (i.e., by visiting sensors and collecting data from each of them) or indirectly (i.e., through intermediate nodes). They can use data coming from sensors autonomously or make them available to interested users through an Internet connection. Special support nodes: these perform a specific task, such as acting as intermediate data collectors or mobile gateways. They are not sources nor are they the destinations for messages, but they exploit mobility to support network operation or data collection [8].
Different types of MEs with increasing level of mobility, and by focusing on architectural aspects are given in the Table 1. We are interested in our work on MDCs. These are MEs that visit the network to collect data generated from source nodes. Depending on how they manage the collected data, MDCs can be either mobile sinks or mobile relays.
Mobile sinks (MSs): these are mobile nodes, which are the destination for messages that have been originated by the sensors, that is, they represent the endpoints of data collection in WSN-MEs. They can either autonomously consume collected data for their own purposes or make them available to remote users by using a long-range wireless Internet connection. Mobile relays (MRs): these are support nodes, which gather messages from sensor nodes, store them, and carry the collected data to sinks or base stations. They are not the endpoints of communication. They only act as mobile forwarders. This means that the collected data moves with them until the MR comes into contact with the sink or base station [8].
We are also interested in this paper at the same time in the choice of the best mobility model according to which we must move this element.
There exist several mobility models that propose movement strategies for the sensors. In addition, there exist models that deal with the displacement of all of the nodes, and others that deal with only one node. The first family of models is called the Exponential Correlated Random Mobility Model (ECRMM), Nomadic Community Mobility Model (NCMM), Reference Point Group Mobility Model (RPGMM) [ 24, 25]. The second family is the mobility of the entity, which is our main concern in this study.
3.1 The Entity Mobility Models
Several mobility models exist (see the classifications given in Table 2), but in our paper, we are presenting four entity mobility models for the performance evaluation of a WSN. The two models presented are the Random Walk Mobility Model (RWMM) and the Random WayPoint Mobility Model (RWPMM), which are widely used in practice. The two others are the Gauss-Markov Mobility Model and the City Section Mobility Model (CSMM) [ 21, 26, 28].
4. Simulation Scenarios of Data Collection by MDCS “Contribution 1”
We developed the following five scenarios: one mobile sink (1-MS), one mobile relay (1-MR), two mobile relays (2-MR), four mobile relays (4-MR), and a stationary wireless sensor network (S-WSN). All of which we applied to a network established by twenty sensor nodes, next to the sink. Sensor nodes were organized in a grid architecture with a 4×5 dimension. Sensor nodes are arranged in the empty columns of the grid, except for the scenario 1-MR, where we opted for a linear architecture.
In these scenarios, we always took into consideration that all elements of the network are nodes implementing the IEEE 802.15.4 protocol and are powered with a battery. The batteries of sensor nodes have a limited load; whereas, relay nodes and the sink are powered with unlimited energy. Sensor nodes exchange gathered information via a one-hop communication using a flooding mechanism as a routing protocol, which we used to suit the needs of our work.
Parameter values, which used all simulated scenarios, are summarized in the Table 3.
4.1 Scenarios Simulated with 1-MS MDCs
In this configuration, the sink is mobile, whereas, the rest of the nodes are stationary. The mobile sink MDCs crosses columns of the grid where the nodes are deployed, while collecting information, as illustrated in Fig. 1(a).
4.2 Scenarios Simulated with 1-MR MDCs
This approach differs from the previous one by the use of the second type of MDC, which is the node relay. Therefore, we chose to move one or several relay nodes instead of the sink. The values of the network parameters are the same, with the exception of the parameter ‘type of nodes’, where we used Host 802.15.4 node sensors, which has a simple battery with a higher storage capacity.
4.3 Scenarios Simulated with 2-MR MDCs
In this scenario, we chose another method for collecting data. The idea was to split the network into two parts for collecting data. The latter consists of 18 stationary sensor nodes, a stationary sink, and two mobile relays. Each of the node relays assures that the collected data is only captured by the area of the nodes. These relays make a visit of data collection in the area where they operate, collect data, and then join the sink to broadcast them to him. The trajectory borrowed by each of the relay nodes is illustrated in Fig. 1(c).
4.4 Scenarios Simulated with 4-MR MDCs
We used a network that was divided into four collection parts. This network consists of 16 sensor nodes, a S-WSN, and 4-MR. Each of these nodes assures in its trajectory that the collected data is only captured by the sensor nodes. The model of mobility chosen in this case promotes movement in straight line, which is shown in Fig. 1(d).
4.5 Scenarios Simulated with a S-WSN
In this work, we envisioned a single solution of S-WSN scenario, with the aim of comparing the results obtained from it with those obtained from the scenarios using a mobile WSN. The network is composed of 20 sensors nodes and a single sink where all of the elements are stationary. Contrary to the solutions using 1-hop mobile WSN, the communication between sensor nodes and the sink is multi-hop.
Parameters of this configuration are the same as those presented in Table 3, except the used routing scheme, which is ‘wise-route’ instead of ‘flooding’.
5. Simulated Scenarios and Mobility Algorithms for Choosing the Best Mobility Models “Contribution 2”
The simulated network consists of a set of fixed sensors (N sensors) and only one mobile sink. The sink ensures that data collection is sent periodically according to the simulated application. These details will be discussed with regard to every scenario in the following sections. Fig. 2 shows the various components of the network. Several execution scenarios were tested. For each of them we changed the mobility model, the sink’s speed, the simulation time, and the number of sensors. The scenarios postpone one of the other one by:
The number of sensors in the network The type of sink mobility The simulation time The sink’s speed The number of radio channel in the sink: this parameter was varied in order to be able to put sensor sets in different collision fields. Consequently, we have chosen to focus on data collection without the influence of packets loss due to a collision.
We tested four mobility models on networks containing three and 10 sensors with different displacements velocities.
5.1 Scenarios Simulated
Scenario 1: Table 4 represents the various simulation parameters for Scenario 1. Scenario 2: in this scenario, we included the same parameters for simulation as Scenario 1, except that we changed the number of sensors and the simulation time. Table 5 shows the values of the modified parameters. Scenario 3: After running various scenarios by changing the number of sensors and the mobility model in the previous scenarios. Then, we studied how changing the displacement speed impacted data collection from the three mobility models with 10 sensors.
5.2 MobilityAlgorithms
There are several mobility models that have been proposed by other researchers and each of them has its own characteristics, advantages, and disadvantages. In spite of their diversity, the majority of mobility algorithms are stochastic. In this section, we describe the three algorithms for the various mobility models that we have chosen.
Algorithm 1
Random WayPoint Model [ 21]
|
1: |
Long Play_Ground_x=600 |
|
2: |
Long play_Ground_y=400 |
|
3: |
Long Position_X=uniform(0, Play_Ground_x) |
|
4: |
Long Position_Y=uniform(0, Play_Ground_y) |
|
5: |
IntPause_time=30 ; |
|
6: |
While(!Stop Condition) |
|
7: |
{ |
|
8: |
Long target_X==uniform(0, Play_Ground_x) |
|
9: |
Long target_Y=uniform(0, Play_Ground_y) |
|
10: |
Move(Position_X, Position_Y, target_X, target_Y) ; |
|
11: |
Position_X=target_X |
|
12: |
Position_Y=target_Y |
|
13: |
Pause(Pause_time) |
|
14: |
} |
Algorithm 2
Random Walk Model [ 21, 29]
|
1: |
Long Play_Ground_x=600 |
|
2: |
Long play_Ground_y=400 |
|
3: |
Long Position_X=uniform(0, Play_Ground_x) |
|
4: |
Long Position_Y=uniform(0, Play_Ground_y) |
|
5: |
While(!Stop Condition) |
|
6: |
{ |
|
7: |
Long target_X==uniform(0, Play_Ground_x) |
|
8: |
Long target_Y=uniform(0, Play_Ground_y) |
|
9: |
Move(Position_X, Position_Y, target_X, target_Y) ; |
|
10: |
Position_X=target_X |
|
11: |
Position_Y=target_Y |
|
12: |
} |
Algorithm 3
Gauss-Markov Model [ 26, 27]
|
1: |
play_Ground_x=600 |
|
2: |
play_Ground_y=400 |
|
3: |
Long position_x=uniform(0, play_Ground_x) |
|
4: |
Long position_y=uniform(0, play_Ground_y) |
|
5: |
Inttemps_pause; |
|
6: |
While (stop condition not reachable) { |
|
7: |
Long x_temp=position_x+velocity*cos(direction) |
|
8: |
Long y_temp=position_y+velocity*sin(direction) |
|
9: |
Long normal_velocity=random(0,1); |
|
10: |
Long normal_direction=random(0,1); |
|
11: |
Long velocity_temp=alpha*velocity+(1-alpha)*mean_velocity+sqrt(1-alpha au carré)*normal_velocity; |
|
12: |
Long directetion_temp=alpha*vct_direction+(1-alpha)*mean_direction+sqrt(1-alpha aucarrée)* normal_direction//gestion des bordures |
|
13: |
if (x_temp<dist_bord) { mean_direction =0;} |
|
14: |
if (x_temp>play_Ground_x-dist_bord) { mean_direction =180;} |
|
15: |
if (y_temp<dist_bord) { mean_direction =90;} |
|
16: |
} |
6. The Results the Analysis of Contribution 1
The results obtained from the MDCs data collection scenarios will be explained in this section. 1-MS, 1-MR, 2-MR, 4-MR, and S-WSN are summarized in Table 6. In these scenarios, we considered three network performance parameters, namely, dissipated energy, lost messages, and latency. These parameters are calculated as explained below.
The dissipated energy by the network (Ed) calculated by the following formula:
The lost messages (Throughput) are calculated as follows:
The latency (Lat) is calculated by the formula:
6.1 Evaluation of the Energy
Using a histogram, as illustrated by Fig. 3, can represent the four results obtained from the execution of scenarios that are relative to the mobile WSN, which are shown in Table 6. According to the results presented in Table 6 and Fig. 3, we notice that the energy dissipated by the sensor nodes in various configurations are given in increasing order as follows: 4-MR < 1-MS < 2-MR < 1-MR < S-WSN.
6.2 Evaluation of Lost Messages
The results obtained by the execution of scenarios related to the mobile WSN are depicted in Fig. 4. The results concerning the lost messages obtained and illustrated in the Fig. 4 allow the following classification. The number of lost messages in the network is given by increasing order, as follows: 4-MR < 2-MR < 1-MS < S-WSN < 1-MR.
6.3 Evaluation of Latency
The third parameter that we used in our study is latency. It is calculated as being the time that has passed between the generation of the message and its reception by the sink (collector). The results obtained from these parameters are illustrated in Fig. 5. The values relative to the latency obtained in the simulated scenarios are given in increasing order as follow: S-WSN < 4-MR < 2-MR < 1-MS < 1-MR.
7. The Results the Analysis of Contribution 2
7.1 Results and Discussion of Scenario 1
The results of scenario 1 are shown in Table 7. The four images of Fig. 6 show the evolution of the number of packets received according to the time variation for the 4 considered mobility models. In the Circle Mobility model, the sink turns at a constant speed in a circle of radius X, which enables it to visit the three sensors periodically. For doing so, the sink has a precise time in the capture zone of the sensor. This can be an advantage and a disadvantage for this model at the same time. The advantage is that information will be equally acquired by the three sensors where we can see an increased number of received messages periodically, which is shown in Fig. 6(a). On the other hand, it becomes a disadvantage if an area that is specified from a simulation contains more events than another, whereas, a sink is only reachable for one precise period. Furthermore, no collision takes place because the sensors are spread in such a way that none of them returns in the collision domain of the other sensor node. For the Gauss-Markov Model, the directed random movement of sink in relativity to its old position makes it possible to receive the maximum number of messages because it does not immediately revisit a sensor that it has just visited. The number of received packets increases more quickly than the previous model ( Fig. 6(b)). This is due to the directed random movement of the Gauss-Markov Model. The Random Waypoint Model is a model with random movement, therefore, the sink moves randomly in the deployment space, and marks a pause once it arrives at its destination. This explains the fragmentation of the graph illustrated in Fig. 6(c). The sink returns in the sensor radio area and then comes out from this area randomly. The Random Walk Model is similar to the Random WayPoint Model, except that it is less stable in the absence of pause time. Once it returns to the radio area, it leaves. Its behavior cannot be predicted or explained during the simulation time, as illustrated in Fig. 6(d).
Comparison Between the Four Mobility Models
In the histogram shown in Fig. 7, the four mobility models, Gauss-Markov and Random WayPoint are the models that give the best results in terms of packets received and lost. On the other hand, the Random Walk Model is a purely random model and it can give poor results due to its stochastic nature.
7.2 Results and Discussion of Scenario 2
The results of Scenario 2 are described in Table 8. The three figures show the evolution of the number of packets received according to the time variation for the 4 considered mobility models. In the first model, the circular motion of the sink becomes a bottleneck. Here, the sink always revisits the same sensors with each round. Therefore, it is unaware of other sensors that are carrying information. Consequently, the sink will not be able to collect the data of certain sensors.
For the Gauss-Markov Model, the existence of several simultaneous exchanges of information resulted in the appearance of collisions, which automatically implies that the application of the algorithm of Back. This explains the late reception of data by the sink (until the 10th second of simulation). On the other hand, the data collection as from the 10th second increases significantly as shown in Fig. 8(a). The Random WayPoint Model has fewer occurrences of collisions than the other models. This is due to the time of pause, which is made on the level of each sensor. However, in certain cases, it can become a bottleneck if the sink is within radio range of several sensors at the same time during its pause time. This can lead to collisions on several occasions.
On the other hand, the Random Walk Model with several sensors allows for a good amount of information retrieval thanks to its stochastic aspect.
Comparison Between the Four Mobility Models
As depicted by Fig. 9, the Circle Mobility Model gives poor results compared to the other models. This is the case for all of the models where the trajectory is predefined in advance. The sink revisits the same sensors each time. This kind of model can become interesting if the sensors are deposited on their way to the sink. On the other hand the models containing random movements always maintain their good performances.
7.3 Results and Discussion of Scenario 3
The results of Scenario 3 are given in the Table 9 and Fig. 10. On the other hand we observed that the two models (Gauss Markov and WayPoint) gave good performances compared to the model walk for the received packets, which is a bad result for the lost packet. In the interval (4 m/s, 10 m/s) the three models provide good performances for the quantity of received packets. On the other hand, the number of lost packets increases. In the interval (10 m/s, 15 m/s) the three models provide bad results. We observed that both the Gauss Markov and Random Walk Models lost many packets and the Random WayPoint Model recorded less lost packets. This is due to its pause time carrying out during each displacement. In addition, the reception of the packets decreased for the three models, and this is due to the increase in the displacement speed. Therefore, the sink could not receive all of the packets.
Thus, the three models at the mean speed have better results compared to the models where the speed is low or high. This is because a model at a low speed visits fewer sensors than a model with a higher speed.
8. Discussion
About a compromise between performances of scenario selected through our study and the corresponding economic cost, some critical applications such as ‘search and rescue’ (e.g., rescue of survivors after an earthquake, tsunami or flood), where the presence of multiple mobile robots is inevitable in order to perform a reliable data collection to facilitate operations of intervention in timely manner. Thus, the investment cost in mobile elements is justified in this case. However, in other applications where an emergency is not a fundamental constraint (e.g., environmental monitoring, agriculture, health monitoring of structures, etc.), having just one mobile element in this case is reasonable and presents an economic solution.
9. Conclusion and Future Work
According to the obtained results, it is clear that the methods based on the MDCs consume much less energy than the static method (stationary). Therefore, in the mobile WSNs, we observe clearly that the ‘4-MR’ scenario allows to conserve more energy and guarantees a greater reliability in transferring messages, as well as less latency. Nevertheless, it should be noted that the static method offers a significant latency with regard to that of the MEs. Thus, the selection of the best data collection method according to its area of usage allows for a significant gain in terms of latency and energy. In our case, we were more interested in the energy dissipated by the network during the data collection process. Thereby, we can deduce that the configuration based on the MDCs of mobile relays is the most appropriate for the energy efficiency of sensor nodes in the network, particularly, in the case of four mobile relays. The performances of analysis that we are concerned with in this paper is the mobile element, which is connected to the sensor nodes (limited battery). Unfortunately, saving energy by using the mobility paradigm that generates another challenging problem, which is latency (the significant transmission delay of the data packets). This drawback does not raise a problem in the context of our study because we carried out operations on border surveillance applications in a safe scenario (i.e., where an alert event can be well managed by border authorities). However, for delay sensitive applications, we intend to propose a compromise solution between energy consumption and latency. The models containing random movement provide better results compared to ratios to the models may be defined in advance with a mean velocity to give a better result.
As for future work, we intend to simulate a wireless sensor network, including mobile sensors with a mobility model of groups, and mobile sink by a mobility model of entity. Another area that needs to be further developed is to test other complex mobility models that have been discussed in other studies and to carry out practical achievements by using a robot navigator that will play the part of the sink.
Biography
She is a teacher in the Department of Computer Science at Oran University, Algeria. Where she received her MS degree (Magister) in computer science in 2010. She is a Ph.D. candidate at final stage. She is also a research member at the Laboratory of Research in Industrial computing and networking. She has published eight papers in refereed conference proceedings (IEEE and Elsevier) and two publications in the journals. Her current research area focuses on wireless sensor networks with mobile sink, energy consumption, performance and security in wireless sensor networks.
Biography
He is an Assistant Professor in the Department of Computer Science at Oran University, Algeria where he received his Ph.D. in 2010. He has authored several journal publications, refereed conference publications and one book chapter. He has been a member of the technical program and organizing committees of several international IEEE/ACM conferences and workshops. His current research interests include mobile wireless sensor/actuator networks, Zigbee/IEEE 802.15.4 technologies deployment, vehicular sensor networks and heterogeneous wireless networks, with special emphasis on radio resource management techniques, performance modeling, provisioning QoS and practical societal and industrial applications.
Biography
He received Ph.D. degree in Automatic Control from Nancy University, France, in 1995. He is currently Professor at the Computer Science Department - Faculty of Exact and Applied Sciences - University of Oran 1 Ahmed Ben Bella - Algeria. He is also a research member at the Laboratory of Research in Industrial Computing and Networks. His main research interests include Automatic Control, Industrial Computing, Robotics and Artificial Intelligence.
References
1. N. Bartolini, T. Calamoneri, TL. Porta, and S. Silvestri, "Mobile sensor deployment in unknown fields," in Proceedings of the 29th IEEE International Conference on Computer Communications (INFOCOM2010), San Diego, CA, pp. 471-475, 2010.  2. A. Chamam, in Optimized mechanisms of planning of the sensors states for the maximization of the lifetime in the wireless sensors networks, Polytechnic School of Montreal, 2009.
3. ME. Keskın, İK. Altınel, N. Aras, and C. Ersoy, "Lifetime maximization in wireless sensor networks using a mobile sink with nonzero traveling time," The Computer Journal, vol. 54, no. 12, pp. 1987-1999, 2011.  4. Q. Dong, and W. Dargie, "Performance analysis of a handover mechanism for a mobile wireless sensor network," in Proceedings of IEEE Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, pp. 645-648, 2013.
5. GS. Sara, and D. Sridharan, "Routing in mobile wireless sensor network: a survey," Telecommunication Systems, vol. 57, no. 1, pp. 51-79, 2014.  6. Y. Hu, Y. Ding, K. Hao, L. Ren, and H. Han, "An immune orthogonal learning particle swarm optimisation algorithm for routing recovery of wireless sensor networks with mobile sink," International Journal of Systems Science, vol. 45, no. 3, pp. 337-350, 2014.  7. RWN. Pazzi, and A. Boukerche, "Mobile data collector strategy for delay-sensitive applications over wireless sensor networks," Computer Communications, vol. 31, no. 5, pp. 1028-1039, 2008.  8. M. Di Francesco, SK. Das, and G. Anastasi, "Data collection in wireless sensor networks with mobile elements: a survey," ACM Transactions on Sensor Networks, vol. 8, no. 1, article no. 7, 2011.  9. G. Anastasi, E. Borgia, M. Conti, and E. Gregori, "A hybrid adaptive protocol for reliable data delivery in WSNs with multiple mobile sinks," The Computer Journal, vol. 54, no. 2, pp. 213-229, 2011.  10. I. Chatzigiannakis, A. Kinalis, and S. Nikoletseas, "Efficient data propagation strategies in wireless sensor networks using a single mobile sink," Computer Communications, vol. 31, no. 5, pp. 896-914, 2008.  11. ECH. Ngai, and I. Rodhe, "On providing location privacy for mobile sinks in wireless sensor networks," Wireless Networks, vol. 19, no. 1, pp. 115-130, 2013.  12. S. Basagni, A. Carosi, C. Petrioli, and CA. Phillips, "Coordinated and controlled mobility of multiple sinks for maximizing the lifetime of wireless sensor networks," Wireless Networks, vol. 17, no. 3, pp. 759-778, 2011.  13. T. Imaizumi, H. Murakami, and Y. Uchimura, "Deployment control of wireless multihop-relay mobile robots based on Voronoi partition," Electrical Engineering in Japan, vol. 184, no. 4, pp. 42-51, 2013.  14. S. Jain, RC. Shah, W. Brunette, G. Borriello, and S. Roy, "Exploiting mobility for energy efficient data collection in wireless sensor networks," Mobile Networks and Applications, vol. 11, no. 3, pp. 327-339, 2006.  15. W. Zhao, M. Ammar, and E. Zegura, "A message ferrying approach for data delivery in sparse mobile ad hoc networks," in Proceedings of the 5th ACM International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc’04), Tokyo, Japan, pp. 187-198, 2004.  16. E. Lee, S. Park, J. Lee, S. Oh, and SH. Kim, "Novel service protocol for supporting remote and mobile users in wireless sensor networks with multiple static sinks," Wireless Networks, vol. 17, no. 4, pp. 861-875, 2011.  17. MI. Khan, WN. Gansterer, and G. Haring, "Static vs Mobile sink: the influence of basic parameters on energy efficiency in wireless sensor networks," Computer Communications, vol. 36, no. 9, pp. 965-978, 2013.  18. J. Luo, J. Panchard, M. Piorkowski, M. Grossglauser, and JP. Hubaux, "Mobiroute: and routing towards a mobile sink for improving lifetime in sensor networks," in Distributed Computing in Sensor Systems, Heidelberg: Springer, 2006, pp. 480-497.  19. S. Kumar, SC. Sharma, and B. Suman, "Classification and evaluation of mobility metrics for mobility model movement patterns in mobile Ad-Hoc networks," International Journal on Applications of Graph Theory in Wireless Ad Hoc and Sensor Networks (GRAPH-HOC), vol. 3, no. 3, pp. 25-38, 2011.  20. T. Camp, J. Boleng, and V. Davies, "A survey of mobility models for ad hoc network research," Wireless Communications and Mobile Computing, vol. 2, no. 5, pp. 483-502, 2002.  22. N. Bendimered, "Dymo multiple-ways with disjoined nodes without interferences for Zigbee/Standard IEEE 802.15.4 network,"Master’s thesis, University of Oran; Algeria: 2010.
24. JL. Huang, and MS. Chen, "On the effect of group mobility to data replication in ad hoc networks," IEEE Transactions on Mobile Computing, vol. 5, no. 5, pp. 492-507, 2006.  25. V. Lenders, J. Wagner, and M. May, "Analyzing the impact of mobility in ad hoc networks," in Proceedings of the 2nd International Workshop on Multi-hop Ad Hoc Networks: from Theory to Reality (REALMAN’06), Florence, Italy, pp. 39-46, 2006.  26. L. Chen, and WB. Heinzelman, "A survey of routing protocols that support QoS in mobile ad hoc networks," IEEE Network, vol. 21, no. 6, pp. 30-38, 2007.  27. B. Liang, and ZJ. Haas, "Predictive distance-based mobility management for PCS networks," in Proceedings of the 18th Annual Joint Conference of the IEEE Computer and Communications Societies (INFOCOM’99), New York, NY, pp. 1377-1384, 1999.  28. V. Tolety, "Load reduction in ad hoc networks using mobile servers,"Master’s thesis, Department of Mathematical and Computer Sciences; Colorado School of Mines: 1999.
29. P. Bracka, "A mobility control architecture for routing messages in large ad-hoc networks,"Ph.D. dissertation, University of Marne la Vallée; France: 2011.
Fig. 1
The wireless sensor network scenarios with four types of mobile elements: (a) one mobile sink, (b) one mobile relay, (c) two mobile relays, and (d) four mobile relays. 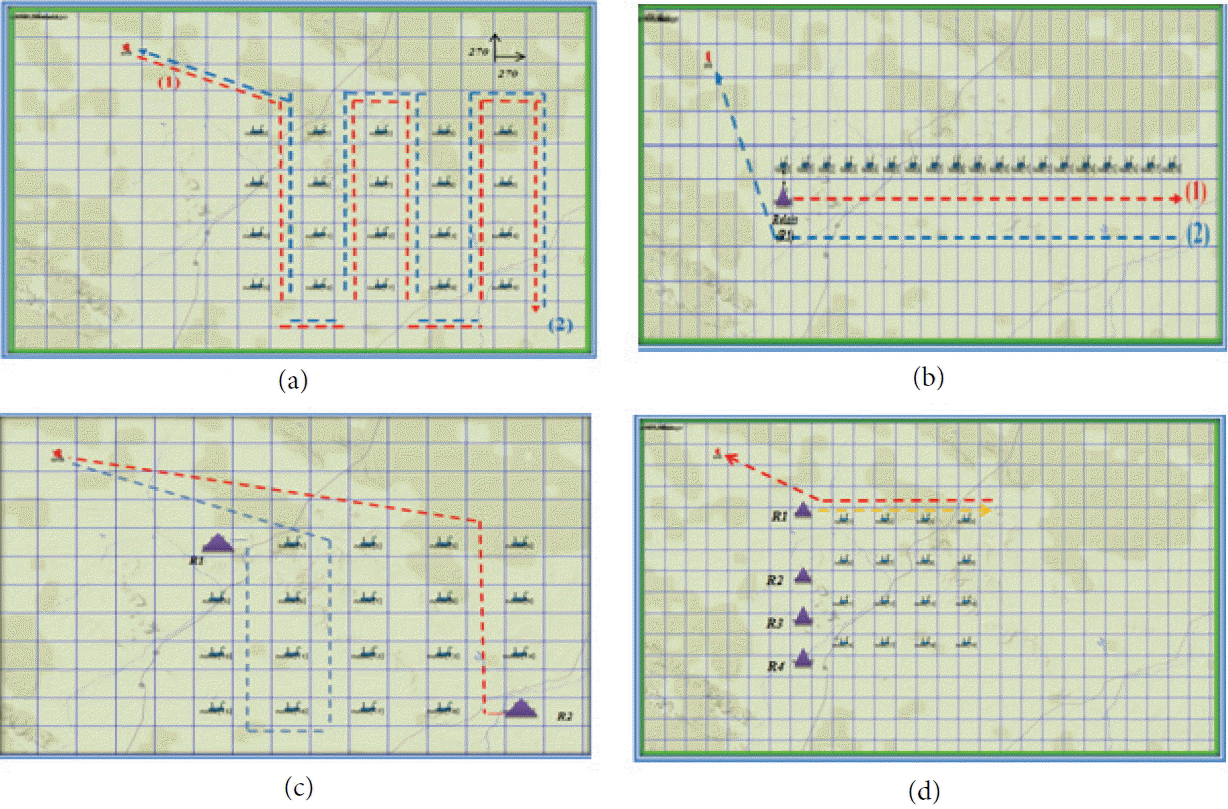
Fig. 2

Fig. 3
Energy dissipation in various realized scenarios. MS=mobile sink, S-WSN=stationary wireless sensor network. 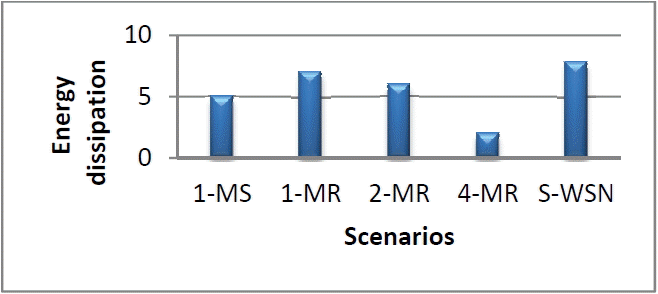
Fig. 4
Histogram representing the number of lost messages. MS=mobile sink, S-WSN=stationary wireless sensor network. 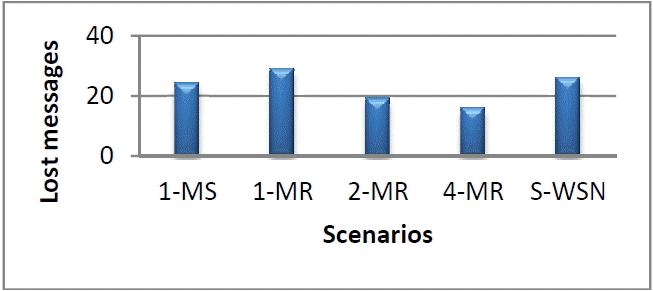
Fig. 5
Histogram representing the latency of data messages. MS=mobile sink, S-WSN=stationary wireless sensor network. 
Fig. 6
Number of received packets/time of four mobility models. (a) Circle Mobility, (b) Gauss Markov, (c) Random WayPoint, and (d) Random Walk. 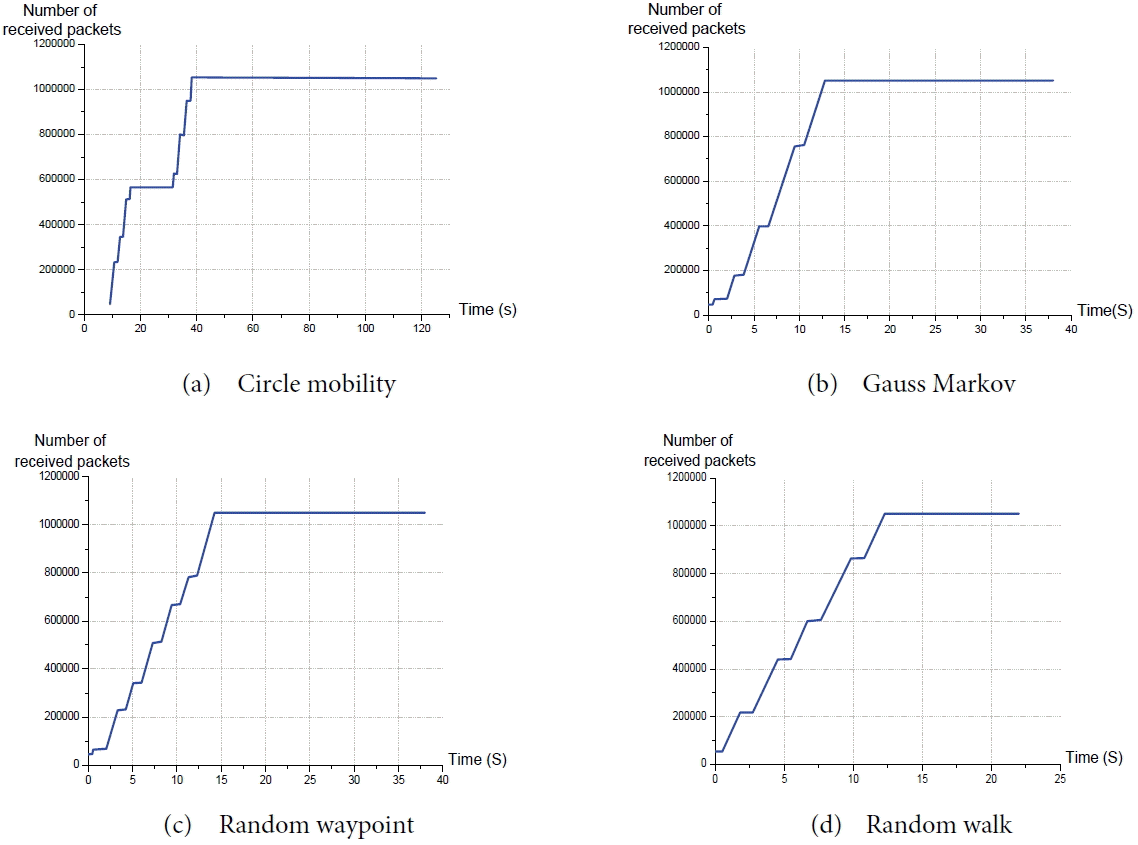
Fig. 7
The comparison between four mobility models. 
Fig. 8
Number of received packets/time of three mobility models.(a) Gauss Markov, (b) Random WayPoint, and (c) Random Walk. 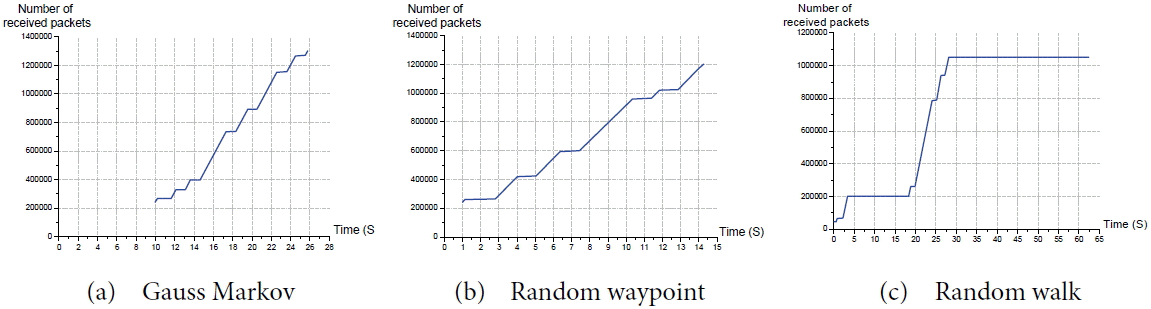
Fig. 9
Data collection with four mobility models. 
Fig. 10
The comparison between four mobility models. 
Table 1
Classification of mobile elements
|
Type of ME, Characteristics |
Relocatablenodes |
Mobile peers |
Mobile data collectors |
|
Description |
Some mobiles nodes change their location |
All nodes of networks are mobiles |
Sinks and/or relays nodes are mobiles |
|
Interest of the mobility |
Ensure better coverage and connectivity in the network |
Data collection |
Data collection for minimizing the energy consumption and for extending the network lifetime |
|
Changing network topology |
Yes |
Yes |
Case of mobile sink: no
Case of mobile relay: yes |
Table 2
Classification of mobility models
|
Mobility models |
Random speed |
Random direction |
Realist |
Type of applications |
|
Entity |
|
RWMM |
Yes |
Yes |
Yes |
Brownian movement |
|
RWPMM |
Yes |
Yes |
Yes |
WLAN |
|
Gauss-Markov |
Yes |
No |
Little |
Personnel communications services |
|
CSMM |
Yes |
No |
Yes |
Traffic regulation |
|
|
Group |
|
ECRMM |
Yes |
No |
No |
- |
|
NCMM |
Yes |
No |
Yes |
Tourist visit |
|
RPGMM |
Yes |
Yes |
Yes |
Help situation |
Table 3
Values of the parameters used in the various scenarios
|
Parameter |
Values |
|
Number of generated packets |
10 |
|
Types of applications |
« SensorApplLayer » |
|
Nominal power of battery |
99999 mAh |
|
Capacity of the battery |
99999 mAh |
|
Voltage of the battery |
3.3 V |
|
Speed of mobile data collector |
100 mps/5000 mps |
Table 4
The simulation parameters for Scenario 1
|
Models of mobility |
Circle Mobility |
Gauss Markov |
Random WayPoint |
Random Walk |
|
Number of sensors |
3 |
3 |
3 |
3 |
|
Routing protocols |
AODV |
AODV |
AODV |
AODV |
|
Mac layer |
IEEE802.11a |
IEEE802.11a |
IEEE802.11a |
IEEE802.11a |
|
Type of applications |
TCP Session APP |
TCP Session APP |
TCP Session APP |
TCP Session APP |
|
Type of communication |
Sensor->Sink |
Sensor->Sink |
Sensor->Sink |
Sensor->Sink |
|
Simulation time (s) |
500 |
500 |
500 |
500 |
|
Displacement speed (m/s) |
10 |
10 |
(1, 10) |
(1, 10) |
Table 5
The simulation parameters for Scenario 2
|
Mobility model |
Circle Mobility |
Gauss Markov |
Random WayPoint |
Random Walk |
|
Number of sensors |
10 |
10 |
10 |
10 |
|
Simulation time (s) |
100 |
100 |
100 |
100 |
Table 6
Summary of the simulation results
|
Latency (s) |
Lost messages |
Energy-dissipated (mW) |
|
1-MS |
14,06 |
24 |
62.038598009923 |
|
1-MR |
16,42 |
29 |
62.038706562718 |
|
2-MR |
3,79 |
19 |
62.038665262718 |
|
4-MR |
1,5 |
16 |
62.037237836023 |
|
S-WSN |
1,07 |
26 |
62.500000018296 |
Table 7
Results of scenario simulation 1
|
Mobility model |
Circle Mobility |
Gauss Markov |
Random WayPoint |
Random Walk |
|
Number of received packet |
5615 |
5704 |
11 |
6300 |
|
Number of lost packet |
71 |
225 |
180 |
550 |
|
Number of collisions |
0 |
2 |
0 |
2 |
Table 8
Results of scenario simulation 2
|
Mobility model |
Circle Mobility |
Gauss Markov |
Random WayPoint |
Random Walk |
|
Number of received packet |
113 |
1980 |
1969 |
1990 |
|
Number of lost packet |
638 |
158 |
78 |
53 |
|
Number of collision |
35 |
10 |
17 |
3 |
Table 9
Results of scenario simulation 3
|
(1 m/s, 4 m/s) |
4 m/s |
(4 m/s, 10 m/s) |
10 m/s |
(10 m/s, 20 m/s) |
15 m/s |
|
RW |
RWP |
GM |
RW |
RWP |
GM |
RW |
RWP |
GM |
|
Number of received packet |
1105 |
2231 |
2147 |
3217 |
3325 |
3115 |
1300 |
1750 |
1120 |
|
Number of lost packet |
30 |
20 |
35 |
87 |
83 |
77 |
195 |
125 |
251 |
|
Number of collisions |
3 |
17 |
11 |
2 |
19 |
9 |
2 |
18 |
8 |
|
Simulation time (s) |
200 |
200 |
200 |
200 |
200 |
200 |
400 |
200 |
200 |
|












