Ammar, Mebarka, Abdelmalik, and Salah: Evaluation of Histograms Local Features and Dimensionality Reduction for 3D Face Verification
Abstract
The paper proposes a novel framework for 3D face verification using dimensionality reduction based on highly distinctive local features in the presence of illumination and expression variations. The histograms of efficient local descriptors are used to represent distinctively the facial images. For this purpose, different local descriptors are evaluated, Local Binary Patterns (LBP), Three-Patch Local Binary Patterns (TPLBP), Four- Patch Local Binary Patterns (FPLBP), Binarized Statistical Image Features (BSIF) and Local Phase Quantization (LPQ). Furthermore, experiments on the combinations of the four local descriptors at feature level using simply histograms concatenation are provided. The performance of the proposed approach is evaluated with different dimensionality reduction algorithms: Principal Component Analysis (PCA), Orthogonal Locality Preserving Projection (OLPP) and the combined PCA+EFM (Enhanced Fisher linear discriminate Model). Finally, multi-class Support Vector Machine (SVM) is used as a classifier to carry out the verification between imposters and customers. The proposed method has been tested on CASIA-3D face database and the experimental results show that our method achieves a high verification performance.
Key words: 3D Face Verification, Depth Image, Dimensionality Reduction, Histograms Local Features, Local Descriptors, Support Vector Machine
1. Introduction
During the last two decades, automatic face recognition and verification have been one of the most interesting and important task in the field of computer vision due to their various applications such as, criminal identification, surveillance systems, access control, human-computer-interface, and human-robot-interaction, etc. Obtaining high recognition performance in real-world is an open problem with many face verification applications. Unfortunately, the uncontrolled conditions such as illumination variations, occlusion, facial expression, and pose variations adversely affect the performance of two-dimensional face recognition systems, which are based on 2D (color) images; this kind of information mainly depends on the light sources. More recently, various researches based on 3D images have been proposed and obtained more accuracy with these challenges [ 1– 5]. In this paper, we use the depth image which represents the geometric features of human faces, due to their several advantages over 2D intensity images in dealing with illumination variations [ 1, 2]. Facial image representation is an important process for the effectiveness of the face verification system, in which the appropriate information is obtained to be invariant in the presence of several challenges such as, illumination and facial expression variations. Among the various methods of image representation, local descriptors have been considered as one of the most successful methods adapted for this purpose. Facial image representation based on local descriptors is largely used for face recognition systems [ 6– 9]. The main idea of local descriptors is to represent the facial images discriminatively with their significant local features. Local Binary Patterns (LBP) and Local Phase Quantization (LPQ) are the best and most recent local feature based methods [ 6, 9]. LBP is an excellent operator used in face recognition system [ 6, 10]. Furthermore, LBP histograms have become a popular technique for face recognition due to their simplicity, computational efficiency, and robustness against illumination variations [ 11]. Several extended algorithms based on LBP are proposed in the literature and Three-Patch Local Binary Patterns (TPLBP) and Four-Patch Local Binary Patterns (FPLBP) are two successful LBP variants methods proposed by [ 10]. In this paper, an efficient 3D face verification is proposed using 3D depth images based on the LBP method and their variants TBLBP and FPLBP. Moreover, LPQ and BSIF (Binarized Statistical Image Features) are popular local descriptors that are also evaluated in this paper. LPQ has been shown to be a significant descriptor used to deal with uncontrolled conditions [ 12] and its principle is based on the quantization of the Fourier transform phase in local neighborhoods [ 10]. In opposition, the BSIF descriptor is used to efficiently represent the facial images based on the statistical features in local regions. The dimensionality reduction process plays a significant role in the information processing area, especially in the biometric systems. Wide different approaches have been proposed in the literature. Principal Component Analysis (PCA) [ 13] and Linear Discriminant Analysis (LDA) [ 14] are two well-known methods [ 15]. They are considered to be basic methods, whose aim is to project the training facial images into a low dimensional space where the recognition of these faces is performed. Most subspace approaches, such as Enhanced Fisher linear discriminant Model (EFM) [ 16], Neighborhood Preserving Embedding (NPE) [ 17], Locality Preserving Projections (LPP) [ 18], and Orthogonal Locality Preserving Projection (OLPP) [ 19], are based on the same principles as PCA and LDA.
1.1 Overview of the Proposed Approach
In this study, local features are used to improve the performance of a 3D face verification system based on 3D depth images. First, the facial region is detected and preprocessed. Then, the facial image is passed through one of the local descriptors and divided into rectangular blocks. After that, the histogram of each block is extracted and concatenated into a single feature vector, which is characterized by a high dimensionality. In order to reduce the dimensionality of these vectors, different methods, namely, PCA, OLPP, and the combined method PCA+EFM, are used. Finally, the multi-class SVM is adopted for classification and verification.
Our proposed approach falls into two steps: the training phase and the test phase. We used the CASIA-3D face database, which contains 123 persons with different variations of illumination, expressions, and combined illumination with expressions. The subjects (persons) were trained as customers and imposters according to a specific protocol during the training phase. The same processing was carried out in the two phases in order to obtain the feature vectors. In the test set, the feature vectors were matched with each sample of the training set using the multi-class SVM to accept the test person as a customer or to reject him as an impostor. The flowchart of the proposed approach is shown in Fig. 1. For more accuracy, the facial area should be located and detected. The nose tip point is used to locate the facial area. The depth image is generated from a 3D point cloud set (x, y, z). Where, each pixel in the x–y plan stores the depth value z. In most cases, the nose tip point has the largest depth value because the nose region is the surface closest to the camera in frontal poses.
To find the nose tip coordinates, the sum of a 3×3 pixel window is calculated. Then, the window, which gives the maximum depth value, indicates the nose area and the nose tip point is the central pixel of this window. Finally, an elliptical mask is centered on the nose tip point to crop the facial area.
Our preprocessing could be achieved using a simple scheme. On the one hand, the noise is removed from the depth images using a median filter, which is an effective tool for noise suppression [ 20]. On the other hand, linear interpolation of the neighboring pixels is used to fill holes that are usually present in the depth images. Fig. 2 shows an example of the proposed detection and preprocessing scheme.
1.2 Contributions of This Paper
In our previous work [ 21, 22] three local descriptors, TPLBP, FPLBP and LPQ are studied. We used only one method, PCA+EFM, with the three local descriptors in order to reduce the dimensionality of the feature vectors. As an extension of the our method proposed in [ 21], we further improve our work on two aspects. On the one hand, we evaluate the important role of dimensionality reduction in the face verification system and compare three methods, PCA, OLPP and PCA+EFM. On the other hand, we have tested a recent and efficient local descriptor named BSIF. Furthermore, we provided a more detailed analysis of these algorithms and compare their performance. The main contributions of this paper can be summarized as follows:
Evaluation of a novel 3D face verification system based on different recent local descriptors, LBP, TPLBP, FPLBP, BSIF, and LPQ. We give a detailed analysis of these algorithms and compared their performances to build an efficient, automatic 3D face verification system in which we can resolve challenges where the expressions and illumination conditions in the training and testing data are very different. Combination of the LPQ descriptor with different face descriptors at the feature level by concatenating the histograms features. Histogram feature extraction-based local features achieved a high verification performance. Assessment and comparison of 3D reduction techniques, PCA (only), OLPP, and PCA+EFM.
2. Related Work
This section highlights the works related to image representation based on local descriptors, as well as the popular methods of dimensionality reduction and their use in face recognition systems.
Choi et al. [ 23] explored 3D shape information to develop an automatic face recognition system based on histogram features. PCA and curvature calculations were used to determinate the symmetry axis of the faces. A facial image is subdivided into several horizontal stripes in order to exploit more information about the local geometry. Then, features are extracted from the depth value in each stripe, where the feature vector corresponds to the histogram of each stripe. To resolve the problem of high frequency illumination and low frequency face features Liu et al. [ 24] proposed another method based on Local Histogram Specification (LHS). This is where a high-pass filter is applied to eliminate the low frequency illumination, and after that, the local histograms and local histograms’ statistics are exploited from natural illumination facial images. The combination of face descriptors (LBP, Gabor, MBC-O) is used in order to improve the results, as well as the fusion of feature extraction methods KLDA and BLDA. Recently, several dimensionality reduction methods have been proposed. In one of them, the OLPP algorithm, which was proposed by Cai et al. [ 19], a new framework for face recognition is developed based on OLPP and the authors proved that OLPP exhibits more discriminative power than Laplacianfaces (LPP). However, only 2D (Yale, ORL, and PIE) face databases were used in the experimental evaluation. In the same context, Wang et al. [ 23] added the Gabor wavelet to OLPP in order to improve the performance of facial expression recognition. After the extraction of Gabor features, OLPP is used to reduce the dimensionality of these features, which are classified using SVM. Their experiments were implemented on ORL and Yale databases, the authors in this work proved that Gabor-OLLP surpassed PCA, LDA, and LPP. Among the excellent descriptors for the facial images appearance, LBP, LPQ, and their extended methods have been widely used in face recognition. TPLBP and FPLBP are new patch-based descriptors proposed by Wolf et al. [ 10]. These authors compared the performance of similarity learning methods to descriptor-based methods in multi-option face identification. These descriptors are based on patch statistics, and their aim is to improve the performance of the LBP descriptor. Ahonen et al. [ 12] worked on the recognition of blurred faces where the LPQ histogram is calculated in local regions. The authors proved that the LPQ descriptor is highly tolerant against the blurring. Almost in the same vein, a multiscale LPQ (MLPQ) was proposed by Chan et al. [ 7] where a multiscale blur-face descriptor based on MLPQ histograms is projected onto the LDA space in order to increase the performance. MLPQ is calculated on small regions in the facial image and these features are combined using Kernel Discriminant Analysis (KDA) fusion. Whereas, Yuan et al. [ 26] exploited both LPQ and LBP in order to obtain the most important features where the feature vectors of LBP and LPQ are concatenated. This work proves that LPQ+LBP provide better results than using each method independently. Furthermore, among the most commonly used local descriptors of the Scale Invariant Feature Transform (SIFT), Soyel and Demirel [ 27] developed a fully automatic facial expression recognition system using facial image representation based on discriminative SIFT (D-SIFT), which is invariant to illumination variations. The Keypoint descriptors of SIFT are used to build a distinctive features. The authors in this work prove the effectiveness of the D-SIFT descriptor compared with Gabor wavelets and LBP to represent the facial features with high discriminative power. BSIF is another recent and excellent descriptor proposed by Kannala and Rahtu [ 28] used for face recognition and texture classification. BSIF exploits the statistical image features based on the automatic learning of a fixed set of filters using a small set of natural images to construct a binary code and efficiently represents the input images. In order to enhance accuracy, the histograms of pixels’ binary codes in local regions are used.
3. Local Descriptor
3.1 Local Phase Quantization
Ojansivu and Heikkilä [ 29] first proposed the LPQ descriptor for use in the texture descriptor and blur texture classification. The LPQ operator is insensitive to centrally symmetric blur, which includes motion [ 29]. Inspired by this idea, we propose the LPQ descriptor as an efficient method to resolve the problem of expression variations in the face verification system, which includes movement in different regions in the facial images that are caused by different facial expressions such as laughing, smiling, anger, surprise, etc. We designed this study to compare LPQ with other recent efficient descriptors. The extraction of local phase information is used by applying the 2D Short-Term Fourier Transform (STFT) calculated above the MxM neighborhood at each pixel x position of the facial image f(x), which is defined by:
The Fourier transform in (1) is evaluated for all positions in the face image using a 1-D convolution for the rows and columns successively. Then, four local Fourier coefficients are calculated where: u1 = [ a, 0] T, u2 = [0, a] T, u3 = [ a, a] T and u4 = [ a, − a] T where a represents the sufficiently highest scalar frequency for which Hui>0 for each pixel position in the depth image, these results in a vector
FXc where: A simple scalar quantizer is used to record the phase information in the Fourier coefficients by observing the sings of real (Re) and imaginary (Im) parts of Fx. The scalar quantizer is given by the following equation:
Where gj(x) is the jth component of the vector Gx = [Re{Fx}, Im{Fx}]. The obtained eight binary coefficients qj(x) are represented as integer values between 0 and 255 using a simple binary coding to get the LPQ labels, FLPQ defined by:
The input depth image is labeled with the LPQ operator and divided into rectangular blocks of equal size.
3.2 Binarized Statistical Image Features
The BSIF descriptor aims at obtaining a statistically significant image representation. The binary code of the input image is computed for each pixel using its response on a fixed set of the filter that are automatically learned based on a statistical properties of a small set of natural images.
Independent Component Analysis (ICA) algorithm is used to train the set of linear filters by maximizing the statistical independence of the filter responses [ 28, 30]. First, the pixels’ BSIF code values are obtained and then their histograms are used to efficiently represent the facial image. As mentioned above, the facial depth image is subdivided into rectangular blocks. Suppose that X is the input image and Wi is a linear filter of size l×l, the filter response si is given by the following equation: Where w and x include the pixels of Wi and X respectively. The binarized feature bi is calculated as follows:
3.2 Local Binary Patterns
The LBP operator was originally proposed by Ojala et al. [ 31] in order to express the texture of image patches. LBP has been widely applied with various algorithms of face recognition systems as a local feature extraction method [ 26]. The LBP description of a pixel image is produced by thresholding the 3×3 neighborhood with the central pixel and devolving the result as a binary code. The process is illustrated in Fig. 3. The LBP operator has been extended to use different neighborhoods sizes by allowing different sampling points and larger neighborhood radii r [ 30]. The values of the sampled points P on the edge of this circle are taken and compared with the value of the central pixel. Given a pixel I with the coordinate (xc, yc), the LBP code can be defined as a decimal form as follows:
Where:
Ic: is the depth values of the central pixel and Ip(1,..,p) are the values of its neighborhood with a radius r. s(x): is a function defined as:
The LBP descriptor is invariant to a uniform global change of illumination because the LBP code of a pixel depends only on the differences between the value of this pixel and its neighborhood.
3.3 Three-Patch Local Binary Patterns
The TPLBP is an extended method of LBP, TPLBP is produced by comparing the values of three patches to produce a single bit value in the code assigned to each pixel, The w×w patches are uniformly located on the circle (ring) of radius r centered at the site of pixel S. The TPLBP operator is given by the following equation:
where d is the distance measure between patches, P is the patch, and f is a threshold function that is calculated as follows:
τ is the threshold of comparison. The principle of the TPLBP operator method is illustrated in Fig. 4.
3.4 Four-Patch Local Binary Patterns
FPLBP is another variation of LBP, and is almost the same as TPLBP. However, there is a difference in the number of rings. In FPLBP two rings with radius r1 and r2 are used and centered in the pixel. The w×w patches distributed around these two rings and the comparison occurs between two center symmetric patches in the inner ring with two center symmetric patches in the outer ring positioned patches away along the circle [ 10]. After the comparison, one bit in each pixel is taken into accounts according to which of the two patches are the most similar. Along each circle, is the center’s symmetric pairs and this value is the final binary code. The FPLBP operator is given by: The principle of the FPLBP method is illustrated in Fig. 5. In our work, we used 8-bit coding for all descriptors (LBP, TPLBP, FPLBP, BSIF, and LPQ). The size of the result feature vector was 256 elements multiplied by the number of blocks of each image. Therefore, a vector with a large size was produced to represent the facial image.
4. Histogram Feature Extraction
As shown in Fig. 6, local descriptors (LBP, TPLBP, FPLBP, BSIF or LPQ) are applied. Then, the facial image is subdivided into rectangular blocks in which the histogram of each block is obtained. Then, all the histograms are concatenated into a one feature vector. Therefore, the histograms are used as discriminative features to represent the local information of the facial image. The histogram represents the information about microstructures, such as edges, spots, and flat areas, in the local regions [ 34]. The histogram ( h) of the input image ( I) is computed as follows:
P is the number of bits.
A high dimensionality of the feature vectors leads to high computational complexity and redundant information. Therefore, we end up with less accurate classification. To avoid this problem, dimensionality reduction is performed.
5. Dimensionality Reduction
5.1 PCA+EFM
PCA is one of the most successful algorithms that has been largely used in the area of image processing and pattern recognition. PCA reduces the high dimensional data to a small significant data. In this paper, in the first experiment we only used the PCA algorithm. Then, we used the PCA followed by an extended algorithm of LDA, which is called EFM, in order to obtain a low dimensional feature vector and to increase the discrimination power in the feature space. An algorithm that summarizes PCA+EFM is presented below. The input image (one class) is represented by one vector after the concatenation of all the histograms. Consider a matrix A= [ A1A2… AM], with N rows and M columns. M is the number of training images and N is the size of the feature vector. Each class or each person is represented by a number of column vectors (samples) with a different variation of illuminations and expressions according to the protocol depicted in Table 1. First, the PCA algorithm is used and we find the linear transformation matrix UPCA of every feature vector in the eigenvectors subspace, where W is the training face vector projection on the eigenvector subspace. The steps to compute the UPCA can be summarized as follows:
Step 1: Find the mean face vector Ā where Ai(i=1,2, …, M) represents the ith column of A.
Step 2: Subtract the mean face Ā from each training face.
Step 3: Calculate the covariance matrix C form the new matrix X, where X = [Q1, Q2, … QM]
-
Step 4: Calculate the eigenvalues V and the eigenvectors U of C. Sort the eigenvectors in decreasing order. The UPCA matrix contains the first k eigenvectors corresponding to the k greatest eigenvalues.
We then find a global linear transformation matrix UPCA of every feature vector in the eigenvectors subspace, in the form of:
Second, in order to improve the discrimination power between classes (column vectors), EFM is used after the PCA. The training face vectors projection on the eigenvector subspace of the PCA algorithm (W) is an input for EFM. The EFM algorithm, which is presented below as:
-
Step 5: Find the intra-class (Sw) and inter-class (Sb) dispersion matrices
Where: Wij is the j-th samples of the class i, m̄i is the mean of the samples in the class i, m̄ is the mean of all samples, and ni is the number of samples in the class i.
Step 6: Calculate the eigenvalues (Y) and the eigenvectors vectors (E) of the Sw matrix. Step 7: Calculate the new inter-class matrix Kb:
Step 8: Calculate the eigenvalues (O) and the eigenvectors vectors (H) of Kb. Step 9: Calculate the global transformation matrix UEFM.
Finally, the final training face images projection (Wfinal) on the subspace described by the eigenvector is calculated using the global linear transformation matrix UEFM, in the form of:
The projection of the test images is then compared with each training projection using a multi-class SVM.
5.2 Orthogonal Locality Preserving Projection
OLPP, which is also called orthogonal Laplacianface is an appearance-based face recognition method proposed by Cai et al. [ 19]. OLPP requires the basic functions to be orthogonal and can have more locality preserving and more discriminating power than LPP. Let { x1, x2, …. xk} is a given set in Rl to find a transformation matrix A that projects the k points to a set of points { y1, y2,…. yk} in Rm where m≪l, and yi = AT* xi. The OLPP algorithm includes five steps [ 19], which are described below:
-
Step 1: PCA projection
The facial images xi are projected into the PCA subspace. The PCA matrix transformation is represented by WPCA. The uncorrelated features are extracted and the rank of the new data matrix is equal to the number of features.
-
Step 2: The Adjacency Graph
Let G indicate a graph with k nodes. The ith node corresponds to the facial images xi. An edge is placed between nodes i and j, if xi and xj are close, xi is among the p nearest neighbors of xj or vice versa. The Adjacency Graph is an approximation of the local manifold structure. If the class information is available, we simply put an edge between two data points belonging to the same class.
-
Step 3: Calculate the weights.
Where t is a suitable constant. The weight matrix Wij of graph G models the face manifold structure by preserving the local structure.
-
Step 4: The orthogonal basis functions
Let D denote a diagonal matrix where whose entries are column or row ( W is symmetric) sums of W. Di = ∑ j Wji, the Laplacian matrix is defined by L = D − W. Let { a1, a2, …. ak} be the orthogonal basis vectors and we define:
The orthogonal basis vector {a1, a2, ….ak} is computed as shown below:
– Compute a1, the eigenvector of (XDXT)−1XDX associated with the smallest eigenvalues. – Compute ak, the eigenvector of:
M(k)= {I−(XDXT)−1A(k−1) [B(k−1)]−1 [A(k−1)]T}. (XDXT)−1XDXT is associated with the smallest eigenvalues of M(k).
-
Step 5: OLPP Embedding
Let WOLPP = [ a1, a2, …. al], the embedding is given as follows:
Where y is the l-dimensional representation of the facial image x, and W is the final transformation matrix.
6. Classification Using a Support Vector Machine
After the representation of each face image that has a high discriminative power, classification is conducted as the last step in our system, where the decision is performed between the test face and the training faces in the database. SVM is an efficient statistical learning method widely used to deal with pattern recognition problems. At first, SVM is used as a binary classification method, which is based on a two-class problem. The binary SVM seeks to find the optimal separating hyperplane between the two classes by maximizing the margin between the hyperplane and the two classes, which are labeled −1 and 1. Suppose that A is a dataset, xi are the training feature vectors in k-dimensional and yi are the labels, which is shown as:
In the linear SVM, the optimal separating hyperplane can be expressed as:
The accuracy of the SVM classifier also depends on the kernel function used in [ 35]. In the case of non-linear SVM, the decision function is not linear. As such, the input data is reconstructed to be in a high dimensional space based on a kernel function, in order to increase classification accuracy. The linear and polynomial kernels surpass the RBF (Radial Basis Function) kernel in the application of face recognition [ 35, 36]. After that, the SVM classifier is generalized to solve the multi-class problem. The multi-class SVM algorithms can be divided into the two categories of One-Versus-All and One-Versus-One [ 32, 36]. In our work, we used the One-Versus-All SVM-based RBF kernel to carry out the verification of facial images between imposters and customers. One-Versus-All is a simple method in which we use M classifiers (one for each class). The last classifier is trained to classify the training data of class k versus other training classes. The final decision on the M-class is carried out by the combination of each classifier.
7. Experiments and Results
7.1 Experimental Data
This section provides the details about the experimental results of the proposed system. To demonstrate the effectiveness of our proposed approach, the experiments were performed on the CASIA 3D face database, which contains 123 persons (subjects) with 37 or 38 scans. In this work, we used 1,845 images where each person was represented using 15 different models, which were divided as follows:
The scans (001 to 005) with illumination variations under neutral expression, The scans (006 to 010) with the five expression variations of laughter, smiling, anger, surprise, eyes close as seen under office lighting. The scans (011 to 015) with expressions under illumination variations.
As shown in Table 1, our protocol includes three data partitions: training, evaluation, and testing. The 123 persons were separated into two classes of customers and impostors. The customer class contained 100 subjects, while the impostor class was subdivided into 13 impostors for evaluation and 10 impostors for testing. Fig. 7 shows the 15 scans of depth images of the same person in the CASIA-3D face database.
7.2 Discussion
As previously outlined, in the first experiments, the proposed 3D face verification system was comprehensively evaluated on the different local descriptors of TPLBP, FPLBP, BSIF, and LPQ with three dimensionality reduction methods—PCA, OLPP and PCA+EFM. In the second set of experiments, the combination of LPQ features with all other descriptors was used with the best method of dimensionality reduction. The Equal Error Rate (EER) describes the performance of the proposed system on the evaluation set. EER is the point that corresponds to a value where the False Acceptance Rate (FAR) is equal to the False Rejection Rate (FRR). In the test set, we calculated the Half Total Error Rate (HTER), which is defined as the average of FRR and FAR, the Verification Rate (VR) at 0.01% FAR, and Processing Time (PT). Finally, the Operating Characteristic Curves (ROCs) were plotted.
The experimental results were obtained with the optimal parameters of TPLBP and FPLBP, as shown in Table 2. The LPQ descriptor is based on the quantization of the Fourier transform phase in the local neighborhoods of 3×3 windows at each pixel, and the size of the linear filter used for the BSIF descriptor was 17×17. All of these parameters were chosen experimentally. Fig. 8 illustrates the input depth image and the code image of LPQ, TPLBP, FPLBP, BSIF, and LBP.
Tables 3– 5 show the verification results of PCA, OLPP, and PCA+EFM with the four local descriptors. It can be seen that OLPP and PCA+EFM achieved a considerable improvement of more than 9% to 11% for the verification rate as compared to the basic algorithm PCA. For example, with the FPLBP operator, the verification rates of PCA, OLPP, and PCA+EFM were 86.65%, 93.98%, and 96.68%, respectively. Also, depending on the TPLBP operator we got a verification rate of 83.22%, 92.88%, and 96.48% using PCA, OLPP, and PCA+EFM, respectively. Moreover, the results presented in Tables 3– 5 during the evaluations and tests indicate that LPQ and BSIF-based PCA+EFM can lead to a high verification performance. We obtained a verification rate of 97.26% and 98.18% with BSIF and LPQ, respectively. We can also confirm this result through the ROC curves of different experiments that are illustrated in Figs. 9– 11. The ROC curve plots the verification rate versus the false acceptance rate.
Moreover, we tested the performance of our system with the traditional LBP descriptor. We used the LBP descriptor with the best method of dimensionality reduction, PCA+EFM, in order to compare the results with the extended versions of TPLBP and FPLBP. After several experiences of LBP, the code image with P=16 and r=2 were found to provide the best results.
BSIF had the second best verification performance after LPQ for all of the dimensionality reduction methods, except in one case when we used the basic algorithm, PCA, we got a low verification rate of 85.66%, as depicted in Table 1. The LPQ histograms explore more sufficient discriminant features and outperformed all other features with a verification rate of VR=98.18%. We can say that the LPQ descriptor based on PCA+EFM is one of the best frameworks to address the effects of illumination and expression variation problems in the face verification system. We attribute this to the fact that illumination and expression variations have little or no effect on the frequency domain, which is represented by the LPQ descriptor. Based on these results in the second set of experiments, the combination of LPQ with all descriptors was used. Table 6 presents the verification accuracy of the combination of LPQ with the other descriptor based on PCA+EFM. As can be seen in this table, the verification performance during the test set using LPQ_FPLBP outperformed both LPQ_TPLBP and LPQ_BSIF (VR=98.22%, HTER=0.88%). We can conclude that the histogram combination of the local features-based LPQ_FPLBP method using 3D depth images provides more distinct features using PCA+EFM. This optimal approach produced a significant improvement in the 3D face verification system’s performance.
The results depicted in Tables 5 and 6 show that the extended methods of TPLBP and FPLBP may outperform the traditional LBP descriptor, but there is not a large difference between them. We can see that there is no significant performance gain in the combined methods and that the LPQ descriptor alone outperformed some combined methods, such as LPQ_TPLBP, LPQ_BSIF, and LPQ_LBP. This is due to the fact that these descriptors share a lot of similar features, which leads to the problem of the redundancy of information, thereby resulting in the weakening of the classification process.
All of our experiments were finished in MATLAB R2010b on a PC with 2.53GHz Intel Core i5 CPU and a RAM of 4Go. In Table 5 we present the Processing Time (PT) of each method. There is basically no significant PT between all experiments (1.90(s)–1.13(s)), because all of the proposed methods used almost the same size of feature vectors. As we can observe in Table 6, the combined methods increased the PT because we concatenated two feature vectors when the first was the LPQ descriptor and the second was one of the rest descriptors used in this work (LBP, TPLBP, FPLBP, BSIF). We also examined the effects of the variation of the feature vectors size. We were able to determine the best dimensions of the feature vector experimentally by varying its size between 10 and 100. Fig. 12 illustrates the variation of the verification rate across the dimensions of the feature vector. From this figure we concluded that the optimal discriminant projection vector of the four combined methods (LPQ_LBP, LPQ_FPLBP, LPQ_BSIF, and LPQ_TPLBP) is located between 70 and 90, when using our method of PCA+EFM. Table 7 provides a comparison of our best results in terms of the verification rate with several techniques existing in the literature that used the CASIA 3D database. Our proposed approach achieved a high verification rate of 98.22%.
8. Conclusions
In this paper, automatic 3D face verification in the presence of illumination and expression variations using depth images has been proposed. Five of the most efficient local descriptors LBP, LPQ, BSIF, TPLBP, and FPLBP were performed to provide more discriminative power to the facial images. The histograms of each descriptor were extracted on rectangular blocks and concatenated into a single feature vector. In order to reduce the high dimensionality of the feature vectors, several dimensionality reduction methods, PCA, OLPP, and PCA+EFM were assessed and compared. We have demonstrated that the combined method of LPQ_FPLBP based on PCA+EFM achieves a high verification performance with a verification rate of 98.22% at 0.01% FAR and HTER of 0.88%. We have also stressed the important role of dimensionally reduction. Our experimental results show that the PCA+EFM method achieved more than 10% in the verification rate and 5.8% in the EER compared with the basic method PCA. In the future, we intend to study our system in the presence of large pose variations using tensor analyses.
Biography
He has a master degree in Electronic Telecommunication from University of Mohammed Khider Biskra, Algeria in 2011 at the Department of Electrical Engineering. Currently, he is a Ph.D. student at the same university. His research interests are in: image processing, feature extraction, face detection, tensor analysis; classification, computer vision, biometric techniques and face recognition systems.
Biography
Belahcene Mebarka
She received his Ph.D. degree from University of Mohammed Khider Biskra, Algeria in 2013. Currently, he is a Professor at Electrical Engineering Department at the same university. His research interests are in signal processing, image processing, image compression, classification, biometric techniques and face recognition systems.
Biography
Ouamene Abdelmalik
He is a researcher in CDTA (Centre de développement des technologies avancées) in Algeria. He is received her Ph.D. in 2015 from the University of Mohammed Khider Biskra, Algeria. He is a reviewer & community members in differences conferences and journals. His research interests are in, image processing, classification, image representation and modeling, signal processing, Multimodal biometric authentication and identification systems.
Biography
Bourennane Salah
He received his Ph.D. degree from Institut National Polytechnique de Grenoble, France, in 1990 in signal processing. Currently, he is a full Professor at the Ecole Centrale de Marseille, France. His research interests are in statistical signal processing, array processing, image processing, tensor signal processing, and performances analysis.
References
1. Y. Ming, "Rigid-area orthogonal spectral regression for efficient 3D face recognition," Neurocomputing, vol. 129, pp. 445-457, 2014.  2. Y. Ming, Q. Ruan, and X. Wang, "Efficient 3d face recognition with Gabor patched spectral regression," Computing and Informatics, vol. 31, no. 4, pp. 779-803, 2012.
3. A. Mian, M. Bennamoun, and R. Owens, "Face recognition using 2D and 3D multimodal local features," in Advances in Visual Computing, Heidelberg: Springer, 2006, pp. 860-870.  4. F. Hajati, AA. Raie, and Y. Gao, "2.5 D face recognition using Patch Geodesic Moments," Pattern Recognition, vol. 45, no. 3, pp. 969-982, 2012.  5. C. Xu, S. Li, T. Tan, and L. Quan, "Automatic 3D face recognition from depth and intensity Gabor features," Pattern Recognition, vol. 42, no. 9, pp. 1895-1905, 2009.  6. T. Ahonen, A. Hadid, and M. Pietikäinen, "Face recognition with local binary patterns," in Computer Vision-ECCV 2004, Heidelberg: Springer, 2004, pp. 469-481.  7. CH. Chan, MA. Tahir, J. Kittler, and M. Pietikainen, "Multiscale local phase quantization for robust component-based face recognition using kernel fusion of multiple descriptors," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 35, no. 5, pp. 1164-1177, 2013.  8. CH. Chan, J. Kittler, N. Poh, T. Ahonen, and M. Pietikainen, "(Multiscale) Local phase quantisation histogram discriminant analysis with score normalisation for robust face recognition," in Proceedings of IEEE 12th International Conference on Computer Vision Workshops (ICCV Workshops), Kyoto, Japan, pp. 633-640.  9. Z. Lei, T. Ahonen, M. Pietikäinen, and SZ. Li, "Local frequency descriptor for low-resolution face recognition," in Proceedings of IEEE International Conference on Automatic Face & Gesture Recognition and Workshops (FG 2011), Santa Barbara, CA, pp. 161-166.  10. L. Wolf, T. Hassner, and Y. Taigman, "Descriptor based methods in the wild," in Workshop on Faces in ‘Real-Life’ Images: Detection, Alignment, and Recognition, Marseille, France: 2008.
11. D. Huang, C. Shan, M. Ardabilian, Y. Wang, and L. Chen, "Local binary patterns and its application to facial image analysis: a survey," IEEE Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews, vol. 41, no. 6, pp. 765-781, 2011.  12. T. Ahonen, E. Rahtu, V. Ojansivu, and J. Heikkilä, "Recognition of blurred faces using local phase quantization," in Proceedings of 19th International Conference on Pattern Recognition (ICPR 2008), Tampa, FL, 2008, pp. 1-4.  13. M. Turk, and AP. Pentland, "Face recognition using eigenfaces," in Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’91), Maui, HI, 1991, pp. 586-591.  14. PN. Belhumeur, JP. Hespanha, and DJ. Kriegman, "Eigenfaces vs. fisherfaces: recognition using class specific linear projection," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 19, no. 7, pp. 711-720, 1997.  15. M. Safayani, and MTM. Shalmani, "Three-dimensional modular discriminant analysis (3DMDA): a new feature extraction approach for face recognition," Computers & Electrical Engineering, vol. 37, no. 5, pp. 811-823, 2011.  16. C. Liu, and H. Wechsler, "Gabor feature based classification using the enhanced fisher linear discriminant model for face recognition," IEEE Transactions on Image processing, vol. 11, no. 4, pp. 467-476, 2002.  17. X. He, D. Cai, S. Yan, and HJ. Zhang, "Neighborhood preserving embedding," in Proceedings of 10th IEEE International Conference on Computer Vision (ICCV2005), Beijing, China, 2005, pp. 1208-1213.
18. X. He, S. Yan, Y. Hu, P. Niyogi, and HJ. Zhang, "Face recognition using Laplacianfaces," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 27, no. 3, pp. 328-340, 2005.  19. D. Cai, X. He, J. Han, and HJ. Zhang, "Orthogonal Laplacianfaces for face recognition," IEEE Transactions on Image Processing, vol. 15, no. 11, pp. 3608-3614, 2006.  20. A. Chouchane, M. Belahcene, A. Ouamane, and S. Bourennane, "3D face recognition based on histograms of local descriptors," in Proceedings of 4th International Conference on Image Processing Theory, Tools and Applications (IPTA), Paris, France, 2014, pp. 1-5.  21. A. Chouchane, M. Belahcene, A. Ouamane, and S. Bourennane, "Multimodal face recognition based on histograms of three local descriptors using score level fusion," in Proceedings of 2014 5th European Workshop on Visual Information Processing (EUVIP), Paris, France, 2014, pp. 1-6.  22. P. Bagchi, D. Bhattacharjee, M. Nasipuri, and DK. Basu, "A novel approach for nose tip detection using smoothing by weighted median filtering applied to 3D face images in variant poses," in Proceedings of 2012 International Conference on Pattern Recognition, Informatics and Medical Engineering (PRIME), Salem, India, 2012, pp. 272-277.  23. X. Zhou, H. Seibert, C. Busch, and W. Funk, "A 3d face recognition algorithm using histogram-based features," in Proceedings of the 1st Eurographics conference on 3D Object Retrieval, Crete, Greece, 2008, pp. 65-71.
24. HD. Liu, M. Yang, Y. Gao, and C. Cui, "Local histogram specification for face recognition under varying lighting conditions," Image and Vision Computing, vol. 32, no. 5, pp. 335-347, 2014.  25. L. Wang, R. Li, K. Wang, and C. Cao, "OLPP-based Gabor feature dimensionality reduction for facial expression recognition," in Proceedings of 2014 IEEE International Conference on Information and Automation (ICIA), Hailar, China, 2014, pp. 455-460.  26. B. Yuan, H. Cao, and J. Chu, "Combining local binary pattern and local phase quantization for face recognition," in Proceedings of 2012 International Symposium on Biometrics and Security Technologies (ISBAST), Taipei, Taiwan, 2012, pp. 51-53.  27. H. Soyel, and H. Demirel, "Localized discriminative scale invariant feature transform based facial expression recognition," Computers & Electrical Engineering, vol. 38, no. 5, pp. 1299-1309, 2012.  28. J. Kannala, and E. Rahtu, "BSIF: binarized statistical image features," in Proceedings of 21st International Conference on Pattern Recognition (ICPR), Tsukuba, Japan, 2012, pp. 1363-1366.
29. V. Ojansivu, and J. Heikkilä, "Blur insensitive texture classification using local phase quantization," in Image and Signal Processing, Heidelberg: Springer, 2008, pp. 236-243.  30. A. Hadid, J. Ylioinas, and MB. Lopez, "Face and texture analysis using local descriptors: a comparative analysis," in Proceedings of 2014 4th International Conference on Image Processing Theory, Tools and Applications (IPTA), Paris, France, 2014, pp. 1-4.  31. T. Ojala, M. Pietikainen, and T. Maenpaa, "Multiresolution gray-scale and rotation invariant texture classification with local binary patterns," IEEE Transactions on Pattern Anal, vol. 24, no. 7, pp. 971-987, 2002.  32. L. Zhao, Y. Song, Y. Zhu, C. Zhang, and Y. Zheng, "Face recognition based on multi-class SVM," in Proceedings of Chinese Control and Decision Conference (CCDC’09), Guilin, China, 2009, pp. 5871-5873.
33. M. Roschani, "Evaluation of local descriptors on the labeled faces in the wild dataset,"Ph.D. dissertation, Institute for Anthropometrics, University of Karlsruhe; German: 2009.
34. S. Meshgini, A. Aghagolzadeh, and H. Seyedarabi, "Face recognition using Gabor-based direct linear discriminant analysis and support vector machine," Computers & Electrical Engineering, vol. 39, no. 3, pp. 727-745, 2013.  35. Y. Lei, M. Bennamoun, and AA. El-Sallam, "An efficient 3D face recognition approach based on the fusion of novel local low-level features," Pattern Recognition, vol. 46, no. 1, pp. 24-37, 2013.  36. CW. Hsu, and CJ. Lin, "A comparison of methods for multiclass support vector machines," IEEE Transactions on Neural Networks, vol. 13, no. 2, pp. 415-425, 2002.
37. X. Wang, Q. Ruan, and Y. Ming, "3D face recognition using corresponding point direction measure and depth local features," in Proceedings of 2010 IEEE 10th International Conference on Signal Processing (ICSP), Beijing, China, pp. 86-89.  38. YA. Li, YJ. Shen, GD. Zhang, T. Yuan, XJ. Xiao, and HL. Xu, "An efficient 3D face recognition method using geometric features," in Proceedings of 2010 2nd International Workshop on Intelligent Systems and Applications (ISA), Wuhan, China, pp. 1-4.  39. A. Ouamane, M. Belahcene, A. Benakcha, S. Bourennane, and A. Taleb-Ahmed, "Robust multimodal 2D and 3D face authentication using local feature fusion," Signal, Image and Video Processing; pp. 1-9, 2014, http://dx.doi/org/10.1007/s11760-014-0712-x. 
Fig. 1
The flowchart of the proposed 3D faces verification system. 
Fig. 2
Detection and preprocessing of the 3D depth image. (a) Input depth image, (b) detection, (c) pre-processing. 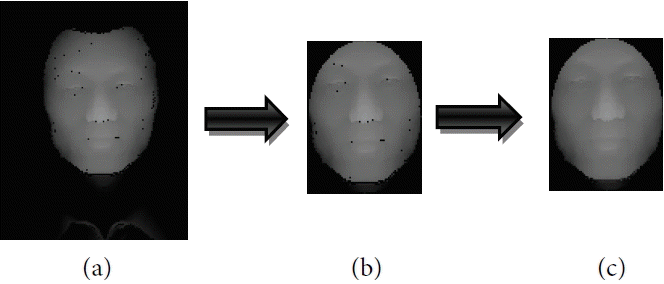
Fig. 3
Example of the LBP operator. 
Fig. 4
The three-patch LBP representations. 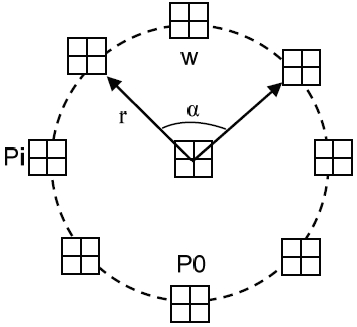
Fig. 5
The four-patch LBP representations. 
Fig. 6
Descriptors and histograms feature extraction. 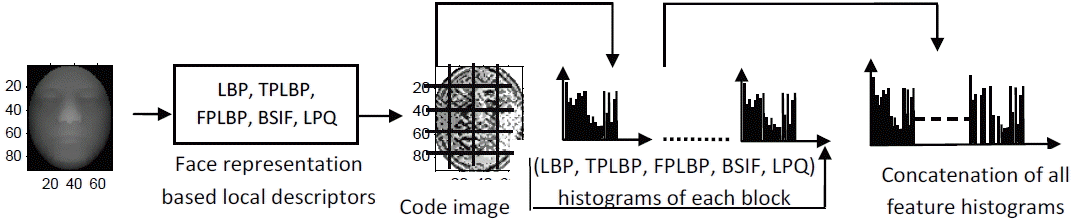
Fig. 7
Sample images of the same person in the CASIA 3D database. 
Fig. 8
Facial representation based Local descriptors. (a) Original depth image detected and preprocessed, (b) LPQ code image, (c) TPLBP code image, (d) FPLBP code image, (e) BSIF code image; (f) LBP code image. 
Fig. 9
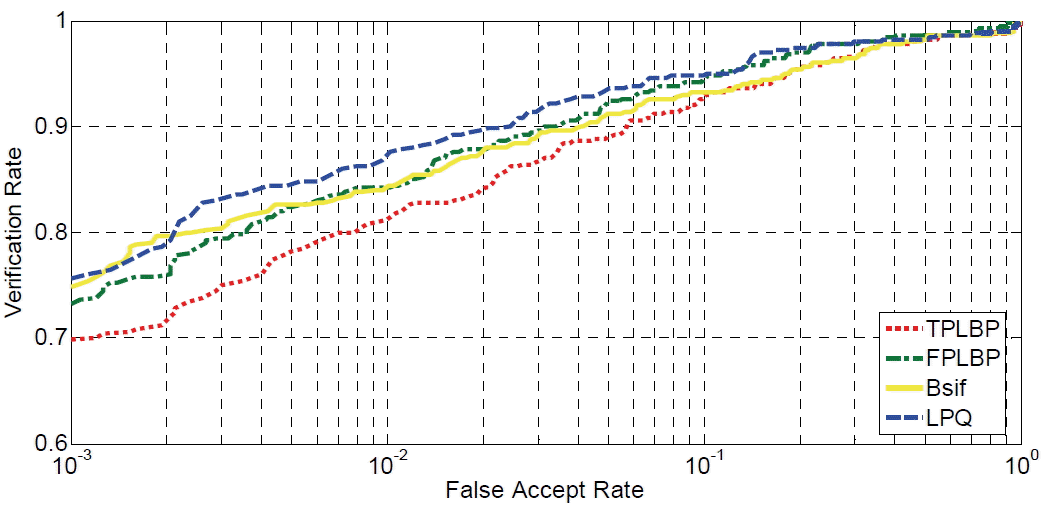
Fig. 10
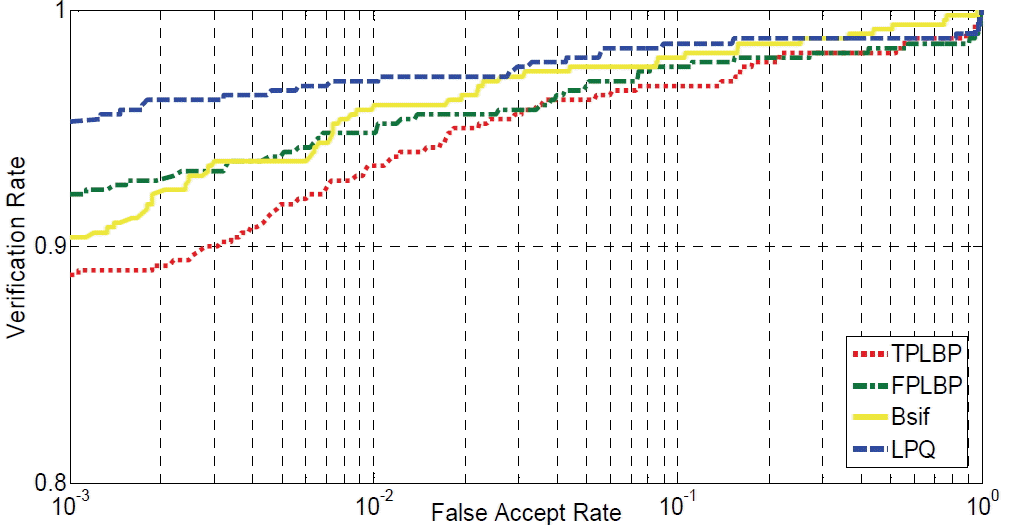
Fig. 11
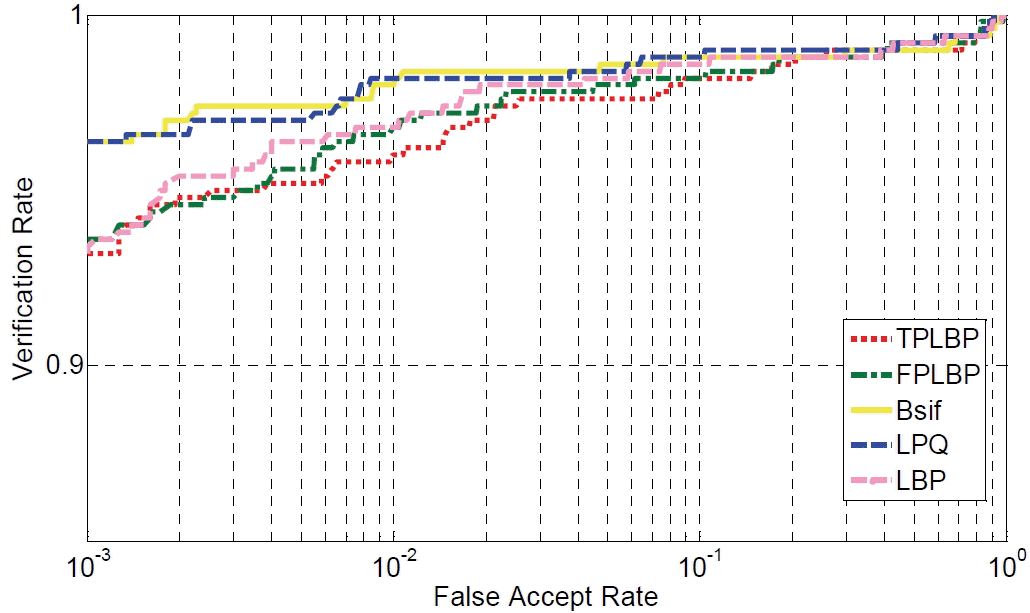
Fig. 12
Variation of verification rate across the dimension of the feature vector. 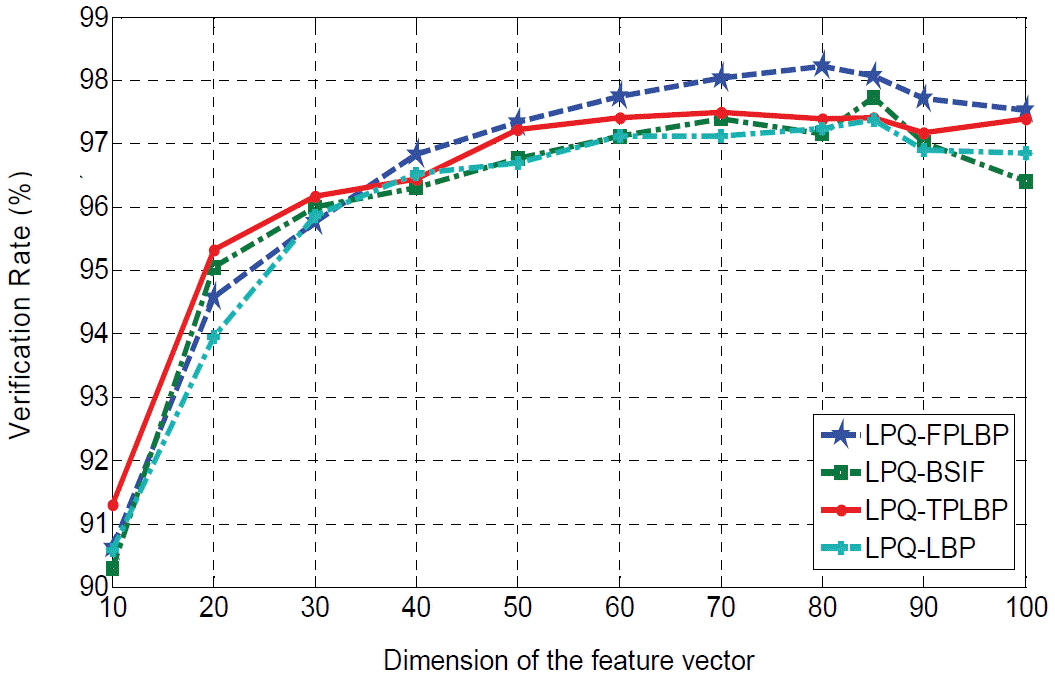
Table 1
Protocol used for verification process
|
Dataset |
Customer |
Imposter |
|
Training |
500 images (1, 4, 8, 9, 10) |
0 image |
|
Evaluation |
500 images (2, 6, 7, 14, 15) |
195 images (1:15) |
|
Test |
500 images (3, 5, 11, 12, 13) |
150 images (1:15) |
Table 2
Optimal parameters of TPLBP and FPLBP
|
Operator |
r1 |
r2 |
S
|
w
|
τ
|
|
TPLBP
|
3 |
/ |
8 |
5 |
0.01 |
|
FPLBP
|
1 |
5 |
12 |
5 |
0.01 |
Table 3
Verification accuracy with PCA during test and evaluation
|
Local descriptor |
Evaluation |
Test |
|
EER (%) |
HTER (%) |
VR (%) |
|
TPLBP |
10.77 |
8.39 |
83.22 |
|
FPLBP |
8.74 |
6.67 |
86.65 |
|
BSIF |
8.79 |
7.15 |
85.66 |
|
LPQ |
7.04 |
6.62 |
87.46 |
Table 4
Verification accuracy with OLPP during test and evaluation
|
Local descriptor |
Evaluation |
Test |
|
EER (%) |
HTER (%) |
VR (%) |
|
TPLBP |
5.15 |
3.56 |
92.88 |
|
FPLBP |
4.78 |
3.01 |
93.98 |
|
BSIF |
3.60 |
2.90 |
94.19 |
|
LPQ |
2.35 |
1.98 |
96.02 |
Table 5
Verification accuracy with PCA+EFM during test and evaluation
|
Local descriptor |
Evaluation |
Test |
|
EER (%) |
HTER (%) |
VR (%) |
PT (%) |
|
LBP |
3.03 |
1.96 |
96.08 |
1.27 |
|
TPLBP |
1.90 |
1.75 |
96.48 |
1.13 |
|
FPLBP |
1.90 |
1.65 |
96.68 |
1.91 |
|
BSIF |
2.42 |
1.37 |
97.26 |
1.18 |
|
LPQ |
1.20 |
0.90 |
98.18 |
1.48 |
Table 6
Verification accuracy based PCA+EFM on combining LPQ with TPLBP, FPLBP and BSIF
|
Local descriptor |
Evaluation |
Test |
|
EER (%) |
HTER (%) |
VR (%) |
PT (%) |
|
LPQ_LBP |
1.60 |
1.31 |
97.37 |
2.40 |
|
LPQ_TPLBP |
1.80 |
1.25 |
97.49 |
2.80 |
|
LPQ_BSIF |
1.40 |
1.13 |
97.73 |
3.03 |
|
LPQ_FPLBP |
1.30 |
0.88 |
98.22 |
2.99 |
Table 7
Comparison of verification rate with state-of-art
|
Author |
Method |
Database |
VR (%) |
|
Wang et al. [37] 2010 |
ICP, PCA, Gabor filter, LBP, Corresponding Point Direction Measure (CPDM) |
CASIA 3D |
91.71 |
|
Li et al. [38] 2010 |
Geometric feature, ICP, LDA, geodesic distance |
CASIA3D |
91.10 |
|
Ming [1] 2013 |
Orthogonal Spectral Regression (OSR), PCA Curvature, Distance Metric, ICP, Nearest Neighbor Classifier |
CASIA3D |
96.25 |
|
Ming et al. [2] 2012 |
Gabor features, patched spectral regression, LDA |
CASIA 3D |
96.35 |
|
Ouamane et al. [39] 2014 |
LBP, SIFT, SLF, SVM |
CASIA 3D |
96.26 |
|
Our method |
LPQ_FPLBP, PCA+EFM, SVM |
CASIA 3D |
98.22 |
|















