Counter Chain: A New Block Cipher Mode of Operation
Article information
Abstract
In this paper, we propose a novel block cipher mode of operation, which is known as the counter chain (CC) mode. The proposed CC mode integrates the cipher block chaining (CBC) block cipher mode of operation with the counter (CTR) mode in a consistent fashion. In the CC mode, the confidentiality and authenticity of data are assured by the CBC mode, while speed is achieved through the CTR mode. The proposed mode of operation overcomes the parallelization deficiency of the CBC mode and the chaining dependency of the counter mode. Experimental results indicate that the proposed CC mode achieves the encryption speed of the CTR mode, which is exceptionally faster than the encryption speed of the CBC mode. Moreover, our proposed CC mode provides better security over the CBC mode. In summary, the proposed CC block cipher mode of operation takes the advantages of both the Counter mode and the CBC mode, while avoiding their shortcomings.
1. Introduction
In recent years, many block cipher modes of operation have been proposed. A mode of operation is a way of encrypting long plain text files with a block cipher. Based on the recommendation [1] of the National Institute of Standards and Technology (NIST), there are five main block cipher modes of operation: the electronic code book (ECB), cipher block chaining (CBC), cipher feedback (CFB), the output feedback mode (OFB), and the counter (CTR) mode. In the ECB [2], under a given key, encrypting the same plaintext results in the same ciphertext. This is practically undesirable in critical applications. Therefore, ECB is not widely used. With CBC [3], chaining of the plaintext blocks with the previous ciphertext blocks is proposed. The CBC mode requires an initial vector (IV) to be combined with the first plaintext block. The IV need not be secret. However, it must be unpredictable. The CFB [4] permits the encryption of differing block sizes by feeding the successive ciphertext blocks into the input blocks of the forward cipher to generate output blocks that are exclusive-ORed with the plaintext to produce the ciphertext. However, the CFB suffers from the error propagation problem in which errors in the incoming cipher block will lead to errors in the plain text block.
In the OFB mode [5], the output of the encryption block is the feedback (instead of the ciphertext). The exclusive-OR value of each plaintext block is created independently of both the plaintext and ciphertext. The CTR mode [1] provides parallel encryption through encrypting a non-repeating sequence of blocks with the block cipher and the output is exclusive-ORed to the plaintext blocks in order to create the ciphertext blocks.
In addition to the five main block cipher modes, other hybrid modes of operation have been proposed. The CTR mode with the CBC-MAC mode (CCM) [6] integrates the CBC-MAC mode with CTR authentication and the CTR mode for achieving data encryption. EAX [7] uses the CTR mode for data encryption and the OMAC [8] hash algorithm for data authentication. The OMAC algorithm is based on the CBC-MAC hashing approach, but it uses an additional padding method. The Galois/Counter Mode (GCM) [9] provides authenticated encryptions at a high speed by using binary field multiplication to provide authentication. In terms of implementation costs, GCM can be implemented at a fraction of the cost of the CTR mode at high speeds. CYPHER-C3 [10] is a combined block cipher mode of operation that provides an efficient authenticated encryption with associated data (AEAD) security service for packet-based network communication. CYPHER-C3 achieves improved performance in processing, energy requirements, processing latency, and packet throughput when compared to CCM. The pipelined statistical cipher feedback (PSCFB) mode [11] is an enhancement to the conventional statistical cipher feedback (SCFB) [12]. PSCFB uses pipeline architectures for the block cipher, which makes it suitable for high-speed network applications requiring stream-oriented encryption with self-synchronizing capabilities.
In this paper we propose a simple and efficient block cipher mode of operation that is similar to the CCM mode, which combines the CBC mode with the CTR mode. However, our proposed counter chain (CC) mode, uniquely achieves a very high encryption speed through parallelizable architecture. The proposed mode overcomes the main drawback of the CBC mode, which is the fact that encryption is sequential, by making use of the fact that the CTR mode is well suited to operate on a multi-processor machine where messages can be encrypted in parallel.
The remainder of this paper is organized as follows: in the next section, related work is presented. We describe our CC mode of operation in Section 3, while Section 4 provides an interesting discussion comparing our CC mode with other block cipher modes of operation. In Section 5, we present some experimental results of our proposed mode of operation. Finally, the paper is concluded in Section 6.
2. Related Work
In this section we focus on block cipher modes of operation that are related to our proposed CC mode. In particular, we will discuss the merits and demerits of each of the following modes: the CBC mode, the CTR mode, and the CCM mode.
2.1 CBC Mode of Operation
In CBC, plaintext is divided into blocks of m bytes based on the block size of the encryption algorithm. For example, if the DES or AES128 algorithm is used, m will be 8 or 16, respectively. Then, the data blocks are chained together. Here, the ciphertext has a fixed size to eliminate the risk of including the message size in the message itself, which can be useful to an attacker. Therefore, the final data block must be padded if the size of the last block is less than the block size. The CBC mode uses an IV to provide chain dependency between ciphertext blocks (i.e., block n depends on block n–1, which in turn depends on block n–2, and so on, until the first block that is dependent on the IV is reached. Since the CBC mode uses the IV with all messages, it will produce the same ciphertext for the same message encrypted with the same encryption key and IV. This shortcoming is addressed in the design of the CC mode by changing the IV for each message. As a result, the produced ciphertext will be different each time, even if the same message is encrypted again. This improves the security of the CC over the CBC. Another drawback of the CBC mode is error propagation. This error propagation range in CBC is one block. This means that one bit error in a ciphertext block affects the corresponding plaintext block, as well as the following block.
2.2. CTR Mode of Operation
In the CTR mode, a counter that starts from the preconfigured initial value together with a nonce that is similar to the initial vector is used to generate a key stream. The key stream is exclusive-ORed into the plaintext to produce the ciphertext.
The advantages of the CTR mode are tremendous and one of these advantages involves being able to overcome the error propagation problem of the CBC mode. The CTR mode does not require that the plaintext be padded to the block size of the cipher. Moreover, in the CTR mode, the encryption of a plaintext block does not depend on the result from previous blocks. Therefore, the CTR mode of operation has become the mode of choice for high-speed applications [13] due to its highly parallelizable architecture. On the other hand, the CTR mode encryption provides no message integrity.
2.3 CCM Mode of Operation
The CCM mode is a two-pass authenticated encryption scheme (AES) of operation that uses a single key and that integrates the CBC-MAC mode with the CTR mode to produce an authenticated encryption scheme. It uses CBC-MAC for providing data authentication and the CTR mode for achieving data encryption. Although it is efficient in providing an authenticated encryption, it has several drawbacks that were indicated in [7] and are listed below.
▪ CCM is only defined for use with 128-bit block ciphers, such as AES.
▪ CCM is not suited to high-speed implementations because CBC-MAC is neither pipelinable nor parallelizable.
▪ Typically, CCM is double the computational cost of the one-pass AES.
▪ CCM is not an online scheme (i.e., it needs to know the lengths of both the plaintext and the associated data before one can proceed with encryption). Hence, CCM does not allow for the preprocessing of static associated data.
▪ CCM uses a nonce, which means that its length is restricted in such a way that it may not provide adequate security when a nonce is randomly chosen.
▪ Finally, CCM implementations could suffer performance hits because the associated algorithm can disrupt word alignment in the associated data.
3. Proposed Counter Chain Mode of Operation
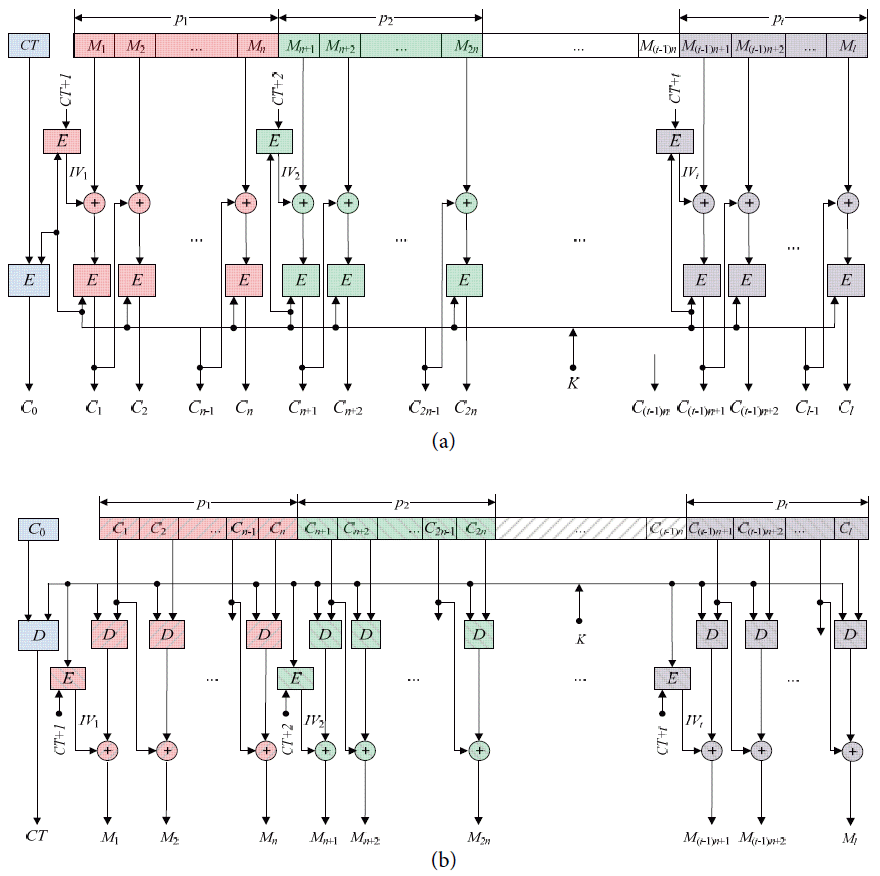
To overcome the parallelization deficiency of the CBC mode and the chaining dependency shortcoming of the CTR mode, we propose a new mode of operation called the CC mode. The CC mode takes the advantages of both modes and overcomes their shortcomings. Therefore, the CC mode provides both chaining dependency and improves efficiency, as well as producing different ciphertext blocks for repeated or same plaintext blocks. The encryption and decryption in the CC mode is depicted in more details in Fig. 1(a) and (b), respectively.
In the CC mode, the plaintext M is divided into a sequence of l blocks: M = M1M2…Ml such that the length of each block Mi is equal to the block size of the block cipher encryption algorithm that will be used for encryption, where i = 1, 2, …, l and Ml is padded if required. For example, the length of Mi denoted by |Mi| is 64 or 128 when using DES or AES encryption algorithms [14], respectively. To provide parallelism in the CC mode, the l plaintext blocks are grouped into a sequence of t processes: p = p1p2…pt such that process pj has n plaintext blocks, where1 ≤ j ≤ t–1; while the last process pt has nt plaintext blocks such that 1 < nt ≤ n. The values of n and nt are computed according to Eqs. (1) and (2), respectively.
After binding plaintext blocks to their corresponding processes, as shown in Fig. 1(a), the whole encryption process can be achieved according to Eq. (3).
Where, Mi and Ci are the plaintext block number i and its corresponding ciphertext block, respectively, and i = 1, 2, 3, …, l. The equation shows that the ciphertext block of the first block in each process pj is the encryption of the XOR of the first plaintext block in process pj and the initialization vector IVj, such that j is equal to ceiling of i divided by n (i.e., j = ⌈i/n⌉). The first plaintext block in each process is recognized when the modals value of (i mod n) is equal to one. The ciphertext block Ci of any other plaintext blocks is the encryption of the XOR of the corresponding plaintext block Mi and the preceding ciphertext block Ci−1 (e.g., Ci= Ek (Ci−1 ⊕ Mi), where i does not refer to the first plaintext block in any process. Also, the value of IVj is computed according to Eq. (4). The counter is encrypted to overcome different attacks such as differential analysis attack [15,16] that might be introduced from using a counter.
This equation finds the value of IVj by encrypting the value that resulted from adding a secret counter CT and the value of j, where j = 1, 2, 3, …, t and 1 ≤ t ≤ 16. The counter CT has the same length as the block size and it is constructed from the concatenation of two parts. The left or most significant part represents the number of processes that is going to be used. It has four bits to represent up to 16 processes. Our experiments show that dividing a plaintext into a maximum of sixteen processes is a good choice. For example, the code of one process is 0000, the code of two processes is 0001, and so on until the code of 16 processes is 1111. The right or least significant part is a positive random number that has a length equal to the block size minus four bits. When adding a value to the CT, the value will be added to the right part, which is the random value.
After finishing encrypting all of the processes, the value of counter CT is encrypted and its corresponding ciphertext C0 is concatenated with the other ciphertext, as depicted in Fig. 1(a). As noted in Eq. (3), the input for the encryption algorithm for each plaintext block has no fixed relationship to the plaintext block. Accordingly, the ciphertext blocks of the repeated plaintext blocks are different.
To demonstrate the idea, the second process p2 is chosen as an example. Since p2 is the second process and each process has n plaintext blocks, it is assigned the plaintext blocks from Mn+1 to M2n. So, the corresponding ciphertext blocks are Cn+1 to C2n. In this case, the Mn+1 is the first plaintext block in the process p2 because the value of ((n+1) mod n) is one. Therefore, Cn+1 is equal to Ek (IV (n+1)/n ⊕ Mn+1). Since the value of (n+1)/n is greater than 1 and less than 2, its ceiling will be 2 (i.e., Cn+1 =Ek (IV2 ⊕ Mn+1)). On the other hand, each ciphertext block Cn+i corresponding to the plaintext block Mn+i such that 2 ≤ i ≤ n is equal to the encryption of XORing Cn+i−1 and Mn+i (i.e., Cn+i = Ek (Cn+i−1 ⊕ Mn+i), since the value of (n+i) mod n ≠ 1).
The decryption operation, on the other hand, depicted in Fig. 1(b) starts with decrypting the ciphertext block C0 to recover the counter CT and the number of processes t used during the encryption operation. Then, in the same way, the ciphertext blocks from C1 to Cl are divided into the same sequences of t processes; each has n ciphertext blocks, except the last process has nt ciphertext blocks.
After associating ciphertext blocks to their corresponding processes, the plaintext blocks can be recovered according to Eq. (5). If a ciphertext block Ci refers to the first block in any process (i.e., when i mod n = 1), recovering the plaintext block Mi is obtained by XORing IV ⌈(i)/n⌉ and the decryption of Ci. Otherwise, the plaintext block Mi is recovered by XORing the ciphertext block Ci−1 and the decryption of Ci. To demonstrate this operation, the process p2 is chosen as an example. In this case, the process p2 has the ciphertext blocks from Cn+1 to C2n and their corresponding plaintext blocks are Mn+1 to M2n. This indicates that Cn+1 is the first ciphertext block in the process p2 because the value of (n+1) mod n is 1. Therefore, Mn+1 is recovered by XORing the decryption of Cn+1 and the initial vector IV2 (since the ceiling of (n+1)/n is 2) associated with the process p2 (i.e., Mn+1 = Dk (Cn+1) ⊕ IV2). On the other hand, each of the other plaintext blocks (i.e., all blocks Mn+i where 2 ≤ i ≤ n) is recovered by XORing the ciphertext block Cn+i−1 and the decryption of Cn+i. In other words, Mn+i is recovered as Mn+i = Cn+i−1 ⊕Dk (Cn+i). This is because that the value of (n+i) mod n is not equal to 1.
Where, i = 1, 2, 3,…, l and n is the number of blocks in each process pj such that j = 1, 2,…, t–1. Also, Dk refers to the decryption operation using the block cipher algorithm with the key k.
Since the CC mode of operation groups the blocks into processes and each process can work independently from the others, it enables parallelism and hence, improves the performance of the CC mode in terms of encryption speed over the standard CBC mode. The results in Section 4 show that the proposed CC mode of operation improves the performance over the standard CBC mode of operation during the encryption process, especially when the plaintext is too big. Also, each process can encrypt its plaintext blocks in a behavior like the CBC mode. Therefore, the CC mode provides a chain dependency within the same process (i.e., any ciphertext block, except the first block in a process, is a function of all the previous ciphertext blocks of the same process).
Even though the CC mode enhances the performance over the CBC mode, it does not produce a short authenticated code as in the CBC mode. In the CBC, the encryption of any plaintext block is a function of the previous blocks. Since the last block is a function of all the other plaintext blocks, it is used as a message authentication code (MAC). On the other hand, this is not applicable to the CC mode because the plaintext of each process is encrypted separately. In the CC mode, the last ciphertext block in each process is a function of the plaintext blocks in the same process only. Therefore, producing a MAC as a function of the last ciphertext blocks of all of the processes represents a message authentication code for the whole message or plaintext, as shown in Fig. 2.
Fig. 2 describes how the last ciphertext block in each process is used to produce a MAC in the CC mode. The top part in Fig. 2 is the same as that in Fig. 1(a), which is the encryption process in the CC mode. The down part shows how the MAC is generated. It produces the CC1 by encrypting the XORing of Cn and the counter CT. The CC2 is obtained from the encryption of XORing C2n and CC1. This operation is continued until the CCt−1 is obtained, and it is clearly defined in Eq. (6).
Finally, the MAC is found by encrypting the XORing of the CCt−1 and the last ciphertext block Cl, as described by Eq. (7).
Where, t is the number of processes used in the encryption and CCt−1 is the encryption of the XOR of the ciphertext block C(t−1)n and CCt−2, as shown in Fig. 2. This shows that before finding the MAC, CCt−1 needs to be obtained, which in turn needs CCt−2 and so on until finding CC1. Therefore, Eq. (6) is formulated to obtain CCi as a function of the Ci*n and CCi−1. The generated MAC is attached to the ciphertext obtained during the encryption operation.
The verification of MAC is achieved in two phases. The first phase gives a general indication of whether the integrity of the message is safe or not. This phase is achieved by generating a new MAC from the ciphertext in the same way as it was created before. Then, it is compared with the attached MAC. If both are the same, it gives an indication that the integrity of the message might be safe. The second phase depends on the processes. Each process verifies its own part by checking the authentication of the last ciphertext block, as in the CBC mode of operation. If the authentication verification of each process is valid, it means that the overall authentication of the message is correct.
4. Discussion
After introducing the CC mode as a new block cipher mode of operations, it is essential to compare it with the current standard modes of operation for different evaluation criteria, as shown in Table 1. These evaluation criteria include chain dependency, which refers to how adjacent plaintext blocks affect the encryption of a plaintext block; error propagation; the authentication code; confidentiality; the number of passes; parallelism; the usage of nonce; message size; and the deployed block cipher algorithm. The following sub-sections introduce the performance and security analysis of the CC mode compared to other current modes of operation.
To illustrate the performance of the CC mode against current standard modes, let’s consider the following tentative example: suppose we have a message with 1,000 blocks to be encrypted using different modes, including the CBC, CTR, CCM, and CC modes, on a dual processor machine. Assume that the block encryption time is 2 ms. In this example we also assume that the overhead of preparing the plaintext is neglected in all the modes considered hereafter, as this overhead is more or less the same for all modes and we also adopt this assumption in order to keep the illustration simple.
In the CBC mode, the expected encryption time is equal to 2,000 ms (resulting from 1,000 blocks × 2 ms spent by each block). This is due to the fact that the CBC mode does not provide parallelism since the encryption of any plaintext blocks depends on the encryption of its previous block.
In the CTR mode, the expected encryption time is 1,000 ms (500 blocks × 2 ms). Since CTR provides parallelism, the plaintext can be distributed between the two processors (i.e., each processor is assigned roughly 500 blocks).
In the CCM mode, the expected encryption time is 3,000 ms (1,000 ms spent by the CTR mode + 2,000 ms that remain in the CBC mode). This time is obtained because the CCM mode achieves its encryption through two phases of operation. The first phase uses the CTR mode to encrypt the plaintext. This phase will last up to 1,000 ms as discussed in the CTR mode. The second phase uses the CBC mode to generate a MAC. The time spent by this phase is 2,000 ms. Since the two phases are executed one after another, the total encryption time is equal to the summation of the time spent by both phases, which is 3,000 ms. By executing the two phases in parallel, this result can be improved to be 2,000 ms since we have two processors and the CCM architecture allows this.
In the CC mode, the plaintext is distributed between the two processors and each will be assigned roughly 500 blocks. The CC mode works in two phases, as shown in Fig. 2. The first phase will almost last for 1,000 ms (i.e., results from multiplying 500 blocks by 2 ms). The second phase is concerned with generating the MAC. In this configuration, it will be generated after encrypting two blocks, which refers to the last block in each process. Therefore, the time that will be taken by the second phase is 4 ms. Thus, the total encryption time of the two passes in the CC mode is 1,004 ms.
Based on the above-mentioned example we conclude that the total encryption time (2,000 ms) of a single pass CBC mode is larger than the total encryption time (1,004 ms) of the two passes of the CC mode. It is also notable that, in the CC mode, the time spent by the second pass is far less than that of the first pass. Therefore, the total time of the two passes is almost equal to that of the first pass. In conclusion, our proposed CC mode almost achieves the parallelizable performance of the CTR mode while providing the MAC for authentication. In addition, it outperforms both the single pass CBC mode and the two passes CCM mode in terms of encryption time.
In addition to improved performance, the CC mode strengths the security over the CBC mode. In the CBC mode, the same IV may be used in encrypting several messages. Thus, if the same message is encrypted again, the CBC will produce the same ciphertext. On the other hand, attacking a ciphertext with a padding oracle attack [17] depends on the IV. Using a constant IV makes the block cipher mode vulnerable to padding oracle attacks, which is the case with the CBC mode. Alternatively, our CC mode overcomes this shortcoming by using a unique and concealed IV for each message. In this way, the CC mode produces different ciphertexts, even if the same message is encrypted again. This makes the CC mode resistant not only to a padding oracle attack but also to differential analysis attacks.
Despite the effectiveness of the CTR mode in achieving fully parallelizable performance with providing message confidentiality, it lacks message authentication. Therefore, the CC mode is designed to achieve the performance of the CTR mode while providing both message confidentiality and authentication.
Finally, the CC mode achieves the security of the CCM mode since both of the modes provide a unique nonce for each message. In the CC mode, the nonce is included in the counter CT. Also, both modes provides message authentication. On the other hand, the CC mode outperforms the CCM in terms of providing better encryption time. In addition, the CC mode is designed to work with any block cipher encryption algorithm, while the CCM mode is designed to work only with 128-bit block size algorithms, such as AES128.
5. Experimental Results
In this section, we present the experimental environment and then we demonstrate our experimental results.
5.1 Environment
To verify the performance of our proposed CC mode of operation, we compared its performance in terms of encryption time with that of the CBC and CTR modes. The choice of using the encryption time as the main criterion is so that the parallelization capability of each of these modes is reflected. To achieve the required performance verification, we need a multi-processor machine. Unfortunately, such a machine was not available to us at the time of our experiment. Alternatively, we were able to use one of the methods that emulate multi-core machines [18]. In our experiment, we emulated the multi-core machine with nine machines. We used one machine as a coordinator and the other eight machines as servers, which acted as eight parallel processors, as shown in Fig. 3.
These nine machines were connected together through a Cisco baseline switch 2226 of 24 ports that made up a small Local Area Network (LAN). The coordinator machine that we used was a HP ProBook 6550b laptop, while the remaining eight server machines had the same configuration. This configuration was an HP desktop with an Intel core i5 processor (2.8 GHz), 2 GB RAM, and a 32-bit operating system as the system type. In addition, it executed Windows 7 professional as the operating system. To conduct our experiment, we developed a client-server application to coordinate among the client machine and the other eight server machines. The client machine would send the plaintext messages along with the control commands (such as selecting the encryption algorithm, used key, initial vector, and mode) to one or more machines in parallel based on the technique being tested. Each experiment was repeated 50 times and their normalized average results are reported in the next subsection.
5.2 Results
Based on the aforementioned experimental environment, we conducted three different experiments and their results are shown in Figs. 4–6. Each experiment was applied to the DES and AES block cipher algorithms. Figs. 4(a), 5(a), and 6(a) show the performance of the DES algorithm while Figs. 4(b), 5(b), and 6(b) depicts the normalized encryption time resulted from the AES algorithm.
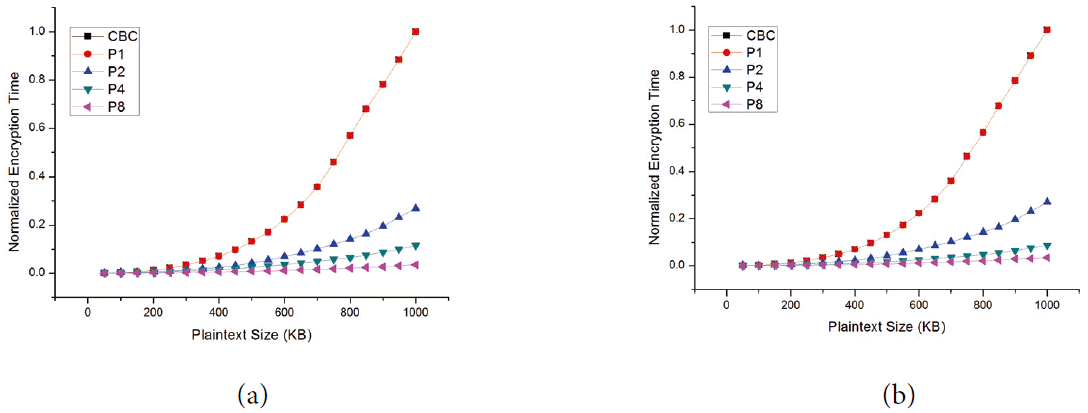
Normalized encryption time in cipher block chaining (CBC) vs. counter chain (CC) mode. (a) DES encryption in CBC vs. CC and (b) AES encryption in CBC vs. CC.
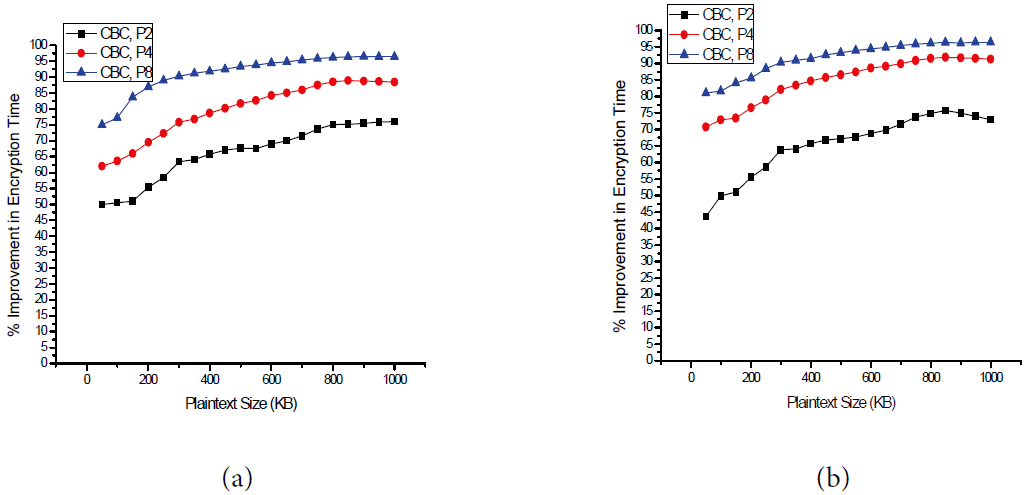
Percentage of improvement in encryption time using multi-processors in counter chain (CC) mode relative to that of cipher block chaining (CBC) mode. (a) DES improvement and (b) AES improvement.
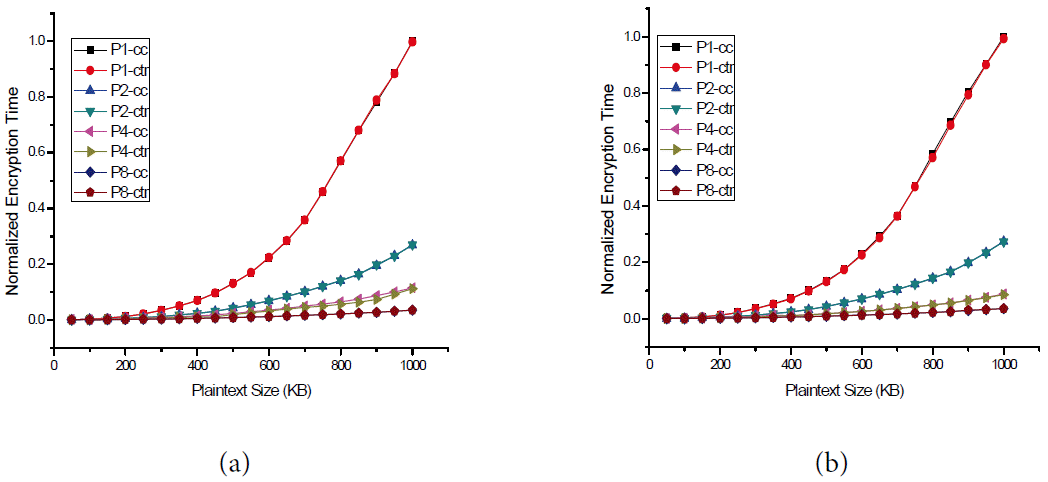
Encryption using 1, 2, 4, and 8 processors in counter chain (CC) and counter (CTR) modes. (a) DES and (b) AES.
The results of the first experiment, which are shown in Fig. 4, compared the normalized encryption time against the size of the plaintext for the CBC and CC modes. Note that due to the nature of the CBC mode, it did not support more than one processor. The results in Fig. 4 show that the increase in the normalized encryption time with the increase in message size is not linear. Moreover, similar behavior has been reported recently in [19,20]. These results also indicate that when using a single processor, the normalized encryption time in CBC is almost identical to that of the CC mode. This confirms that the proposed CC mode has a very small overhead that might be negligible when compared to the CBC mode. Furthermore, when there are two processors, the normalized encryption time of the CC modes is dramatically decreased. For example, for a message size of 600 kB, the normalized encryption time is 0.22 when using the CBC mode. For the same value of the message size, the corresponding normalized encryption time is 0.07, which represents an improvement of 68%. As calculating the improvement is more meaningful in interpreting the results, we plotted in Fig. 5 the improvement in encryption time using the CC mode for a different number of processors with respect to the encryption time using the CBC mode.
The results shown in Fig. 5 clearly indicate that our proposed mode of operation is more efficient in terms of improving the encryption time when compared to the CBC mode. Fig. 5 clearly shows that when using the proposed CC mode, the encryption time can be reduced significantly by increasing the number of processors. For example, Fig. 5(a) indicates that when the plaintext size is 200 kB, the improvements in the encryption time in the DES mode were 55.4%, 69.5%, and 87% when using two processors, four processors, and eight processors, respectively.
It is also notable that promoting the machine from a single processor to a dual processor gives the highest enhancement in the encryption time when compared to upgrading a machine from two processors to four processors or from four processors to eight processors. For example, Fig. 5(b) shows that when the plaintext size is 800 kB, the improvement in encryption time is 74.7 when replacing a single processor machine with a dual processor machine, and the enhancement improvements in encryption time are 16.7% and 4.6% when upgrading from two to four processor machines and from four to eight processor machines, respectively. This finding indicates that some hardware upgrades that cost less may lead to exceptional improvements in the encryption time and some other upgrades that cost a lot may result in insignificant improvements.
The results of the second experiment depicted in Fig. 6 show the parallelization behavior of the CC mode and CTR mode. In particular, in Fig. 6, we compare the normalized encryption time using one, two, four, and eight processors in CC and CTR modes. The results show that the normalized encryption time of the CC mode is similar to that of the CRT mode. In other words, the proposed CC mode achieves almost the same speed of the CTR mode, which is a fully parallelizable block cipher mode.
6. Conclusion
In this paper we proposed a simple and efficient block cipher mode of operation. The proposed CC mode integrates the CBC mode with the CTR mode. It uses their advantages in terms of providing an authenticated message code and parallelizable architecture while avoiding their shortcomings. Our experimental results on a multi-processor environment indicate that the proposed CC mode achieves better encryption time when compared to the CBC; especially, when there is more than one processor. Moreover, when compared to the CTR mode, the CC mode provides a similar encryption time with the advantage of providing message authentication.
Acknowledgement
This paper is supported by the deanship of scientific research at Taibah University under grant number 3040/1434.
References
Biography
Aly Mohamed El-Semary http://orcid.org/0000-0002-8698-0622
He received his B.S. degree in Systems and Computer Engineering from Al-Azhar University, Cairo, Egypt in 1992, and M.S. and Ph.D. degrees in Computer Science from Tulsa University, USA in 2001 and 2004, respectively. He works for the Department of Systems and Computer Engineering, Faculty of Engineering, Al-Azhar University, where he is currently an associate Professor. However, he is currently working as a visitor for Computer Science and Engineering College, Taibah University, Saudi Arabia. His current interests include network and computer security, sensor networks, fuzzy logic, data-mining, and neural networks. He is a member of IEEE and the author of several research papers published in the most reputable journals and conferences. He is also a working group member of IEEE 1903 standard on Next-Generation Service Overlay Networks (NGSON).

Mohamed Mostafa A. Azim http://orcid.org/0000-0001-7593-3591
He received the B.Sc. degree in electrical engineering from Cairo University, Egypt in 1994, the M.Sc. degree jointly from the Fontys University and Technical University Eindhoven, Netherlands, in 1997, and the Ph.D. degree in computer sciences from Tohoku University, Japan, in 2006. He is the associate professor of electronics technology, Beni-suef University, Egypt. In 2008, he joined the college of computer science and engineering at Taibah University, KSA. On 2012, he became the chair of networks and communications systems department. He is the author of several research papers published in the most reputable journals and conferences. He is the author of the book titled “Optical Networks: A Restoration Perspective with Active”. He is also the editor of the book titled “Wireless Sensor Multimedia Networks (WSMNs): Architectures, Protocols and Applications” published by CRC Press USA. He is a working group member of IEEE 1903 standard on Next-Generation Service Overlay Networks (NGSON). He is member of the editorial boards of the International Journal of Sensor and Related Networks and International Journal of Communication Networks and Information Security (IJCNIS).