Improving the Diffusion of the Stream Cipher Salsa20 by Employing a Chaotic Logistic Map
Article information
Abstract
The stream cipher Salsa20 and its reduced versions are among the fastest stream ciphers available today. However, Salsa20/7 is broken and Salsa20/12 is not as safe as before. Therefore, Salsa20 must completely perform all of the four rounds of encryption to achieve a good diffusion in order to resist the known attacks. In this paper, a new variant of Salsa20 that uses the chaos theory and that can achieve diffusion faster than the original Salsa20 is presented. The method has been tested and benchmarked with the original Salsa20 with a series of tests. Most of the tests show that the proposed chaotic Salsa of two rounds is faster than the original four rounds of Salsa20/4, but it offers the same diffusion level.
1. Introduction
Cryptography plays a significant role in protecting the data while the data is being exchanged over the Internet. Obviously, efficient encryption algorithms are highly sought due to the data being so large and real time requirements. Stream ciphers are one of the essential symmetric cryptography primitives, along with block ciphers. Stream ciphers are normally needed in applications where the speed of encryption and decryption is a concern.
European Network of Excellence for Cryptology (ECRYPT) was established in February 2004 with the purpose of encouraging cooperation between researchers involved in information security. eSTREAM is the stream cipher project of ECRYPT and was established in 2005 [1]. The main goal of eSTREAM is to facilitate the recommendations of secure and efficient stream ciphers for widespread and common adoption. In 2005, as a response to the call by eSTREAM for new stream ciphers, 34 stream cipher candidates were submitted and Salsa20 was one of the finalists.
The 20-round Salsa20/20 is faster than Advanced Encryption Standard (AES) and provides better security. The full version of Salsa20/20 is recommended by cipher designers for typical cryptographic applications. Along with Salsa20/20, the reduced round variants Salsa20/12 and Salsa20/8 are offered. The reduced versions of Salsa20 are among the fastest stream ciphers available and are recommended for applications where speed is more important than the level of security.
The stream cipher Salsa20/20 and its reduced rounds versions, Salsa20/12 and Salsa20/8, have been chosen by eSTREAM to be ones of the few standards for widespread adoption. However, some arguments have been raised against the usage of simple mathematical operations and XOR operations in Salsa20, as discussed by Bernstein [2].
The security of Salsa20/7 has been broken by differential attacks [3,4]. Aumasson et al. [5] concluded via cryptanalytic papers by Fischer et al. [6], that 2,151 operations are needed to break the seven rounds of 256-bit Salsa20.
Chaos theory was discovered in the 1970s with significant contributions from a variety of research areas, such as physics, mathematics, nonlinear mechanics, biology, chemistry, electrical engineering, etc. [7]. In recent years, chaotic cryptography has attracted much attention. Many efforts have been proposed by researchers to build chaotic cryptosystems. The butterfly effect and the extremely random and unpredictable nature of the chaos function is one of the most important qualities in deterministic chaotic schemes. The butterfly effect is the sensitivity to the initial states and/or control parameters of the chaotic map and unpredictability is the pseudo-random orbits produced by deterministic equations [8].
The main focus of this paper is to address the statistical leakage that has been found in the reduced version of Salsa20 by employing the chaos theory into the cipher. The proper solution is to use distinct chaotic key that is to be fed to the cipher for each block, as well as employing an XOR network into the first rounds of Salsa20. By doing so, the modified Salsa20 can achieve diffusion faster than the original Salsa20.
The rest of the paper is structured as follows: the next section will present the background of Salsa20 and the chaotic logistic map. Analysis of Salsa20’s design will be presented in Section 3. The proposed method will be explained in Section 4. An evaluation of the proposed method will be conducted and a discussion of the results will be given in Section 5. Finally, the conclusions will be presented in Section 6.
2. Background
2.1 Scope on Salsa20
Salsa 20 is a stream cipher proposed by Bernstein [9]. This cipher is designed based on a 32-bit bitwise addition (XOR), 32-bit addition, and rotation operations. The algorithm maps a 256-bit key, a 64-bit nonce, a 64-bit stream position, and four constants of a 32- to 512-bit output (key stream).
A hash function of a 64-byte input and 64-byte output is the core of Salsa20, which is a stream cipher that operates in a counter mode. A 64-byte key stream is produced by hashing the key, nonce, and block counter and the result is XOR-ed with a 64-byte plaintext. The Salsa20 hash function invokes what is called a quarter-function. Fig. 1 shows the Salsa20 quarter-function. The quarter round function can be represented mathematically by the following equations:
2.2 Chaotic Logistic Map
Many of the proposed digital chaotic ciphers have used different chaotic maps, such as the 2-D Hénon attractor in [10] and [11]. The quasi-chaotic nonlinear filter was used in [12], and the piecewise linear chaotic map was used by Hasan [13] and Wang et al. [14]. Logistic maps have been utilized in [15–17].
The logistic map is a simple mathematical quadratic polynomial of that demonstrates complex chaotic behavior. Because of its simplicity, the logistic map continues to be useful as a test bed for new ideas in the chaos theory, as well as for the application of chaos in cryptography [18]. The simple form of the logistic map can be represented mathematically, as shown in in Eq. (5):
where, x is a state variable that can have any value between 0 and 1, and r is the system parameter that lies in the interval [1, 4].
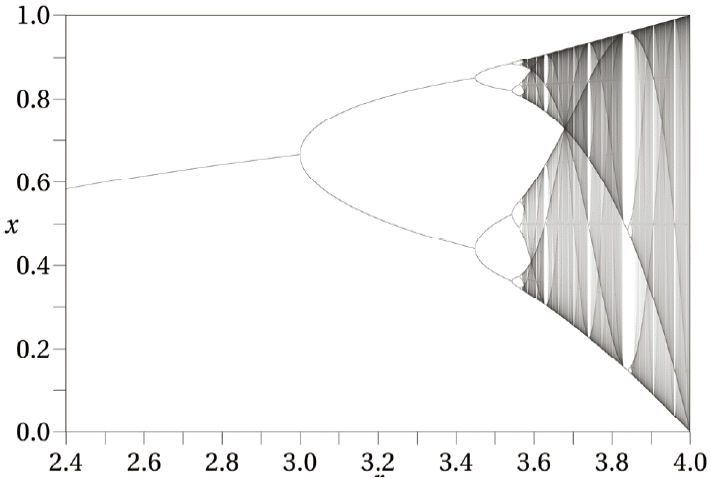
Fig. 2 shows the bifurcation diagram of the logistic map. The bifurcation parameter r is shown on the horizontal axis of the plot and the vertical axis shows the possible long-term population values of the logistic function. Each of these bifurcation points is a period-doubling bifurcation.
3. Analysis of Salsa20’s Design
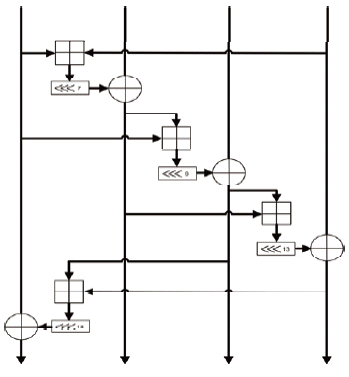
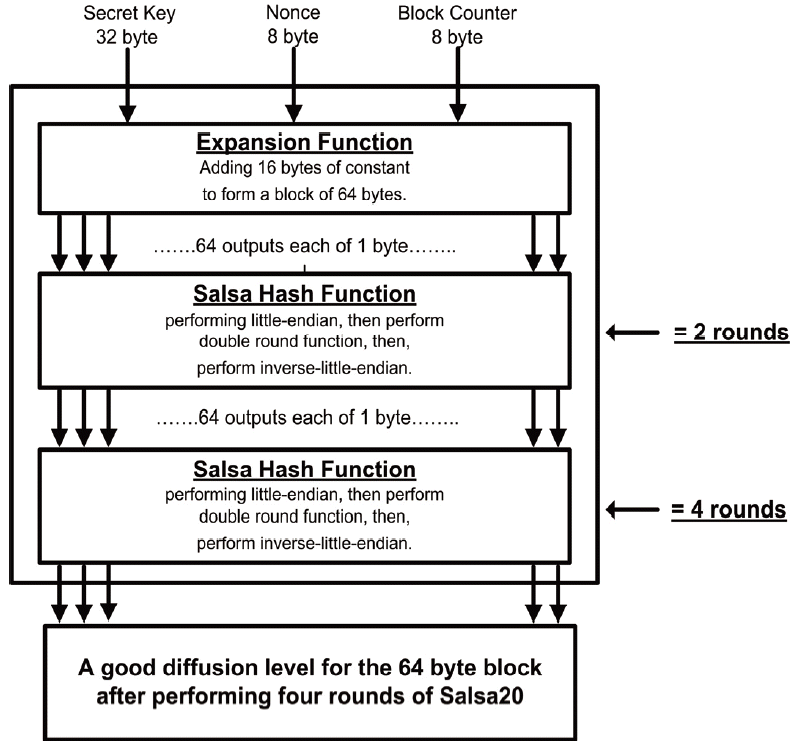
There are three inputs that are considered the seeds for Salsa20. The seeds are the 32-byte secret key, the 8-byte nonce, and the 8-byte value for the block counter. In the initial state, these seeds will be appended or mixed with 16-bytes of constants at the expansion function to make the 64-byte block. Fig. 3 shows the block diagram of Salsa20 and the four rounds of Salsa20.
The output from the expansion function is scrambled by the Salsa hash function. Actually, one call to the Salsa hash function is considered to be two rounds for Salsa20. This is because the hash function calls the round function twice. Thus, every call to the hash function is equal to two rounds of Salsa20, as pointed out in Fig. 3. After two rounds of Salsa20, only 50% of the 64-byte block is altered, as will be explained in the analysis phase.
Diffusion is one of the most important properties of a good cipher. On the subject of Salsa20, there is only 1-bit of difference at the inputs of any two sequential blocks. This difference is known as the block counter bit. Although there is a slight change at the input of Salsa20, the cipher produces a good diffusion after completing four rounds of scrambling.
By the end of the fourth round, every bit of each of the 16 words will be altered. Normally, the Salsa hash function starts with a block, which only differs from the previous block on the block counter bits. As the result, the XOR of those two blocks will be zero for all of the elements, except for the difference of the block counter. The following two matrices are example of two Salsa20 sequential blocks in which the only difference between them is the block counter number:
The XOR of these two matrices produces the following matrix:
After performing one Salsa hash function for each of those blocks and then XOR-ing them, we obtained the following result:
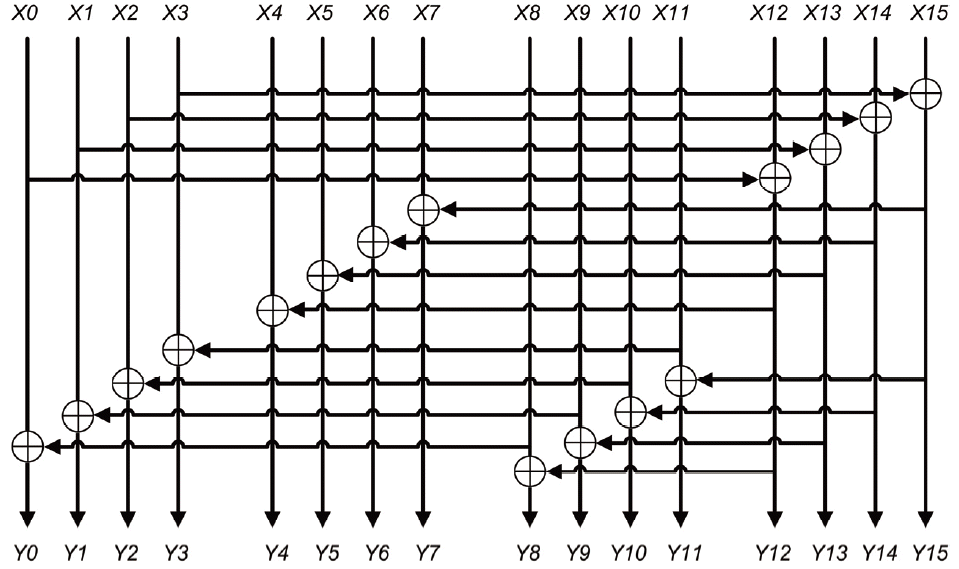
According to this analysis, it would better to ensure that each word in the Salsa20 block is scrambled before the third round is started. Thus, an XOR network is used after the second round.
One of the objectives of this study is to achieve a good diffusion level in less than four rounds. In the next section, a proposed XOR network is employed after the second round of Salsa20 to improve the randomness of the cipher by ensuring that every byte of the 64-byte block is altered.
Another weakness of Salsa20 is the fact that there is only 1-bit of difference between the input blocks of Salsa20. When the difference between any two sequential blocks is very slight (as in the case of Salsa20 where the difference is 1-bit), that slight difference could be used to perform a differential attack. In the proposed design, as what is done in the next section, a chaotic logistic map is used to generate a chaotic key, which will increase the input differences of the blocks to 33-bits.
4. The Proposed Method
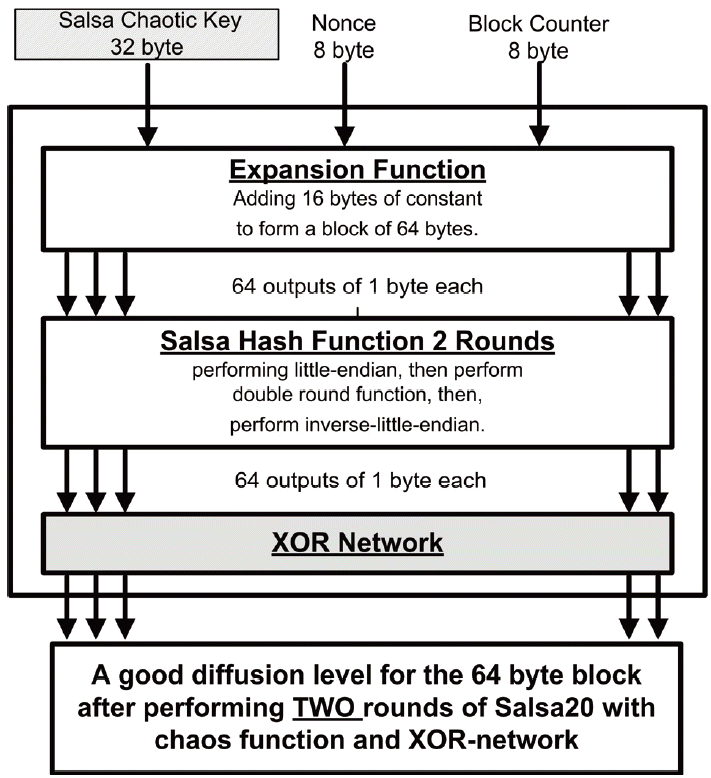
Fig. 4 shows the proposed method of improved Salsa20 by using a chaotic map. First, a 32-byte chaotic key is generated by using a specific algorithm, which will be explained in the next section. The 32-byte chaotic key, 16-byte nonce, and a block counter are mapped by using the Salsa expansion function to form an output of 64-byte. After that, the Salsa hash function is performed once. Similarly to the original Salsa20, the hash function calls the little-endian function, which converts each of the 4-bytes coming from the expansion function to one 32-bit sized word. Then, the double round is called to scramble the block. Next, each output word is converted back to four separated bytes by calling the inverse-little-endian function to have a 64-byte output block.
The output of the hash function passes through a scrambling XOR network and then, the same as with the original Salsa20, a number of Salsa hash function rounds are applied to the input block. Finally, an inverse-little-endian function is performed to convert 16 words to 64-bytes of key stream. 64-bytes of plaintext are then encrypted by XOR-ing the plaintext with a 64-byte key stream.
4.1 Chaotic Key Generation
The stream cipher Salsa20 works with two versions of key length, either 16-bytes (128-bits) or 32-bytes (256-bits). The 32-byte key length is the one preferred by the designer of the original Salsa20 and it is the one that we have used in this proposal. As with any stream cipher, Salsa20 produces a key stream that is as long as the plaintext length. The seeds that Salsa20 uses to generate the key stream are the secret key, the nonce, and the block counter as shown in Fig. 4. Each 64-byte key stream block is generated by using the same seeds with 1-bit of difference in the block counter. As previously mentioned, Salsa20 offers very good diffusion after four rounds of the Salsa hash function has been completed, which makes any two sequential blocks completely different (although, they only differ by 1-bit in the counter block).
The generation of the chaotic key will enhance Salsa20’s resistance against different attacks and it will help to remove the statistical leakage that could be detected in the first rounds. Implementing the chaotic logistic map to generate the chaotic key will increase the input differences between any two sequential blocks from 1-bit to 33-bits because every block has four new chaotic bytes. These 33 new bits come from the 1-bit, which is the block counter bit, and the other new 32-bits come from the four chaotic bytes of the secret key.
Fig. 5 shows the procedure for generating the chaotic key. The first byte of the original key is the converted integer in the range of [0, 255] to the suitable range for the logistic map, which falls in the interval of [0, 1].
Then, the resultant float value will be fed to the logistic map as input. The logistic map was chosen due to its speed the fact that it possesses the minimal computations needed to reach the chaotic behavior. The logistic map used in our proposed method is represented in Eq. (6). The three parameters that influence the map are the sensitivity constant r, the initial value x, and the iteration number n.
The high sensitivity of the logistic map to any slight change in the input, even in term of bits, leads to a huge change in the output, which results in an increase in the quality of randomness. In this proposed design the sensitivity parameter r has been adjusted to 3.82843 since the chaotic behavior of the logistic map can be observed in the interval [3.6, 4]. The bifurcation diagram of the logistic map shows the randomness behavior of the map, as shown in Fig. 2.
The chaotic output value is a float value that falls in the interval [0, 1]. The byte extraction technique is used to convert the float value resulting from the chaotic logistic map to 4-bytes. First, the bit extraction technique, which is a random walk process based on the IEEE-754 single precision binary floating point format (binary32), is used. Next, the same inverse-little-endian function of Salsa20 is used to produce 4-bytes from a 32-bit word.
The four extracted bytes from the bit extraction stage will be XOR-ed with the first 4-bytes of the original key in order to get the first chaotic key for the first block. Once the block counter starts counting for the second block, the second byte of the secret key will be chaotized using the same process to produce another four new chaotic bytes. Those 4-bytes will be XOR-ed with the next 4-bytes of the original key to make the second chaotic key for the second block. The same procedure will keep chaotizing 4-bytes of the key for every block.
4.2 XOR Network
It has been observed that it is better to have an XOR-network after two rounds of the Salsa hash function has been carried out in order to achieve a good diffusion level. As shown in Section 3, performing the hash function for only one round will leave some words untouched. The way that the network of XORs has been designed, as illustrated in Fig. 6, is to ensure that every word will be modified after the second round of the hash function has been carried out.
The output of the XOR-network will be fed to the Salsa hash function and then the other steps of the algorithm are carried on in the same way as in the original Salsa20 algorithm. Finally, a 64-byte key stream block produced from the previous process will be XOR-ed with the intended 64-byte plaintext block to produce the ciphertext.
4.3 Implementation
The proposed method was implemented in C language. The libtiff library has been used for image encryption by many other researchers. Using this library makes it easier it easier to compare the results of the original algorithm with the results of the proposed algorithm. MATLAB has also been used to perform analysis on various sets of encrypted images. MATLAB has many built-in functions for image analysis such as correlation and histogram analysis.
5. Evaluation and Discussion
The proposed method was analyzed in terms of security and speed against Salsa20/4. This analysis is detailed in the following subsections.
5.1 Security Analysis
NIST Statistical Test Suite
The National Institute of Standards and Technology (NIST) suite is a statistical test suite for random and pseudorandom number generators for cryptographic applications. The NIST suite is considered to be the most popular and is a state-of-the-art system for measuring the randomness of cryptographic applications [19].
The NIST framework, like many other tests, is based on hypothesis testing, which is the process of verifying if an assertion about a feature of a population is sensible. Regarding cryptographic applications, the hypothesis test is used to determine whether a sequence of ones and zeros is random or not. The evaluation process of a single binary sequence can be illustrated in the following steps:
State the null hypothesis by assuming that the binary sequence is random.
Compute a sequence test statistic.
Compute the p-value [0, 1].
Compare the p-value to the significant value [0.001, 0.01].
Success is declared whenever the p-value is greater than the significant value; otherwise, a failure is declared. Five out of the 15 tests of the NIST suite were chosen in this experiment. These five tests are the frequency test, frequency test within a block, rank test, linear complexity, and the entropy test. The columns of Table 1 are distributed as follows: Columns 2 to 11 show the frequency of the p-value, the next column is the computed p-value for the entire tested sample, and the last column is to show the proportion of the binary sequences that passed the randomness test.
Table 1 shows the results of the five statistical tests for Salsa20/2. Salsa20 with two rounds and Salsa20/2 did not pass any of the randomness tests by the five statistical tests.
On the other hand, Tables 2 and 3 show the results of the chaotic Salsa with two rounds (CSalsa2) and Salsa20 with four rounds (Salsa20/4). Both CSalsa2 and Salsa20/4 succeeded in passing all five tests. Thus, the results provide clear evidence that the original Salsa20 offers good diffusion after four rounds and that our proposed method does so after two rounds.
Correlation Analysis
Correlation refers to the measurement of the strength and the direction of the relationship between two sets of data. The correlation, r, which measures the strength and the direction of a linear relationship between two variables x, y can be computed mathematically, as shown in Eq. (7):
We used the correlation analysis in our research to find out how the plaintext and the ciphertext are correlated for the proposed chaotic ciphers and for the original versions of Salsa20. Generally, any plaintext has a higher correlation value that is very close to 1 or -1; whereas, the ciphertext should have the lowest correlation value for cryptographic applications. In this case, an image represents the plaintext and the encrypted version of the same image will be the ciphertext. Eq. (3) was used to determine the correlation between two adjacent pixels, as x and y represent the values of two adjacent pixels.
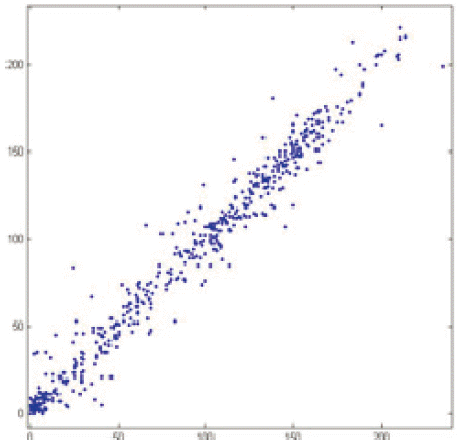
Fig. 7 represents the original image (plaintext) used in this test and the correlation of the plaintext is shown in Fig. 8. As mentioned before, the plaintext shows a high correlation between image pixels and this can be clearly seen in Fig. 8. The data displayed on the graph resembles a line rising from left to right, which means that there is a highly positive high correlation between image pixels.
The correlation values for CSalsa2, Salsa20/2, and Salsa20/4 are listed in Table 4. The correlation value of Salsa20/2 is considered to be close to that for CSalsa2 and Salsa20/4. As in the table values, it is reasonable to claim that two rounds of chaotic Salsa CSalsa2 offers a diffusion that is as good as four rounds of the original Salsa20/4. Therefore, the four rounds were shortened to two rounds with the proposed chaotic algorithm.
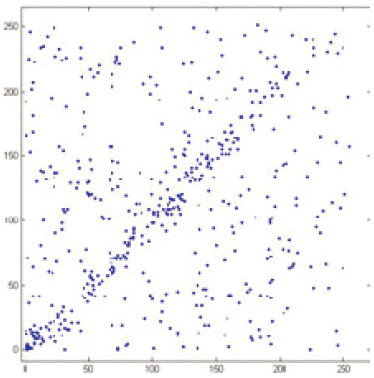
Fig. 9 shows the correlation analysis for Salsa20/2. It can be clearly seen that there is a pattern arising in the graph. However, in Fig. 10, which illustrates the correlation analysis of the chaotic Salsa CSalsa2, there is no any evidence for any pattern arising. Fig. 11 shows the result of Salsa20/4, which indicates that there is no line arising in the graph. As seen in both graphs, there are not any clues from the graphs about if the patterns are rising or falling.
Visual Testing and Histogram Analysis
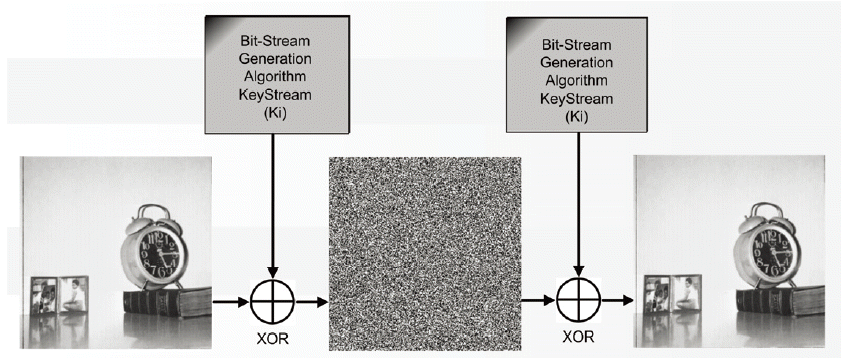
Image encryption is a very practical method that is used to test an algorithm visually. The test can demonstrate if there is any leakage in the tested cryptosystem. In the case of Salsa20 and the chaotic Salsa, performing image encryption can be done just by XOR-ing the image with the key stream produced by the algorithm. Actually, Salsa20 represents the basic principal of the stream cipher primitive that is XOR-ing the key stream with the plaintext to produce the ciphertext, which make stream ciphers very fast. Fig. 12 demonstrates how the image encryption process is performed.
Both the proposed chaotic cipher and the variants of the original Salsa20 have been visually tested by encrypting several images to find out if there is any evidence for a pattern arising in the ciphertext.
In addition to image encryption, histogram analysis has been applied for further information about the uniformity for the encrypted images with respect to the original image. A histogram is generally used to clarify the distribution of the pixel values of images. This is useful for ensuring that there are no statistical similarities between the original image and the encrypted image. Fig. 13 shows the original image that was used when we performed the visual tests. The histogram of original image, as shown in Fig. 14, illustrates large sharp rises followed by sharp declines.
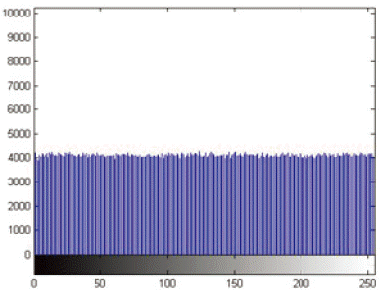
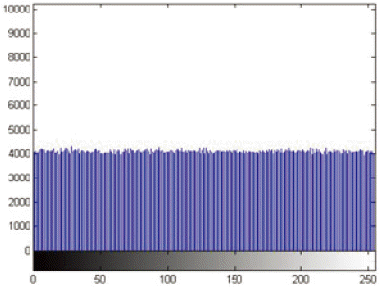
Fig. 15 shows the image encrypted by Salsa20/2. It can be clearly seen that there is a pattern arising in the image. However, in Fig. 16, which shows the image encrypted by chaotic Salsa CSalsa2, there is not any evidence of there being any leakage in the image. Fig. 17 shows the result of Salsa20/4, which indicates that there is no pattern arising in the image.
The exact same analysis procedure of image encryption as performed for histogram analysis. Fig. 18 shows the histogram analysis for the encrypted image by Salsa20/2. It illustrates large sharp rises followed by sharp declines. However, in Fig. 19, which shows the histograms of the image encrypted by chaotic Salsa (CSalsa2), the ciphertext has uniform distribution that completely differs from the original image and indicates that there are no statistical similarities between the plaintext and the ciphertext. Fig. 20 shows the results of Salsa20/4, which indicates the uniform distribution.
5.2 Speed Measurements
The speed measurement for the proposed work was performed in two different platforms—Microsoft Windows and Linux. Unfortunately, there have been many efforts to get a stable speed measurment with various timer algorithms and functions, but there are none that can give the same reading while performing the same tests several times. It has been found that the Linux platform can offer better stability than Windows. Measuring the elapsed time for a single part of the code is obtained by counting the number of clock pulses in the microprocessor while executing that code.
The speed of chaotic Salsa with two rounds (CSalsa2) was measured and compared with the original Salsa20/4 in order to evaluate the efficiency of the proposed work. The calculated average time for CSasla2 to encrypt a plaintext of size of 1MB is 0.02118 seconds, whereas the average time of Salsa20/4 is 0.02558 seconds.
5.3 Discussion
All of the security analysis and tests conducted in this research show that Salsa20 with only two rounds exhibits non-random behavior. The original Salsa20 must perform four complete rounds to achieve a good diffusion level. The statistical tests, correlation, image encryption, and histogram proved that the proposed chaotic Salsa with two rounds (CSalsa2) offers a good diffusion level.
According to the approach of this research, speed benchmarking was applied to the proposed algorithm with the original Salsa20 algorithm after concurring the proposed chaotic cipher CSalsa2 with Salsa20/4. The speed measurements show that a good diffusion level can be achieved faster by using CSalsa2.
6. Conclusion
The study set out to investigate the effectiveness of integrating the chaos theory to the stream cipher Salsa20. Salsa20 is one of the stream ciphers that can be applied for a task where the speed of encryption is as significant as the security itself. The demand for transferring huge file sizes has been increasing. As a result, securing this huge amount of data requires having systems that can encrypt that information at a high speed. The main goal of this research is to come up with a faster member of the Salsa20 family.
The proposed chaotic Salsa of two rounds (CSalsa2) needs just two rounds of data scrambling to achieve a good diffusion level, which makes the cipher faster. A novel technique of introducing the chaotic logistic map into the Salsa20 algorithm is presented in this research. The XOR-network is used to address the statistical leakage observed at the second round of Salsa20. According to the speed measurements, the proposed CSalsa2 can achieve a good diffusion level faster than the original Salsa20.
Some potentials of differential attacks could clearly evaluate the strength of the proposed chaotic Salsa in terms of security. The original reduced-round versions of Salsa20 have been corrupted by differential attacks. There is only 1-bit of difference at the inputs of any two sequential blocks of Salsa20. However, there are 33-bits of differences in the proposed chaotic Salsa system. The enlargement of the differences in the inputs can strengthen the system against different types of attacks. Therefore, performing differential attack can be an interesting subject to be done in future.
References
Biography
Mishal Almazrooie
He received his Master degree from Universiti Sains Malaysia (USM) in computer science. Currently, he is a Ph.D. candidate in computer science school in USM. His research interests include symmetric cryptography, chaos theory, quantum computing, quantum cryptography, high performance computing, GPGPU, image convolution filters, image segmentation, and clustering.

Azman Samsudin http://orcid.org/0000-0001-9981-7958
He is an Associate Professor at the School of Computer Sciences, Universiti Sains Malaysia (USM). He earned his B.Sc. in Computer Science from University of Rochester, New York, USA, in 1989. Later, he received his M.Sc. and Ph.D. in Computer Science, in 1993 and 1998, respectively, both from the University of Denver, Colorado, USA. He has been with Universiti Sains Malaysia since 1998. His research interests include Cryptography, Switching Networks and Parallel Computing. He has published more than 100 articles over a series of book chapters, professional journals and conference proceedings. He also has held a series of grants in the fields of Cryptography and Parallel Computing.

Manmeet Mahinderjit Singh
She is a Senior Lecturer attached at School of Computer Sciences, University Sains Malaysia (USM) Penang since 2012. She graduated with a Ph.D. from the University of Queensland, Australia in 2012. Dr. Manmeet research interest includes Computer & Mobile Security, Trusted System Models and Sensor Networks, RFID, etc. Dr. Manmeet also teaches courses such as Computer Security & Cryptography, System Protection & Cryptography and Business Intelligence & Data Mining.