Sparse Channel Estimation of Single Carrier Frequency Division Multiple Access Based on Compressive Sensing
Article information
Abstract
It is widely accepted that single carrier frequency division multiple access (SC-FDMA) is an excellent candidate for broadband wireless systems. Channel estimation is one of the key challenges in SC-FDMA, since accurate channel estimation can significantly improve equalization at the receiver and, consequently, enhance the communication performances. In this paper, we study the application of compressive sensing for sparse channel estimation in a SC-FDMA system. By skillfully designing pilots, their patterns, and taking advantages of the sparsity of the channel impulse response, the proposed system realizes channel estimation at a low cost. Simulation results show that it can achieve significantly improved performance in a frequency selective fading sparse channel with fewer pilots.
1. Introduction
In a typical wireless scenario, the transmitted signal arrives at the receiver via various paths of different lengths. This leads to inter-symbol interference (ISI) and creates a major difficulty for information decoding. Furthermore, using the traditional single carrier modulation with the time domain equalization approach is unattractive for wide-band system due to the high complexity of the receiver. Instead, the frequency domain equalization technology is a good choice for wide-band wireless communication system (e.g., for orthogonal frequency division multiplexing (OFDM) [1]). OFDM has been widely applied in wireless communication systems because of its high bandwidth efficiency and relative robustness against multipath fading and delay. However, it suffers from a large peak to average power ratio (PAPR).
On the other hand, single carrier modulation with frequency domain equalization, which attempts to approach the performance and complexity of OFDM while maintaining a lower PAPR as compared to OFDM, is another excellent technology for broadband systems. Single carrier frequency division multiple access (SC-FDMA) [2] is the multiple access form of single carrier modulation with frequency domain equalization Lately it has received a lot of attention and has become an alternative to orthogonal frequency division multiple access for 4G technologies. SC-FDMA has been adopted for the uplink transmission technique in both 3GPP Long Term Evolution (LTE) and LTE Advanced standards [3]. Since most of the cost in communication terminals comes from the power amplifier, a lower PAPR, which is the advantage of SC-FDMA, can significantly reduce the cost of mobile units. This results in more power efficient and less complex mobile terminals. Since the orthogonal frequency division multiple access (OFDMA) is used in the downlink, both the burdens of the complex frequency domain equalizer needed for the SC-FDMA and accommodating large PAPRs in OFDMA rest upon the base station.
Channel estimation is critical to the performance of coherent SC-FDMA demodulation; channel estimation, which is also related to diversity reception; the optimum match receiver design; and adaptive link technologies. All of these technologies require good channel estimation support. Therefore, accurate channel estimation can significantly improve the performance of the SC-FDMA system [4,5]. However, numerous experimental studies undertaken by various researchers in the recent past have shown that wireless channels associated with a number of scattering environments tend to exhibit sparse structures in the sense that majority of the channel taps end up being either zero or below the noise floor when operating at large bandwidths and symbol durations and/or with a large plurality of antennas [6–8]. However, traditional training-based methods that rely on linear reconstruction schemes at the receiver seem incapable of exploiting the inherent low dimensionality of such sparse channels, thereby leading to overutilization of the key communication resources of energy, latency, and bandwidth. A number of researchers have tried to address this problem in the recent past and have proposed training signals and reconstruction strategies that are tailored to the anticipated characteristics of sparse multipath channels [6–9]. Recently, there has been a growing interest in compressed sensing (CS) [10], which has been widely applied in many areas such as image processing, communication systems, and so on. According to the CS theory, if a signal has a sparse representation in a certain space, one can sample the signal at a rate that is significantly lower than the Nyquist rate and reconstruct it with high probability by applying optimization techniques. The essence of pilot assisted channel estimation in OFDM systems is to reconstruct the channel frequency response from pilot symbols. Hence, it is natural to consider using the CS theory in pilot-assisted sparse channel estimation to reduce the number of pilot symbols. In [11–14], the CS theory has been employed for sparse channel estimation in OFDM systems. However, litter work has been found in the SC-FDMA system. This paper will investigate the application of compressive sensing in the SC-FDMA system.
The rest of paper is organized as follows: in Section 2 we review the general SC-FDMA system model and give the problem statement. In Section 3 we present compressive sensing and pilot design in SC-FDMA. Section 4 introduces several recovery methods of compressive sensing and analyzes its complexity. Finally, Section 5 presents the simulation results and concludes our work.
2. Problem Statement
2.1 SC-FDMA
Fig. 1 depicts the high level model of an SC-FDMA receiver and transmitter [2,3]. M modulated source symbols are converted to frequency domain. The frequency domain symbols are then mapped onto M out of N (M<N) possible orthogonal subcarriers. Subcarriers can be mapped in the following two ways: localized mapping, where each user is assigned a set of m consecutive subcarriers; and distributed mapping, where subcarriers assigned to the user are equally spaced across the entire channel bandwidth. After converting the symbols back to the time domain using an N-point IDFT and inserting the cyclic prefix, the SC-FDMA time domain symbol is transmitted through the channel. At the receiver all of the steps are reversed. The crucial difference between the SC-FDMA and OFDMA comes from the additional DFT block before subcarrier mapping. The DFT block ‘spreads’ the modulated source symbols, so that each subcarrier in the frequency domain contains information about all the source symbols.
2.2 Formulation of Channel Estimation
Let’s consider a frequency selective fading channel model whose coherence time is much larger than the SC-FDMA symbol duration and the multi-path delays are sampled equispaced. Then, the multipath channel can be modeled as a finite impulse response (FIR) filter:
where L is the total number of taps and hl is the l th tap’s complex gain. Assume that the channel is sparse, which means the vector h = [h0, h1,…, hL−1]T has only a few nonzero elements; but the location of the nonzero taps is not determined.
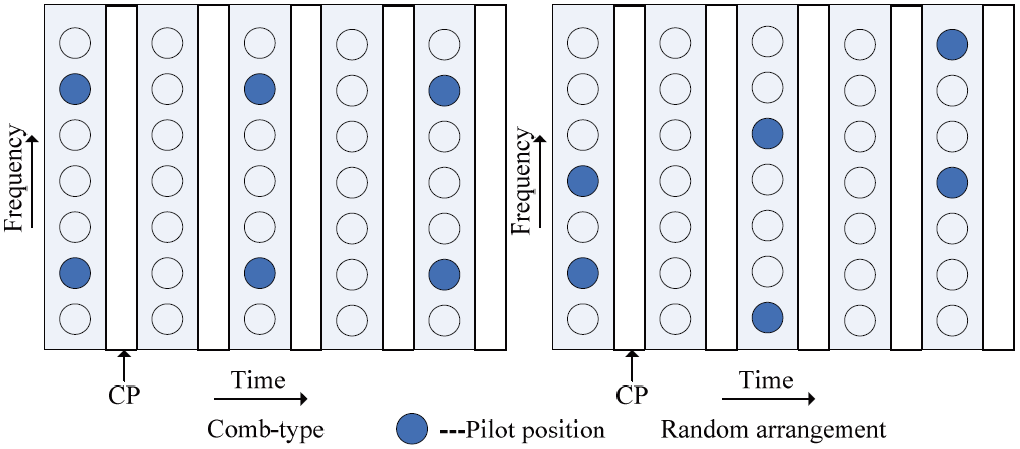
To simplify the analysis, let’s consider one user. Suppose that the SC-FDMA system consists of N sub-carriers amongst which K sub-carriers are reserved for pilot symbols, as shown in Fig. 2. The pilot inserting method is known as the Frequency Expanding Technique [15]. Generally, a comb-pilot pattern is used, as shown in Fig. 3, and the length of the cyclic prefix (CP), LCP, is not less than L.
At the receiving end, after the CP has been synchronized and deleted, it is convenient to get a matrix formulation of an SC-FDMA system as:
where Y is the reception block signal in the frequency domain of length N, and X = diag(S0, S1,…SN−1), H ∈ CNX1 is the frequency domain representation of h, and F ∈ CNXL is the FFT matrix:
where
3. Sparse Channel Estimation Based on Compressive Sensing
3.1 Review of Compressed Sensing
The CS theory [10] has recently become widely popular for improving system efficiency in the signal processing community, such as video coding, compressed image and sensors. We will now provide a brief review of sparse signal reconstruction with the CS theory.
Generally, signal processing problems are mapped into a linear observation model consisting of some linear transformation of a sparse vector, such as:
where Φ ∈ RKXL, while h is S-sparse (i.e., no more than s of its elements are nonzero). Obviously, if K< L or rank(Φ)< L, the system of equations is underdetermined and the solution is not unique. However, we have the additional knowledge that h is sparse. Thus, we search over the solution space for the sparsest solution, as shown in the following optimization problem:
where ||h||0 is the mean operation of the 0-norm, which is defined to be the number of nonzero entries in h. This optimization problem is generally combinatorial in nature. A number of authors [16,17] have proposed a more tractable relaxation of it, namely:
where ||h||1 is the mean operation of the L1-norm of h. This is a convex optimization problem that can be solved using the standard algorithms basis pursuit (BP) [16]. Eq. (5) is equivalent to Eq.(6) which has a unique solution, and the measurement matrix Φ, after scaling, needs to satisfy the restricted isometry property (RIP) [17,18]:
where ||h||2 is the mean operation of the L2-norm of h. For all S-sparse vectors h ∈ RL, for any δS ∈ (0,1), and any c1 < δS (3 −δS) 48, set
Solving the optimization problem in Eq. (6) is computationally expensive and is not suitable for real-time applications. Faster and more efficient reconstruction algorithms that use iterative greedy-based algorithms at the expense of slightly more measurements, such as matching pursuit [21], orthogonal matching pursuit (OMP) [22], and CoSaMP [23], exist.
3.2 Measurement Matrix and the Pilot Pattern Design
According to Section 3.1, designing the measurement matrix Φ with RIP would lead to the stable recovery of sparse signals h from noisy observations y. In [8] the system is modeled in the time domain directly in terms of the channel coefficients. Therefore, to identify the frequency-selective channel, it is becomes equivalent to designing the (discrete) input probe of the time-domain Toeplitz convolution matrix, which satisfies RIP. The channel coefficients are estimated from Toeplitz channel measurements. However, the Toeplitz convolution matrix increases the computational complexity.
In this paper, a random pilot matrix with RIP is presented to reconstruct the sparse channels. According to [11], measure matrices that satisfy
where YP = QY, XP = QXQH, FP = QF, Wp = QW and YP ∈ CKX1, XP ∈ CKXK, FP ∈ CKXL, Wp ∈ CKX1. Here, YP, XP and FP are all known to the receiver. Commonly, the coefficients of the channel are estimated directly (i.e., if K ≥ L, the vector h is invertible). This is a simple linear estimator in the observations where the least squares (LS) [24] channel estimator is given by:
If K< L, the performance of LSE will be poor, especially when h is a sparse vector the estimated performance will be very bad for not using the sparse property. In this case, the LS channel estimator is given by:
According to Eq. (9), it is known that this is the compressive sensing system model that was introduced in Section 3.1, where the measurement matrix is XPFP, which is determined by the pilot symbols and pilot locations. If XPFP satisfy the RIP, then we can solve it with a compressive sensing recovery algorithm such as BP, OMP, lasso, and so on. With Q generated by selecting K rows from a NXN unit matrix randomly, the channel is probed randomly with the random sequence {P(i)} in the frequency domain. {P(i)} are i.i.d. realizations from a zero mean, unit variance distribution, and P(i) ’s take values are +1 or –1 with a probability of 1/2 each. The positions in the input probe in this case match with the matrix Q, where K ≥ c2Slog L satisfies the RIP of order S with the parameter δS with the probability being at least 1−e−c1K. The insertion method for random pilots is demonstrated in Fig. 3.
3.3 Performance Analysis
Assuming the noise variance is deterministic, it is possible to obtain a reliable estimator of h as a solution to the convex program. Let Φ = XPFP be an observation matrix satisfying RIP of order 2S such than
will obey:
where hS is the best s-sparse approximation to h; the nonzero components in hS are the s largest components of h, and
Let SK be the set of indices of S nonzero entries of h, which can be termed the channel sparsity pattern of s-sparse channel. Assume that the channel sparsity pattern and the corresponding virtual coefficients h are deterministic but unknown. Then Φ̃SK is a submatrix obtained by extracting the position of observation matrix Φ corresponding to the indices in SK and the mean square error (MSE) of the proposed channel estimator can be low bounded as [19,25]:
where σ2 is the zero-mean white Gaussian with variance, γ is the pilot symbol energy, and tr(.) denotes the trace operator. The performances of the proposed channel estimator are better than that of the LS channel estimator with the MSE as
4. Simulation Results
In this section, Monte Carlo simulations are conducted to show the channel estimation performance of the proposed algorithm. To begin with, assume that a symbol block in the system of SC-FDMA is time-invariant, the length of the symbol block is N = 512, the maximum channel length is L = 64, and the number of pilot is K. The multi-path channel has the characteristics of negative exponential power delay. That is, each path power is δl2 = exp(−4l/Ncp), l = 0,1,…L −1, where Ncp = 64 is the length cyclic prefix; the number of nonzero channel taps V = 4; and the system is synchronized to the first path. This means that h0 is always nonzero, and other path delays are randomly distributed over the entire channel length of L.
In order to evaluate the performance of the channel estimation algorithm, we defined the channel estimation of the normalized mean square error (NMSE) as follows:
In fact, the direct assessment in the frequency domain is mainly because the SC-FDMA system implements equalization in the frequency domain.
First, in order to evaluate the effectiveness of CS algorithms, we compared the MSE of LS and CS with a different recovery algorithm under a different pilot. For the LS estimator, the comb-type pilot arrangement can make the channel estimation optimal; therefore, the comb-pilot is used. For CS algorithms random pilots are used. Figs. 4 and 5 show the MSE performance of LS and CS under the pilot numbers K = 16 and K = 24 . As can be seen from the figure, when the LS algorithm uses a small number of pilots, (i.e., K< L ), the algorithm is basically in an invalid state and the system would have serious errors. That’s because the LS channel estimation method requires the insertion of a pilot number that is not lower than the actual channel length, which requires K ≥ L = 64. In Figs. 4 and 5, the performance of LS with pilot number K = 64 is also given. It is evident that the LS algorithm improves greatly when K ≥ L.

Normalized mean square error (NMSE) performance of least square (LS) and compressed sensing, pilot number K=16. SNR=signal-to-noise ratio, OMP=orthogonal matching pursuit, CoSaMP= compressive sampling matching pursuit, BP=basis pursuit.

Normalized mean square error (NMSE) performance of least square (LS) and compressed sensing, pilot number K=24. SNR=signal-to-noise ratio, OMP=orthogonal matching pursuit, CoSaMP= compressive sampling matching pursuit, BP=basis pursuit.
In addition, we can see from Figs. 4 and 5 that the three CS-based recovery algorithms all have a better performance when a small number of pilots are used. Moreover, the OMP algorithm performs better than BP and CoSaMP does. The OMP algorithm uses a fast iterative mode to achieve better speed than BP. Although the calculation amount of CoSaMP is also small, its performance is quite different with the other two algorithms. Therefore, in a real system application, the OMP algorithms can be considered for recovering the channel response for their low complexity. Even more importantly, the need of the pilot is very small. Therefore, the transmission efficiency of the system can be improved greatly.
As shown in Figs. 4 and 5, we can also see that the recovery performance of the algorithm depends on the number of pilots. Therefore, we simulated the CS recovery performance of the algorithm under a different number of pilots in order to study the relationship between them. Fig. 6 shows the NMSE curve of channel estimation with a different number of pilots and the SNR of the SC-FDMA system is fixed at 15 dB. From Fig. 6 it can be seen that the estimated performance of LS is poor when the pilot is less than the channel length. When it is only close to or greater than the channel length, it has better performance; and when the pilot number is more than the channel length, the increase in performance is not obvious. For the CS recovery algorithms, a small number of pilots can get a better performance as compared to LS. However, when the pilot number is greater than about 20, the increase in performance is not very obvious. Based on our experience, the recommended number of pilots is 4–5 times the number of nonzero channel taps. Therefore, there is a tradeoff between the system transfer efficiency and performance.

Normalized mean square error (NMSE) performance of different number of pilots. LS=least square, OMP=orthogonal matching pursuit, CoSaMP=compressive sampling matching pursuit, BP=basis pursuit.
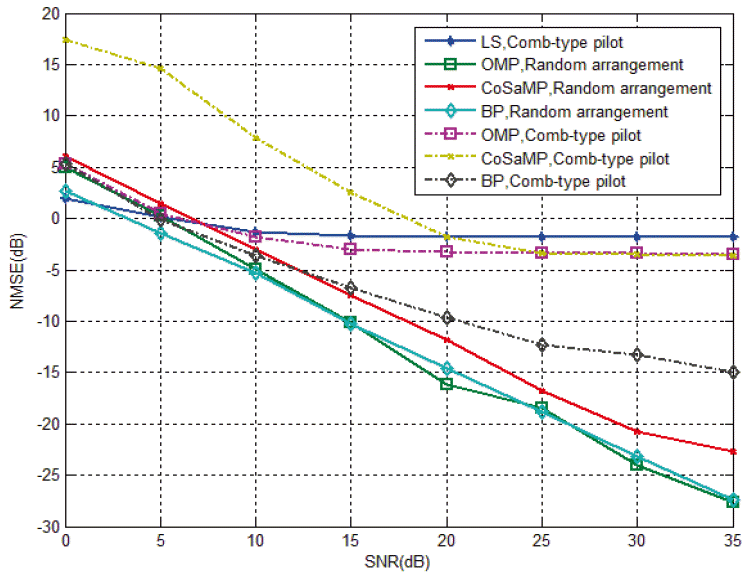
Finally, the impact of pilot arrangement on system performance is evaluated in Fig. 7. For the LS estimation, a comb-type pilot arrangement is used, and it has the best performance. Whereas, with regard to the CS algorithm, the sensor matrix needs to meet RIP constraint as we have already discussed. Therefore, a random arrangement pilot is used, as shown in Fig 3. For the sake of contrast, the NMSE of CS when using the comb-type pilot is also shown, and the pilot number K = 24 is selected. Fig. 7 shows the performance comparison of the two arrangements. It can be seen that randomly arranging the pilot results in better performance. However, randomly selecting the pilot brings about the increasing of complexity. In practice, the receiver needs to store the random pilot pattern, which increases the system storage capacity. In [14] the optimal pilot pattern is designed by minimizing the mutual coherence of the measurement matrix. This idea can be borrowed to further improve the performance of estimation.
5. Conclusion
In this paper, a CS based channel estimation algorithm is presented for the sparse channel in the SC-FDMA system. The proposed scheme, using a novel random pilot matrix pattern and the CS algorithm, has lower NMSE with fewer pilots. The analysis and simulation results verify that the proposed algorithm is effective in improving the system utilization of the spectrum. The algorithm can be applied to a wireless SC-FDMA system, such as LTE, with no extra architectural changing.
Acknowledgement
This work was supported in part by the Fundamental Research Funds for the Central Universities of China under Grant No. CDJZR12160015 and No. CDJZR12160005, and also supported by Key Program of Natural Science Foundation of Chongqing under Grant No. CSTC2013JJB40004, China.
References
3GPP TS 36.201 version 11.1.0, LTE Physical Layer - General description (Release 11), 2013
Biography
Yuan-Hong Zhong
He received his B.S., M.S., and Ph.D. degrees in communication engineering from Chongqing University, Chongqing, China in 2003, 2006, and 2011, respectively. And now he works in the School of Communication Engineering at Chongqing University. His research interests include wireless communication, wireless multimedia sensor network, and computer vision.

Zhi-Yong Huang
He received his Ph.D. degree in circuit and system from Chongqing University, in 2010. He is currently an associate professor in the School of Communication Engineering at Chongqing University. His research interests are in the areas of network security, communication system and control system.

Bin Zhu
He received his Ph.D. degree in communication and information system from Chongqing University, in 2010. He is currently an associate professor in the School of Communication Engineering at Chongqing University. His research interests include in the areas of wireless sensor network, communication system and wireless communication network.

Hua Wu
He received his Ph.D. degree in communication and information system from Chongqing University, in 2009. And now He works in the School of Communication Engineering at Chongqing University. His research interests include wireless communication, filter bank and computer vision.