Age Invariant Face Recognition Based on DCT Feature Extraction and Kernel Fisher Analysis
Article information
Abstract
The aim of this paper is to examine the effectiveness of combining three popular tools used in pattern recognition, which are the Active Appearance Model (AAM), the two-dimensional discrete cosine transform (2D-DCT), and Kernel Fisher Analysis (KFA), for face recognition across age variations. For this purpose, we first used AAM to generate an AAM-based face representation; then, we applied 2D-DCT to get the descriptor of the image; and finally, we used a multiclass KFA for dimension reduction. Classification was made through a K-nearest neighbor classifier, based on Euclidean distance. Our experimental results on face images, which were obtained from the publicly available FG-NET face database, showed that the proposed descriptor worked satisfactorily for both face identification and verification across age progression.
1. Introduction
Face recognition across age progression is a recent topic of growing interest, especially for applications in which age compensation is required, such as for identifying missing children, conducting surveillance and detecting multiple enrolments, where subjects are either not available or are trying to hide their identity. In such applications, there may be a significant age difference between the query image and those stored in the database, and it may be impossible to obtain the subject’s recent face images to update the database. Developing age-invariant face recognition systems would avoid the necessity of updating large facial databases with more recent images.
Aging-related variations have two main characteristics that influence the process of dealing with these types of variations and that make it a challenging task. First, the effects of aging cannot be controlled because it is not possible to eliminate aging variations during the capturing of a face image and collecting the appropriate training data for studying the effects of aging requires a long time. Second, both the rate and kind of age-related effects differ for different individuals and it is in combination with external factors, like health conditions and lifestyle, which have been shown to contribute to facial aging effects [1]. These particular features make the aging problem a challenging research task.
Unlike studies on other effects on face recognition systems, like illumination, facial expressions, and pose changes, there are few studies that have been carried out on face recognition across age progression. One of the principal causes for this has been the lack of public databases containing images of individuals at different ages. To the best of our knowledge, the only two largest publicly available face datasets are the MORPH [2] and FG-NET (Face and Gesture Recognition Research Network) [3] databases. Unfortunately, these databases include other issues like poses, illumination, and expressions, along with the poor quality of old photos. Therefore, proposed approaches must take these problems into account.
The existing age-dependent face recognition methods include two major categories [4]. The approaches in the first category are called “generative” since they apply a computational model to simulate the aging process to offset the impact of aging on face texture and shape, and then later apply recognition algorithms to obtain the query identity. The other category includes “non-generative” approaches [4], which concentrate on defining discriminatory features and projection methods that are minimally affected by temporal variations to allow for the accurate identification of an individual.
In this paper, we focus on non-generative methods. Our proposed method integrates Active Appearance Models (AAMs) [5] to extract a free-shape representation of the image texture, a two-dimensional discrete cosine transform (2D-DCT), and the multiclass Kernel Fisher Analysis (KFA) [6] for dimension reduction.
The rest of the paper is organized as follows: Section 2 gives a brief review of some works dealing with aging problems, and Section 3 presents the steps constituting our proposed approach. Section 4 provides information on the experimentation we carried out, and presents results and comparisons. Section 5 concludes the paper.
2. Related Works
This section outlines some earlier works that have been carried out in regards to the aging impact on face recognition systems. As we mentioned earlier, age-invariant face recognition methods are divided into two parts: generative and non-generative methods.
As an example of the first class, Ramanathan and Chellappa [7] built a system for modeling the aging process in adulthood. They built a muscle-based geometrical change model that describes changes throughout adulthood, and they characterized facial wrinkles and other skin traits that can be observed during different ages by using an image gradient-based texture transformation function.
Park et al. [8] proposed a 3D generative facial aging model for age-invariant face recognition. In this modeling technique, the query image is transformed to the same age as the database images using the trained 3D aging model.
As example of methods belonging to the second category, Ling et al. [9,10] proposed a face descriptor based on image gradient orientations taken from multiple resolutions combined with a support vector machine (SVM) as a classifier for face verification throughout all stages of the aging process. The proposed approach was tested using two private passport databases to study how increasing age gaps affects the verification performance. They also studied the effects of age-related issues, such as image quality, presence of spectacles, and facial hair.
In the same context, Mahalingam and Kambhamettu [11] developed a non-generative approach in which they defined a face operator by combining the local binary pattern (LBP) at each level of the Gaussian pyramid constructed for each face image, and the classification was performed using the AdaBoost classifier. Singh et al. [12] presented an age transformation algorithm for minimizing the variation in facial features caused by aging that registers the gallery and query face images in a polar coordinate system. Biswas et al. [13] created a verification algorithm that analyzes the coherency of the drifts in the various facial features to check if two images taken at different ages are for the same individual or not.
Additionally, Mahalingam and Kambhamettu [14] proposed an age-invariant face recognition approach using a graph-based face representation that contains geometry and the appearance of facial feature points. The aging model was constructed by using Gaussian mixture models for each individual to model their age variations in shape and texture. Their recognition approach consists of two steps: In the first step, the search space was reduced and the potential candidates were effectively selected by using a maximum a posterior (MAP) for each individual aging model. They exploited the spatial similarity between graphs using a simple deterministic algorithm for matching in the second step.
Bereta et al. [15] evaluated the local descriptors that are commonly used in face recognition, such as LBP, multi-scale block LBP (MBLBP), and Weber local descriptor (WLD), in the context of age progression. In their study, classification was carried out by calculating a distance between feature vectors containing local textures involving various similarity measures, such as Euclidean, cosine, correlation, etc. Their results showed that the Gabor coded MBLBP feature combined with the Euclidean distance yielded the highest recognition accuracy.
Sungatullina et al. [16] presented a multiview discriminative learning (MDL) method that learns about a latent low dimensional subspace. It does so by projecting three local features (SIFT, LBP, and GOP) into a common feature space, such that the correlations of different feature representations of each sample are maximized, the within-class variation of each feature is minimized, and the between-class variation of each feature is maximized.
Inspired by Elastic Bunch Graph Matching (EBGM) [17], Yang et al. [18] proposed a method called texture embedded discriminative graph matching, which formulated age-invariant face recognition as a graph matching problem. In their approach, each face is represented as a texture embedded graph, the nodes of the graph present the texture of a face area around a set of fiducial landmarks of the face, and the edges correspond to the geometric topology of the face (they represent the relative distances between the nodes). For each area, they extracted discriminative age-invariant features using the local Gabor binary pattern histogram sequence (LGBPHS) that was projected in a Linear Discriminant Analysis (LDA) subspace. An objective function was then designed to match graphs for registration and identification.
For the same purpose, Juefei-Xu et al. [19] demonstrated that the periocular region is more stable than the full face for all ages. They presented a feature extraction approach for age-invariant face recognition by applying a robust Walsh-Hadamard transform encoded local binary pattern (WLBP) on a preprocessed periocular region, followed by an unsupervised discriminant projection (UDP) for subspace modeling.
3. Proposed Approach Description
In this section, we present the details of our proposed method so as to get age-invariant features. After the crucial step of pose correction using AAMs [5], we applied a 2D-DCT on entire face images and some of the first low frequency coefficients were discarded. The remaining coefficients were used as feature vectors, and then we performed a KFA [6] to reduce dimensionality and obtain an age-robust feature. The K-nearest neighbor classifier performed the classification. The selection of coefficients was made in zigzag manner.
3.1 Aging Database
For the experiment described in this paper, we used the FG-NET aging database [3], which is a well-known database that is used to evaluate facial aging models. The FG-NET aging database is a publicly available image database containing face images showing a number of subjects at different ages. The database has been developed as an aide for researchers who study the effects of aging on facial appearance and their effects on the performance of face recognition systems. The database contains 1,002 images from 82 different subjects ranging in age from newborns to 69 years old. Typical images from the database are shown in Fig. 1. Data files containing the locations of 68 facial landmarks that were identified manually and the age of the subject in each image are also available.
3.2 Face Normalization in Images
The normalization step for the original images is an important first step for obtaining successful results. We used the same approach as for AAMs [5,20], which is described below.
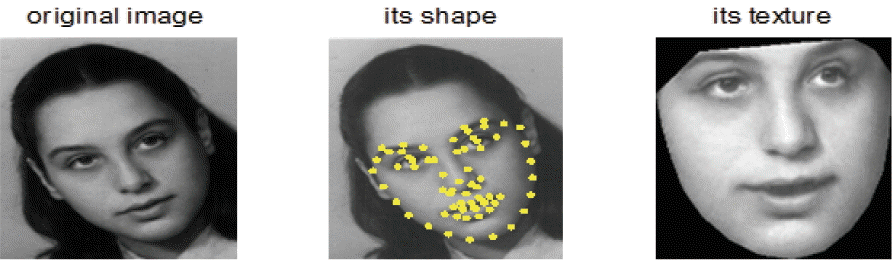
All the face images in the FG-NET database are annotated with 68 facial landmarks. A set of these landmarks is called “shape,” and the set of pixels in a gray level inside this shape is called “texture,” as shown in Fig. 2.
Shape alignment: This includes the translation, scaling, and rotation of all shapes to represent them in the same referential (Fig. 3). The classical solution to align shapes in a common referential is the Procrustes analysis method [20]. A simple iterative approach is described in Fig. 4.
Aligning two shapes (Step 4 in Fig. 4), s1 to s2, consists of finding the parameters of the transform T, (i.e., scale coefficient s), rotation angle θ, and translation (tx,ty)that when applied to s1 best align it with s2, and thereby minimizing the Procrustes distance metric:
with respect to s, θ and (tx,ty).
Cootes and Taylor [20] proposed a simple method to estimate s and θ, as follows:
then, the rotation angle and the scale coefficient are given by:
Warping image texture: Once all of the shapes are aligned into a common frame, this step makes it possible to make texture independent from the variations of the shape. In other words, we wanted to get a free shape representation of texture. For a given shape in an image, we extracted the texture and warped it to the mean shape, which was calculated in the previous step. Delaunay triangulation was used in the mean shape to establish triangles that will be used to warp texture (see Fig. 5). The method that we used was a piece-wise affine transformation, where each pixel belonging to a triangle is mapped into the corresponding triangle in the mean shape using barycentric coordinates [20].
Images were rotated to get eyes at fixed points in an image so that the inter-ocular segment was horizontal. This was based on files of eye coordinates that were provided with the original FG-NET database.
Images were resized to 128×128. Fig. 6 shows the face images in Fig. 1 after normalization.
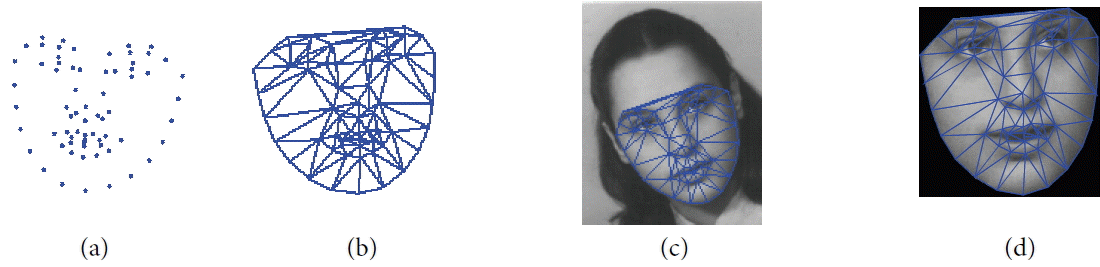
Warping texture example. (a) The mean shape, (b) Delaunay triangulation of the mean shape, (c) current image, and (d) warped texture.
3.3 Feature Extraction
In order to obtain the feature vector from a preprocessed image using AAM, we applied a 2D-DCT, and we only kept a subset of coefficients. The number of selected coefficients was chosen such that they could represent a face. Our purpose was not to reduce the dimensionality of the data, but to discard coefficients that represented too much of the texture details. The selected features that construct the feature vector were represented as points in high dimensional space, and we performed KFA to reduce dimensionality. The description of KFA is given in Subsection 3.5. The details of the DCT method are presented in the following subsection.
3.4 Two-Dimensional Discrete Cosine Transform
DCT is a powerful mathematical transform used for numerous applications in image processing applications, such as image coding, and is used for feature extraction in several studies on face recognition [21,22]. Diverse classes of DCT have been proposed [23]. In particular, the DCT was categorized [23] into four classes: DCT-I, DCT-II, DCT-III, and DCT-IV. DCT-II is the most common variant of DCT applied in signal coding, especially in compression, since it was the main idea in JPEG compression [24].
The DCT transforms an image from the spatial domain to the frequency domain. The 2D-DCT for input image A is defined as follows:
and the inverse transform is defined as:
where:
and:
M and N are the row and column size of A.
The DCT has a very important feature—it helps to separate the image into parts of differing importance. After the original image has been transformed, its DCT coefficients reflect the importance of the frequencies that are present in it. The DC-coefficient (the very first coefficient) shows the total illumination of the image, low frequency DCT coefficients are closely related to illumination variation, and high frequency coefficients show detail and fine information that have possibly been caused by noise. The coefficients located between the first and the last coefficients present different information levels for the original image [25].
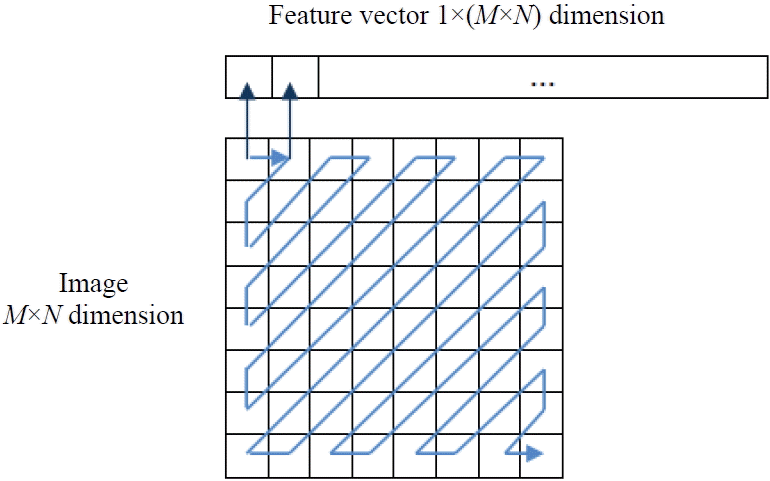
For the JPEG compression standard, the image is initially partitioned into no overlapping blocks (8×8 blocks), and the DCT is performed independently on the sub-image blocks [24]. However, in our approach, the DCT is computed on the entire representation of the face image and the DCT coefficients are arranged in a zigzag scanning manner, in order to map the M×N dimension image to the 1×(N×M) dimension vector and group low frequency coefficients at the top of the vector (see Fig. 7).
Since our purpose is to get age-invariant features, we know the following:
– Usually, facial aging consists of facial shape and skin texture variations.
– The appearance of a surface texture depends on illumination; thus, it changes under different illumination conditions.
– Illumination variations lie in the low frequency band.
– Generally, to recognize a person, we look for the principal characteristics of the face, such as the shapes and geometrical relationships of the main components of the face, including the eyes, nose and mouth, and we almost ignore some details related skin texture.
– As an example, the first row (a) in Fig. 8 displays four face images of the same person at different ages (24, 31, 42, and 61 years old) after normalization. The second row (b) in Fig. 8 shows reconstructed images of the same person after applying the DCT, taking a small set of low frequency coefficients, and applying the inverse DCT. The third row (c) in Fig. 8 shows reconstructed images of the same person after applying the DCT, setting a small set of low frequency coefficients to zero, and applying the inverse DCT. From the second and the third rows, we can see that reconstructed images discarding a set of low frequency coefficients present a diminution in some details (mainly, texture). However, the important features that characterize the face, such as the eyes, nose, etc., were preserved.
From these remarks, it can be concluded that the use of the DCT discarding some low frequency coefficients is crucial for successful feature extraction in face recognition across age progression.
3.5 Kernel Fisher Analysis
The Kernel Fisher Analysis, or the KFA method, is a kernelized version of linear discriminant analysis. It has been successfully applied to biometric recognition, such as palmprints [26] and face identification and verification [6,27,28].
In this approach, the input data is projected from the input space, ℛn, into an implicit high dimensional space, ℛf, known as a feature space, by a nonlinear kernel mapping function: Φ: ℛn, → ℛf, f > n, and then, the Fisher Linear Discriminant Analysis is adopted to this feature space. Using the same terminology and algorithm to perform KFA as in [6].
Assuming that projected samples Φ(xi) are centered in ℛf with the information of all samples and their classes, the between-class scatter matrix
where li is the number of samples in class i, c is the number of classes, and
To apply LDA in a kernel space, we need to find the eigenvalues λ and eigenvectors WΦ of:
which can obtained by finding a set of vectors
where, {
Consider c to be the number of classes and let the rth sample of a class t and the sth sample of a class u be Xtr and Xus, respectively, and the class t has lt samples and the class u has lu samples. The kernel function is then defined as:
Let K be a m×m symmetric matrix defined by the elements
Let Z be a m×m block diagonal matrix and each block (Zt) be a lt×lt matrix with terms all equal to
Any solution WΦ ∈ ℛf must lie in the span of all training samples in ℛf. For example:
It follows that the solution for (17) can be obtained by solving:
Therefore, Eq. (13) can be written as:
To avoid singularity in computing
4. Experimentation
4.1 Experimentation Methodology Description
All algorithms and normalization steps were implemented in MATLAB (R.2012a). To evaluate our method, we used the entire FG-NET database. It included 1,002 images divided into 82 classes (ranging in age from 0 to 69), for which there were a different number of images per class, and these numbers varied from 4 to 12. The database was used for face verification or face identification experiments to verify and test the invariance of the proposed approach.
For easy comparison with other results obtained on the FG-NET database, we adopted the same leave-one- person-out (LOPO) evaluation scheme adopted by [8,18,19], since this is the evaluation scheme used most often for the FG-NET database to divide the database into training and testing sets. This strategy selected all of the images of one person for testing and used all remaining images as a training set. This was repeated for all of the persons in the database. Thus, in the case of the FG-NET database the experiment was done 82 times. Hence, all images of one person were either in the training or the testing set. This strategy was adopted in order to ensure that the training and the testing sets were separated.
As we have already mentioned, there is a large variation in expressions, poses, and illumination between images in the FG-NET database. To evaluate our method, all of the images were preprocessed using the steps already presented in Section 3.2. Then, we transformed all of the images in a frequency domain using the DCT, we ordered the coefficient results in zigzag order, and we set a subset of the first low frequency coefficients to zero. Then, without doing inverse DCT, we applied a KFA to the results for dimensionality reduction, we used the polynomial kernel in our experiments, and we empirically chose the corresponding parameter of the kernel (Polynomial degree). Lastly, recognition was carried out by using a K-nearest neighbor classification, where K was selected equal to one (K=1) to calculate the Rank-1 recognition rates.
4.2 Results
The results of our experiments can be shown in two ways:
Table showing the identification rate at rank one (Rank-1 recognition rate) in the identification case and the equal error rate (EER) in the verification case. The results are the average of the 82 results we obtained from experiments using the LOPO strategy.
Cumulative match characteristic (CMC) curve [30] to show the recognition rate for ranks one and higher.
The performance measures were calculated by using the MATLAB PhD (Pretty Helpful Development) toolbox for face recognition [31,32].
We performed three experimentations to evaluate the performance of our proposed method. In all of the experiments extraction features were followed by a subspace KFA for dimension reduction.
In the first experiment, we studied the effect of using the AAM pose correction method, and we compared the obtained results using the AAM pose correction with those obtained using the approach described below.
Images were first rotated to get the eyes at fixed points so that the inter-ocular segment was horizontal based on files of eye coordinates that were provided with the original FG-NET database. The images were then cropped (using the eyes coordinates) to remove the background and were resized to 128×128. This approach is referred to in the following as manual alignment (MA). The results achieved clearly indicate the benefit of using the AAM as a pose correction method, where there is an improvement of 19.15% for the identification rate and a decrease in EER from 22.68% to 7.2% for verification in the case where we used the DCT. There was also an improvement of 23.14% for the identification rate and a decrease in EER from 37.70% to 17.23% without using DCT.
In the second experiment, we studied the importance of using the DCT. First, we compared the obtained results by applying the DCT on manually aligned images with those without the DCT. Second, we compared the results by combining the AAM and DCT with those using only the AAM. From the results achieved in these two cases we observed that adding the DCT increased the recognition rate by 14.22% and decreased the EER by 15.02% for verification in the first case. For the second case, the recognition rate was increased by 10.23% and the EER was decreased by 10.03% for verification. This led to the conclusion that using the DCT provides useful information for overcoming the variances in a face recognition system that are caused by variations in age.
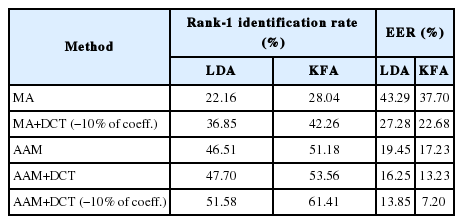
In the third experiment, we evaluated the performance of the DCT in the presence of age variations. We compared the results obtained by using the DCT on preprocessed images and set a few number of first coefficients to zero with those obtained without discarding coefficients. From Table 1 we can observe that applying DCT and discarding some coefficients achieved a rate of 61.41% in the case of identification and an EER of 7.2% in the case of verification. This had a 7.85% improvement for identification and 6.03% for verification, which demonstrates the impact of low frequency coefficients on the performance of face recognition in the presence of age variations.
To select the best percentage of low frequency coefficients to be discarded, we performed a succession of experiments. In each one we set a percentage of low frequency coefficients (0%, 5%, 10%, 15%, ..., 90%) to zero. The best recognition rate was between 10% and 15% (see Fig. 9). The recognition rate decreased when we chose high percentages, as seen in the last experiment where the obtained recognition rate was 0.6%. Obviously, there was a significant loss of information, which can be seen in Fig. 10. Fig. 10(a) represents the original image, Fig. 10(b)–(e) represent, respectively, reconstructed images after discarding 5%, 10%, 30%, and 85% of the low frequency coefficients. The last image Fig. 10(e) barely contains any information.

Normalized image of a person and its reconstructed images by setting to zero a percentage of low frequency coefficients.
Additionally, we demonstrated the importance of using the kernel method for dimensionality reduction. For this purpose we repeated the three experiments by using a Linear Fisher Analysis instead of the KFA. As seen in the results (see Table 1), the obtained rates with KFA are always higher than those obtained by using LDA.
From the results presented in Table 1, we notice that for temporal change tasks, the DCT discards some low frequency coefficients when coupled with the AAM normalization, and the KFA projection method still produced the best performances out of all of the cases studied.
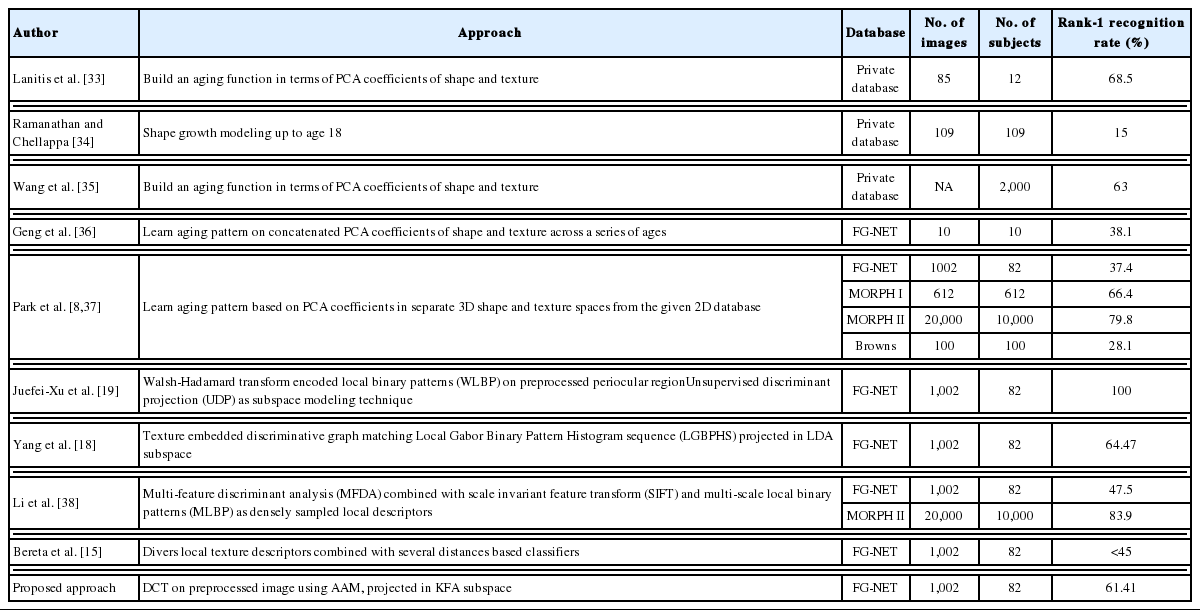
In Table 2, we summarize the results achieved by some approaches that have been proposed in the field of age-invariant face recognition and compared their results with ours.
From the results presented in Fig. 11, it is seen that our proposed approach provides the best result at rank-1 and always still the only best one at higher ranks. The importance of the preprocessed step, where always the combinations in which we use the AAM method (red, magenta and blue curve in Fig. 11) give the highest results, can also be seen.
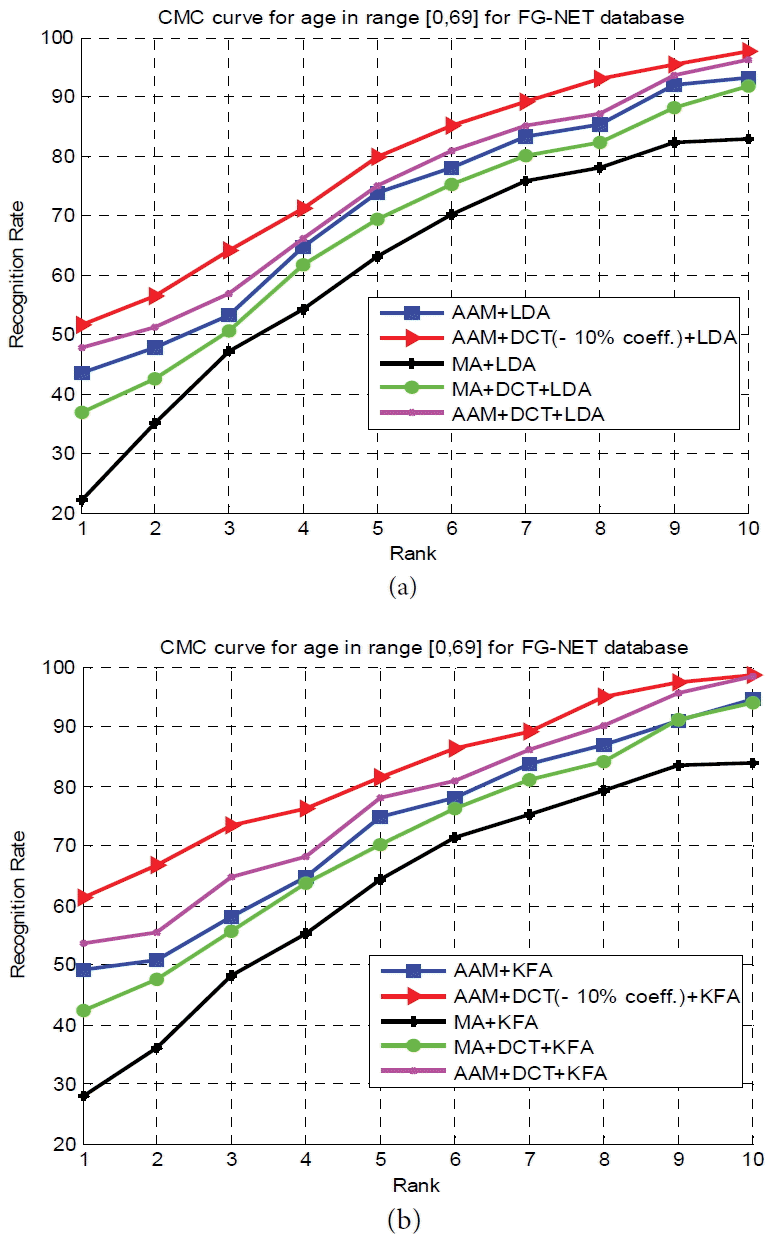
Cumulative match characteristic (CMC) curve for experiments on FG-NET database. (a) CMC curve by using Linear Discriminant Analysis (LDA) and (b) CMC curve by using Kernel Fisher Analysis (KFA).
It is worth noting that better results can probably be achieved if a component-based approach is used. The same process was applied for each component of the face (eyes, nose, and mouth) separately.
5. Conclusions
In this paper, we have presented an age-invariant feature extraction method for face identification and verification across age variations that consists of preprocessing steps that use the AAM, combined with the DCT, and followed by the KFA projection method. The proposed method provided a 61.41% Rank-1 identification and 7.2% EER for verification. The obtained results from experiments on the FG-NET database encourage the use of a combination of the AAM and DCT for face recognition across age progression. In the future, we will test our method on the MORPH database, study its robustness over large time lapses, and compare the obtained results with those obtained using other classifiers, such as SVM.
References
Biography
Leila Boussaad

She received the Dipl. Ing. degree in Computer Science in 1999 and the M.Sc. degree in computer science in 2009, both from Batna University, Algeria. She is now a PhD candidate in computer science at the same university. Currently, she works as an assistant professor in the department of Economics at Batna university, Algeria. Her research interests include Content-Based Image Retrieval, Biometry, and Pattern Recognition.
Mohamed Benmohammed

He is a professor in computer science at university of Constantine 2, Algeria. He received the Ph.D. degree from university of Sidi Bel-Abbes, Algeria, in 1997. His research interests include: Microprocessor, Computer Architecture, Embedded system and Computer Networks.
Redha Benzid

He received the Dipl. Ing. degree in electronics in 1994, the M.Sc. degree in electronics in 1999, and the Ph.D. degree in electronics in 2005, all obtained from Batna University, Algeria. Currently, he is a full Professor in the Department of Electronics at Batna University, Algeria. He co-authored several papers in refereed international journals and served as reviewer in Biomedical Signal Processing and control, IET Electronics letters, Digital Signal Processing and many other journals. His research interests include: Data Compression, Biomedical Engineering, Biometry, Digital Watermarking and Visual Cryptography.