Image Deblocking Scheme for JPEG Compressed Images Using an Adaptive-Weighted Bilateral Filter
Article information
Abstract
Due to the block-based discrete cosine transform (BDCT), JPEG compressed images usually exhibit blocking artifacts. When the bit rates are very low, blocking artifacts will seriously affect the image’s visual quality. A bilateral filter has the features for edge-preserving when it smooths images, so we propose an adaptive-weighted bilateral filter based on the features. In this paper, an image-deblocking scheme using this kind of adaptive-weighted bilateral filter is proposed to remove and reduce blocking artifacts. Two parameters of the proposed adaptive-weighted bilateral filter are adaptive-weighted so that it can avoid over-blurring unsmooth regions while eliminating blocking artifacts in smooth regions. This is achieved in two aspects: by using local entropy to control the level of filtering of each single pixel point within the image, and by using an improved blind image quality assessment (BIQA) to control the strength of filtering different images whose blocking artifacts are different. It is proved by our experimental results that our proposed image-deblocking scheme provides good performance on eliminating blocking artifacts and can avoid the over-blurring of unsmooth regions.
1. Introduction
Block-based discrete cosine transform (BDCT) coding has been widely adopted by the current mainstream image/video compression standards and technologies because of its excellent properties of energy compaction and decorrelation. For example, JPEG [1] and H.265/HEVC [2] are the most common international standards for still images and video compression, respectively. In an image compression based on BDCT, the image degradation would become visible when the compression ratio exceeds certain levels. It leads to the discontinuity of intensities between adjacent blocks due to the fact that images are segmented into rigid blocks and the correlations between blocks are neglected, namely blocking artifacts. In particular, the BDCT coding images will exhibit severe blocking artifacts when the bit rates are very low. Additionally, image-blocking artifacts not only become visually annoying, but also have a substantial effect on further image processing. Therefore, image deblocking is necessary for highly compressed images.
In order to reduce the shortcomings of BDCT, many researchers have proposed numerous algorithms. The algorithm that processes images only at the decoder side is called a post-processing algorithm. A post-processing algorithm is more practical because it does not affect the protocol contents of the encoder side and the protocol doesn’t need to be changed. These algorithms mainly include spatial filtering [3], transform domain filtering [4], projection iterative method [5], and so on.
To interact with the outside world effectively and rapidly, the human vision system (HVS) must extract and process a large variety of visual information from the captured images. Rather than adopting a uniform method to process these extracted structures from the captured images, HVS should be able to adapt to the different characters of these different extracted structures. Therefore, the maximum amount of information can be extracted from the extracted structures for the subsequent recognition stage and for image processing. It is this point that an adaptive and effective image processing system should be designed in order to make the machines have the adaptive capabilities of biological vision systems. A lot of works and researches have been done for adaptive image deblocking. For suppressing blocking artifacts and preserving image salient features, Foi et al. [6] proposed an adaptive image filtering method using the shape-adaptive DCT (SA-DCT), which empirical Wiener filtering and hard-thresholding technology were adopted in the SA-DCT domain. In addition, Zhai et al. [7] proposed one kind of a comprehensive image-deblocking algorithm, including three processing stages. In the second stages, block-wise shape adaptive filtering was proposed to further ameliorate edge features. To avoid possible over-smoothing, a quantization constraint set is also adopted in the third stage. Furthermore, the proposed method has relatively low computational complexity. According to the process analysis of image coding and the characteristics of a BDCT compressed image, we can formulate image deblocking clearly as optimization problems that solve the objective function using a set of convex functions [8]. Wang et al. [9] proposed an adaptive spatial post-processing method that is composed of three steps: thresholding, model classification, and a deblocking filter. Compared with these proposed adaptive image-deblocking methods, the most straightforward way is to conduct low pass filtering around the block boundaries. However, low pass filtering filters out some high frequency information, which leads to image over-smoothing and blurring. To make images obtained by the optical coherence tomography valuable for clinical interpretation, Anantrasirichai et al. [10] proposed an adaptive-weighted bilateral filter. The novel filter not only offers the desirable property of removing speckles, but also preserves texture and useful information contained in the optical coherence tomography images. Hu et al. [11] designed one kind of adaptive depth map filter based on a bilateral filter for image deblocking. The parameter of this proposed adaptive depth map filter is changed adaptively according to image edges and blocking artifacts.
In this paper, an original image deblocking method using an adaptive-weighted bilateral filter is proposed. This novel adaptive-weighted bilateral filter is proposed based on local entropy and improved blind image quality assessment for the sake of eliminating blocking artifacts and avoiding over-smoothing. The rest of this paper is organized as follows: We briefly introduce the related works in Section 2. In Section 3, we present the proposed adaptive-weighted deblocking filter algorithms. In Section 4, experimental results and comparisons are presented. Finally, we give our conclusion and further research in Section 5.
2. Related Works
2.1 Bilateral Filter
The bilateral filter [12] is a tool that can smooth images while preserving image edges and texture regions. The principle of a bilateral filter is analogous to the Gaussian convolution, which is defined as the weighted average of pixel values. The difference between a Gaussian filter and bilateral filter is that the bilateral filter takes into account not only the spatial locations but also the intensity variation to preserve image edges. The principle of bilateral filtering is that two pixels in images are analogous to each other based on spatial locations and similarity in the photometric range. A new weighted average of pixel p can be obtained by Eq. (1):
where, S is the window space. Gσd (·) and Gσr (·) are the closeness and the similarity functions that are the Gaussian functions with the standard deviations of σd and σr, respectively. ||·||represents the Euclidean distance, and ωp is used for normalization.
The performance of a bilateral filter is controlled by two parameters of σd and σr. σd is important in image spatial domain processing because it determines the level of low-pass filtering. A greater value of σd will combine and weigh more pixels in the neighborhood together, which leads to a greater blurring effect. σr determines the weights in an image intensity domain. According to the value of σr, pixel points in the window space S where their values are closer to each other are combined and weighted together. Examples of smoothing images by the bilateral filter with fixed parameters are shown in Fig. 1. The bilateral filter with fixed parameters cannot obtain good results in removing the blocking artifacts.
2.2 Local Entropy
According to Shannon’s definition of entropy, the image entropy is defined as Eq. (2):
where, i is grayscale and L is the maximal grayscale.
where, j is the grayscale.
For the small neighborhood Ωk, the local entropy E(Ωk) is closely correlated with the variance of grayscales. From Eq. (3), the local entropy is smaller in homogeneous regions and larger in inhomogeneous regions. Hence, the pixel points in smooth regions will have smaller local entropy values than those in unsmooth (edge and texture) regions of the image. If we select an appropriate neighbor window Ω for the image, the local entropy of the image would be computed. When the neighbor window Ω is moved on a per-pixel basis within the image from top to bottom and from left to right, the local entropy value of each pixel point will be obtained, that is, we can obtain a local entropy image. Fig. 2 is the local entropy map of Lena. From Fig. 2, we can see that the edge and texture regions can be clearly distinguished from the smooth regions.
3. The Proposed Scheme Using an Adaptive-Weighted Bilateral Filter
To improve the quality of JPEG compressed images, we need to protect edge and texture information when the image is to be deblocked. In other words, σr and σd must be larger to remove blocking artifacts in smooth regions. For regions with more significant details, σr and σd should be smaller to avoid blurring details. Although a bilateral filter can protect image edges while smoothing the image, the filter with fixed parameters cannot work well because it may lead to the loss of some texture information, as shown in Fig. 1. Local entropy can show the discrete degree of image grayscales. For smooth regions of the image, the local entropy is smaller. In texture and edge regions, the local entropy is larger. As such, this paper proposes a novel adaptive-weighted bilateral filter using the local entropy map g(x) as the guidance image to obtain adaptive parameters.
σr is calculated for a pixel located at x:
where, nr is a minimum level of filtering to avoid σr = 0. gmax is the maximum value of g(x), and kr is a constant parameter that controls the mapping process of g(x) to σr.
σd is calculated for a pixel located at x:
where, nd is a minimum level of filtering to avoid σd = 0, and kd is a constant parameter that controls the mapping process of g(x) to σd. The parameters kr and kd are similar to σr and σd, which determine the performance of the bilateral filter. The framework of our proposed adaptive-weighted filter is shown in Fig. 3.
For images whose blocking artifacts are more serious, we need to select larger parameters ( kr and kd ) to smooth images as much as possible. For images with slight blocking artifacts, we should select smaller parameters ( kr and kd ) to avoid over-smoothing images. In this paper, we adopted three sets of data for kr and kd according to the severity of image blocking artifacts.
In general, it is not possible to obtain the original image on the decoder side. In this paper, we adopted and improved a kind of blind image quality assessment (BIQA) as criterion according to [13] to choose appropriate parameters ( kr and kd ) for different decoded images. For the test image signal x(m, n) with m ∈ [1, M] and n ∈ [1, N], and a differencing signal on each horizontal line can be calculated as:
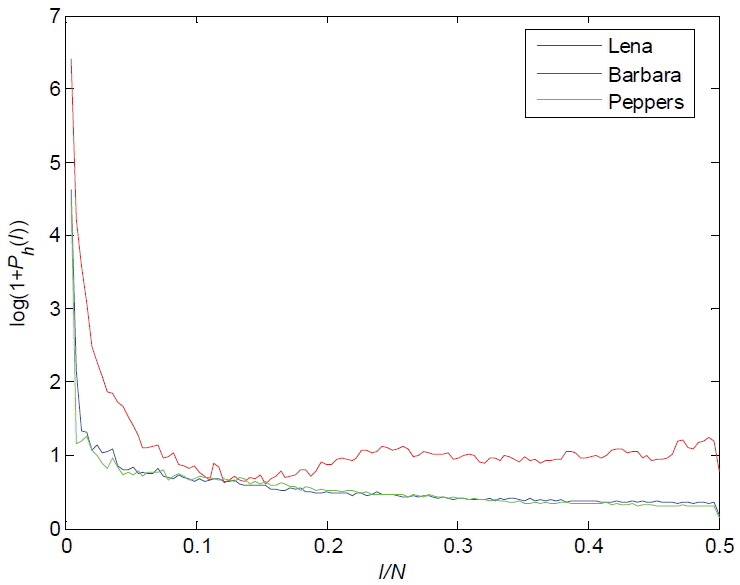
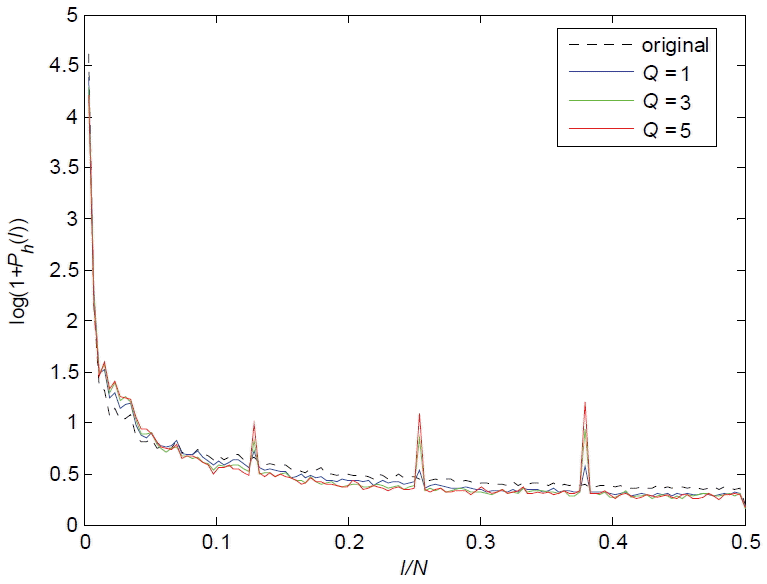
For a 1-D horizontal signal fm(n) = |dh(m, n)|, we first calculated its power spectrum for m = 1,2, …, M and then averaged them together. Finally, the power spectrum estimation Ph(l), 0 ≤ l ≤ 2/N can be obtained, which is exemplified in Fig. 4. As shown in Fig. 4, the different original images have similar power spectrum. When we adopted different quantization factors (Q = 1, Q = 3, and Q = 5), the image blocking artifacts can be easily picked out based on the peaks at the feature frequencies (1/8, 2/8, 3/8, and 4/8), as shown in Fig. 5. In addition, if the image is compressed more highly, the peaks will change more significantly. According to the characteristics of the image power spectrum, the criterion to select the parameters ( kr and kd ) is to calculate S. This is defined as:
The image quality scores S of three images, which are calculated by Eqs. (7)–(10), are shown in Fig. 6. The three images are Lena, Barbara, and Peppers. All of them are compressed by JPEG where the quantization factor Q varies from 1 to 10. From Fig. 6, we can see that if the quality of image is bad, S is large. The flow diagram of our proposed image-deblocking scheme is shown in Fig. 7. If S was smaller than α, then we selected (krs, kds) for (kr, kd); if S was larger than α and smaller than β, then (krm, kdm) was used; and if S was larger than β, (krl, kdl) was used. The parameters (krs, kds), (krm, kdm), and (krl, kdl) were determined empirically and set as follows: (krs, kds) = (1,10), (krm, kdm) = (3,20), and (krl, kdl) = (5,30).

The image quality scores of Lena, Barbara, and Peppers images using quantization factor Q from 1 to 10.
In order to determine the threshold values α and β (α<β), we selected three images: Lean, Barbara, and Peppers. They were compressed by JPEG where the quantization factor Q varied from 1 to 10. All of them were carried out according to the steps shown below, which are also shown in Fig. 8:
The first decoded image of the Lena (Barbara or Peppers) image is processed by the proposed adaptive-weighted bilateral filter in which the parameters of (kr, kd) are (krs, kds) and (krm, kdm), respectively. The obtained images are called output image1 and output image. Their scores are calculated using the proposed method, namely Ss and Sm. If S s < S m, then S0, which is the quality score of the compressed image, is the threshold value α. If S s > Sm, continue to step (ii). This step is shown in the black box and solid line.
The decoded image is processed by the proposed adaptive-weighted bilateral filter in which the parameters of (kr, kd) are (krl, kdl), and we calculated the scores of the obtained image called output image2, namely Sl. If Sl < Sm, S0 is the threshold value β. If Sl > Sm, S0 is larger than α and smaller than β. This step is shown in the blue box and dotted line.
The other images of Lena use the same steps to modify α and β.
In this paper, the best value ranges of α and β for the Lena, Barbara, and Peppers images are shown in Table 1. According to Table 1, we selected α = 0.3000 and β = 0.9500.
4. Experimental Results
To test the performance of our proposed scheme, a lot of experiments have been conducted on monochrome and color images. In this paper, the images with blocking artifacts were obtained by JPEG. For monochrome images, we used three digital images—Lena, Barbara, and Peppers—to test the effectiveness and efficiency of our proposed scheme. For color images, we adopted images from the LIVE database. The method of bilateral filtering with fixed parameters and the method proposed in [11] were performed. These results were compared with the results from using our proposed algorithm to test the performance of our proposed method. The simulation was conducted with MATLAB 2009a. Here, we computed the PSNR and SSIM between the deblocked image and the uncompressed image. PSNR is defined as shown in Eq. (11):
where, MSE is the mean squared error between the deblocked image and the uncompressed image. And SSIM is defined as shown in Eq. (12):
where, μx and μy are the average of the deblocked image x and the uncompressed image y, respectively, and
In terms of PSNR and SSIM, Tables 2–4 show the experimental results of our proposed scheme compared to other methods applied to the Lena, Barbara, and Peppers images at various bit rates, respectively.
From Tables 2–4, we can see that our proposed algorithm has excellent performance compared with the two mentioned methods. Our proposed scheme can provide the best results. For these images, the results are improved from a minimum of 0.20 dB up to 1.00 dB in terms of PSNR, and the SSIM is also improved compared with the compressed images. When these images are at very low bit rates, the method proposed in [11] and the method of bilateral filtering with fixed parameters can improve their quality. However, when the images are not at very low bit rates, they cannot improve the quality and may actually reduce it. The reasons for this are that the method presented in [11] only changes one parameter and the method of bilateral filtering with a fixed parameter uses a fixed parameter.
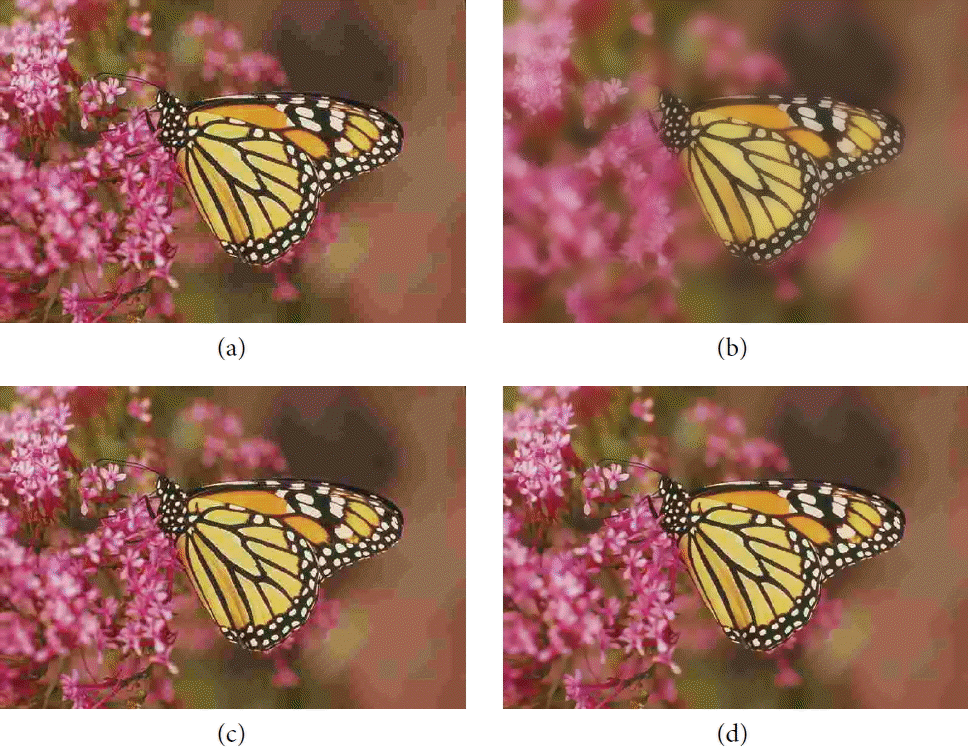
Fig. 9 shows the perceived image quality for the Monarch image at a 0.3211 DMOS score. From Fig. 9, we can see that if we used the bilateral filter with fixed parameters, the image would be over-smoothed, as shown in Fig. 9(b). If we only change one parameter of the bilateral filter (method in [11]), there is still blackness in the wings for the Monarch image, as shown in Fig. 9(c). Our method can achieve better effects for image deblocking.
5. Conclusions
A new efficient image blocking scheme based on adaptive-weighted bilateral is proposed in this paper. We used a local entropy map as a guidance map to change two parameters (σr and σd ) in a bilateral filter. In this process, we also proposed one criterion to determine kr and kd, because blocking artifacts of different images after compression are different. Through these two steps, we were able to obtain good results in terms of PSNR and SSIM.
Our experimental results show that the proposed scheme can reduce the blocking artifacts at low bit rates. In this paper, we did not consider the optimal selection for the BIQA. Furthermore, good improvements can be obtained by considering human visual characteristics and GPU or the parallel method. In the future, we may focus on these issues.
Acknowledgement
This work was supported by the National Natural Science Foundation of China (No. 61201371), the Natural Science Foundation of Shandong Province, China (No. ZR2015PF004), and the promotive research fund for excellent young and middle-aged scientists of Shandong Province, China (No. BS2013DX022). The authors thank Qiming Fu, Yunpeng Zhang, and Heng Zhang for their generous assistance and valuable suggestions.
References
Biography
Liping Wang http://orcid.org/0000-0003-0686-3862

She was born in Shandong province, China, in 1990. She received her B.E. degree in communication engineering from Shandong University, Weihai, China, in 2014. She is currently pursuing her M.E. degree in signal and information processing at Shandong University, China. Her current research interests include digital image processing and computer vision.
Chengyou Wang http://orcid.org/0000-0002-0901-2492

He was born in Shandong province, China, in 1979. He received his B.E. degree in electronic information science and technology from Yantai University, China, in 2004, and his M.E. and Ph.D. degrees in signal and information processing from Tianjin University, China, in 2007 and 2010, respectively. He is currently an associate professor and supervisor of postgraduate students at Shandong University, Weihai, China. His current research interests include digital image/video processing and analysis (transform coding, digital watermarking, image dehazing, image quality assessment, etc.), computer vision (tamper detection, image retrieval, etc.), and pattern recognition and machine learning.
Wei Huang

He was born in Inner Mongolia autonomous region, China, in 1990. He received his B.E. degree in electronic information science and technology from Wuhan University, China, in 2014. He is currently pursuing his M.E. degree in communication and information system at Wuhan University, China. His current research interests include wireless communication technology and digital image processing.
Xiao Zhou http://orcid.org/0000-0002-1331-7379

She was born in Shandong province, China, in 1982. She received her B.E. degree in automation from Nanjing University of Posts and Telecommunications, China, in 2003; her M.E. degree in information and communication engineering from Inha University, Korea, in 2005; and her Ph.D. degree in information and communication engineering from Tsinghua University, China, in 2013. She is currently a lecturer and supervisor of postgraduate students at Shandong University, Weihai, China. Her current research interests include wireless communication technology, digital image processing, and computer vision.