A Novel DWT-SVD Canny-Based Watermarking Using a Modified Torus Technique
Article information
Abstract
Today’s modern world requires a digital watermarking technique that takes the redundancy of an image into consideration for embedding a watermark. The novel algorithm used in this paper takes into consideration the redundancies of spatial domain and wavelet domain for embedding a watermark. Also, the cryptography-based secret key makes the algorithm difficult to hack and help protect ownership. Watermarking is blind, as it does not require the original image. Few coefficient matrices and secret keys are essential to retrieve the original watermark, which makes it redundant to various intentional attacks. The proposed technique resolves the challenge of optimizing transparency and robustness using a Canny-based edge detector technique. Improvements in the transparency of the cover image can be seen in the computed PSNR value, which is 44.20 dB.
1. Introduction
Digital watermarking is the technique of embedding additional data, which is defined as, watermark into the original data so that the original information remains secure despite external attacks on it. This helps in applications like copyright protection, data authentication, data authorization, piracy prevention, etc.
The digital world is prone to various external forces that may purposely or mistakenly affect the embedded information and make it void. The basic challenge for designing a digital watermarking system is to recover the embedded information despite various attacks on the data. In order to attain this objective, various attacks were performed on the system and the overall response of the system was evaluated.
The basic challenges while designing a watermarking technique are transparency and robustness, which conflict with one another. Also, the domain, in which embedding is done, is of utmost importance as spatial domain methods are prone to various attacks. So, we have proposed a technique that is flexible in dealing with spatial differences and maintaining robustness and transparency.
2. Related Work
The technique of Lai and Tsai [1] embeds a watermark in the singular values of the cover image’s discrete wavelet transform (DWT) sub-bands. The technique fully exploits the spatio-frequency localization of the DWT of these two transform domain methods, and the singular value decomposition (SVD) efficiently represents the intrinsic algebraic properties of an image [1]. Liu and Tan [2]’s technique embeds the watermark in singular values of the cover image directly. Properties of SVD lead to the good performance of the novel algorithm in both security and robustness. Principle component analysis is used to uncorrelate the R, G, and B channels of both of the images, and the technique of DWT-SVD is extended for color images [3].
Kumari et al. [4] used the hierarchical approach and torus automorphism to gain high security over other methods and to increase robustness for common attacks. Elazhary [5] proposed a watermarking technique based on extended torus automorphism, which enhances the security of torus automorphism by adding cryptographic elements to the transform. Ganic and Eskicioglu [6]’s method is based on DWT-SVD, but the data is embedded on different frequencies. Hernandez et al. [7] measured the performance for the DCT domain-based watermarking technique. DWT is widely used in watermark embedding due to its various advantages over other transforms [8–10]. Modern Techniques like digital signatures, Multiresolution watermarking and SVD based algebraic methods are added for improving security of watermarking methods [11–15]. These techniques exploit either frequency domain or spatial domain. This paper proposes a spatio-frequency domain, which makes the watermark more robust.
3. Proposed Technique
3.1 Watermark Embedding
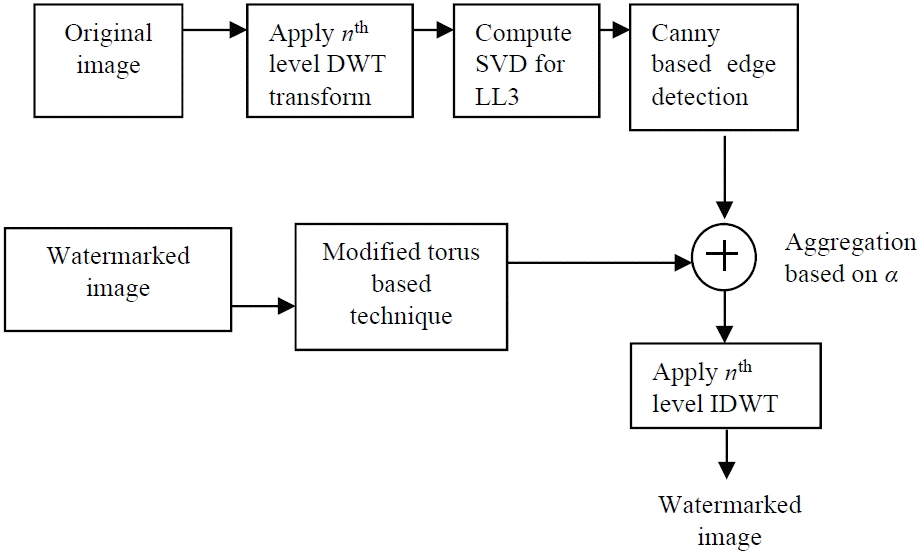
Our proposed technique, as shown in Fig. 1, works in the DWT domain and computes the nth level wavelet decomposition of the cover image. We used the 3rd level wavelet decomposition and computed the lower band frequency component LL3. Then, the SVD for a lower band frequency component gives the singular value matrix S, which is a diagonal matrix and has the information of the contents of the original signal. Mathematically, the SVD to the LL sub-band gives:
where U and V are orthogonal matrices and S is a singular matrix.
A canny-based edge detector detects the edges present in the singular matrix S. It helps in searching for redundancy in an image in a wavelet domain so that the value of the alpha can be varied, which results in the sharpening of edges. The variability of the value of the alpha gives optimality between robustness and transparency. Another variation is the modified Torus Transform, wherein the value of k and n are such that they are not co-primes. This ensures the invertibility of the transform and allows the resultant watermark to be recovered. The Torus Transform can be computed as:
where i, j are original matrix indices, i★, j★ are transformed matrix indices, and k and n are transform parameters used for decoding the watermark.
The values of k and n are essential in order to recover the original watermark. These values serve as the secret keys for watermark recovery. A modified torus transform is applied on the watermark to produce a permuted watermark, which can only be unlocked using the secret key known to the owner.
The singular value of the watermark image Sw can be computed by varying α and using the cover image singular values of Sk to obtain a new singular matrix Skn as:
The DWT transformed watermarked image Swh is obtained using a convolution as:
where Uk and Vk are the orthogonal matrices of the cover image.
Finally, the inverse DWT gives the watermarked image, which is similar to the cover image and has watermark information embedded in it.
3.2 Watermark Extraction
This technique is referred to as “blind,” as it does not require an original cover image in order to extract the watermark. Secret keys, orthogonal matrices of the watermark, and the singular value matrix of the original image are required to retrieve the original watermark. The watermarked image is decomposed using the nth level DWT. In our proposed technique, the 3rd level DWT was applied to the watermarked image, and a canny-based edge detection technique was used to determine the value of α. The resultant is then added using the watermarked image singular values. Mathematically, this can be shown as:
where Snew is the new watermarked image singular value, Sk is the singular value matrix of the cover image, and Sw is the singular value matrix of the watermarked image.
The lower band frequency component, LL3, of the watermarked image is obtained as Snew and the orthogonal matrices of the original watermark both on convolution give the permuted version of original watermark Aw:
The inverse torus transform, as shown in Fig. 2, extracts the original watermark.
4. Results
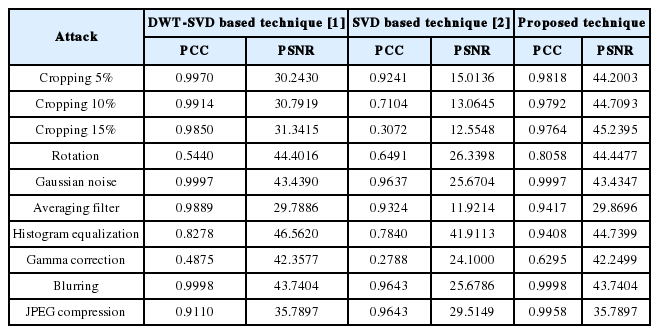
In order to check the robustness and transparency of the proposed technique, various attacks, including cropping, rotation, Gaussian noise, average filtering, histogram equalization, gamma correction, blurring, and JPEG compression, were performed on the watermarked image. We computed the peak signal-to-noise ratio (PSNR) for measuring the transparency of the image, which is significantly improved compared to the DWT-SVD-based technique. Also, the Pearson correlation coefficient (PCC) was used to measure the robustness of the algorithm by measuring the similarity between the original watermark and the recovered watermark, as shown in Table 1.
The Lena image (512×512) was used as the cover image and Cameraman (64×64) was used as the watermark. For a cover image that was 1024×1024 or bigger and the same PSNR watermark were also improved. The cover image, watermark, and watermarked image are shown in Fig. 3. Watermarks that were recovered after various attacks are shown in Fig. 4.

Watermark recovered after various attacks: (a) cropping, (b) rotation, (c) Gaussian noise, (d) average filtering, (e) histogram equalization, (f) gamma correction, (g) blurring, and (h) JPEG compression.
As shown in Table 1, there is a dilemma between transparency and robustness. SVD-based techniques are robust, but are the least transparent; whereas, DWT-SVD based techniques are robust and less transparent. Our proposed technique achieves good robustness for rotation, histogram equalization, gamma correction, and JPEG compression attacks. Also, our proposed technique is the most transparent, which can be seen in the computed PSNR. (a) (b) (c)
5. Conclusions
Our proposed technique takes into consideration spatial domain and frequency domain redundancies to embed a watermark, which makes it more robust and transparent. A wavelet transform helps to embed the coefficients of the watermark at various resolutions, and a canny detector ensures the edges to compute the value of α depending on the human visual system. Also, the modified torus transform ensures robustness against cropping attacks, and the secret key ensures ownership protection.
References
Biography
Salima Lalani

She was a gold medalist in the degrees of B.E. and M.E. in Computer Science and Engineering from Swami Ramanand Teerth Marathwada University in 2008 and 2011, respectively. Since November 2011, she is with the SGGSIE&T, Computer Science and Engineering Department from SRTM University as a PhD candidate.
D. D. Doye

He received B.E. and M.E. degrees in Electronics from Marathwada University Aurangabad in 1988 and 1993, respectively. He received Ph.D. in 2003 from Swami Ramanand Teerth Marathwada University, Nanded. Presently, working as Professor since 2003 in Department of Electronics and Telecommunication Engineering, SGGS Institute of Engineering and Technology, Nanded, India. His research field includes Speech processing, Image processing and Pattern recognition.