Sparsification of Digital Images Using Discrete Rajan Transform
Article information
Abstract
The exhaustive list of sparsification methods for a digital image suffers from achieving an adequate number of zero and near-zero coefficients. The method proposed in this paper, which is known as the Discrete Rajan Transform Sparsification, overcomes this inadequacy. An attempt has been made to compare the simulation results for benchmark images by various popular, existing techniques and analyzing from different aspects. With the help of Discrete Rajan Transform algorithm, both lossless and lossy sparse representations are obtained. We divided an image into 8×8-sized blocks and applied the Discrete Rajan Transform algorithm to it to get a more sparsified spectrum. The image was reconstructed from the transformed output of the Discrete Rajan Transform algorithm with an acceptable peak signal-to-noise ratio. The performance of the Discrete Rajan Transform in providing sparsity was compared with the results provided by the Discrete Fourier Transform, Discrete Cosine Transform, and the Discrete Wavelet Transform by means of the Degree of Sparsity. The simulation results proved that the Discrete Rajan Transform provides better sparsification when compared to other methods.
1. Introduction
Images are usually circulated amongst millions of users around the world via the Internet or through TV, etc., almost every 60 seconds. It is important to note that a huge bandwidth is required to transmit digital visual media [1]. This has led to the advent of the active research area of image compression [2,3]. Image compression is all about the reduction of the amount of data required to represent a digital image. There are three basic types of redundant information that can be noticed in digital data. They are: coding redundancy, spatial and temporal redundancy, and irrelevant information that is usually ignored by the human visual system. Compression can be achieved by removing one or more of the three basic data redundancies mentioned above. However, there has to be a trade-off between the acceptable level of errors in the reconstructed image and the original image [4]. It also has to be understood that images contain complex sets of data and that there are no existing transforms available in current studies that can be optimally and efficiently used to represent the content in the image.
That is, no technique can be used as a universal tool to represent all types of data in a compressed form. For example, consider an image with oscillatory texture; the Fourier transform performs better in terms of providing a sparse representation effectively. Similarly, the DWT provides a better performance if the image has isolated singular textures [2]. This fundamental concept paved the way for the development of many algorithms. There are many algorithms that are standard and widely used in the field of image compression. The JPEG2000 standard is the most popular among these techniques and it is based on the fundamental fact that the images have a certain sparsity associated with them when they are represented by wavelets [2,3].
Sparse representation of an N-dimensional vector X ∈ RN implies that any arbitrary signal could be represented by a relatively lower number of large non-zero coefficients [3]. If the K of the coefficients of the signal X are non-zeros and the rest of the (N-K) coefficients are either negligibly small or zero, then the signal is said to be K-sparse [5]. Sparsity in a signal implies that there is a relatively lower number of large non-zero coefficients and a greater number of zero or near-zero coefficients [2]. The compressibility of a signal is high if the maximum energy is distributed amongst the lower number of coefficients. In other words, it is apt to say that sparse signals are highly compressible [6]. Hence, a sparse representation has potential uses in image compression techniques, but a compromise has to be made with the entropy of the signal. Sparse signals can be reliably reconstructed by using the values and positions of large non-zero coefficients in a signal. This is called sparse approximation and it is the fundamental basis for transform coding [5].
In this paper, prospective applications of the Discrete Rajan Transform (DRT) in image sparsification have been considered. The application of DRT will be viewed from the perspective of making the input image sparse; thus making it more compressible, easier to process and store.
2. Transform-Based Sparsification of Image Data
The sparsification of a signal is defined as a process of making the most of the coefficients present in it are zero or nearly zero.
A finite N-dimensional vector can be called a sparse signal if most of the coefficients present in it are zero or nearly zero. If the K coefficients are non-zero and the remaining (N-K) number of elements within the data set is zero, then the signal vector can be called a K-sparse signal.
In other words, sparsification is a process of introducing zero elements in the given data be it a sequence or an array. It is common practice to go for sparsification in the time domain or spatial domain, according to if the data is time dependent or space dependent. Orthogonal transforms, such as Discrete Fourier Transform (DFT), Discrete Cosine Transform (DCT), and Discrete Wavelet Transform (DWT), are used to sparsify data in a time domain or spatial domain, whereas, DRT is used to sparsify 1-D and 2-D data in the respective spectral domains.
In a signal, the energy distribution determines the ‘degree of sparsity’ of that signal. If the distribution of energy is such that all of or the maximum amount of its energy is represented by one coefficient and all of the other coefficients are zero, then the signal representation can be considered as being the most sparse. This type of signal representation would be highly compressible. The least sparse signals have an even distribution of energy out of the coefficients present in them.
The degree of sparsity of a signal can be defined as “a ratio of the number of zero and nearly zero samples to the total number of samples present in the signal, multiplied by 100”. For example:
where, (N-K) represents the number of zero-valued and near zero-valued coefficients, N represents the total number of coefficients, and K represents the number of non-zero coefficients.
The degree of sparsity of a signal determines the number of non-zero coefficients among which the entire energy is distributed. The higher the degree of sparsity, the lower the number of non-zero coefficients is, among which the maximum energy is distributed. In other words, the higher the degree of sparsity, the higher the number of zero and nearly zero coefficients is. The advantages of a sparse signal are as follows:
Increased processing speed and reduction in the complexity.
Sparsity can be used to estimate efficient algorithms in terms of quality.
Sparse representation could result in better compression.
The precision of the transform coder is also influenced by the degree of sparsity.
Transforms used for sparsifying the signal are called Sparsifying Transforms. Generally, every image transform provides some sparsification. In this paper, it is proved that DRT provides better sparsification than that provided by DFT, DCT, and DWT.
In the existing literature, there are many widely used orthogonal transform basis functions that can help to obtain the sparse representation of image signals. The frequently used transforms are DFT, DCT, DWT, and DRT to name a few [7,8]. The basic principle of transforms is that they decompose signals over the basis functions, as per the algorithm, to analyze and understand the properties and behavior of input signals [9]. Considering the case of Fourier analysis, a finite energy function f(t) can be represented as a sum of sinusoidal and cosine functions ejωt. If the function f(t) is regular, decomposition is faster and easier. Sparse representations are possible through Fourier transform if the functions are uniform and regular in nature [10]. Another transform that has been chosen to obtain a sparsely represented signal is the DCT. In cases where analyzing signals that are of different sizes, it would be desirable to have knowledge about the time and frequency elements. The wavelet transform can help in measuring the time evolution of the frequency transients of the signal by separating the amplitude and phase components that are associated with it [9]. The wavelet transform can be used to decompose any signal over dilated and translated wavelets to obtain a sparsely represented signal. In the DWT, a wavelet is the orthogonal basis function that is used to decompose a finite set of signals. The Rajan Transform (RT) is a variant of the Hadamard Transform, which was initially developed for the purpose of pattern recognition. RT is permutation invariant and is homomorphic in nature. It is because of this property that RT has potential applications in pattern recognition algorithms like thinning, edge detection, contour detection, and the detection of curves and lines in images and the isolation of certain points in images [11]. Unlike RT, the generalized DRT has been moulded to exhibit isomorphism when the auxiliary phasor information associated with the spectrum is a known apriori. With the help of the DRT algorithm, both lossless and lossy sparse representation can be obtained.
The principle of DRT (i.e., the formulation of DRT) has been discussed by the authors in [12].
3. DRT as a Sparsifying Transform
The algebraic formulation of traditional transforms is conducive for temporal or spatial sparsification, whereas, the algebraic formulation of DRT is conducive for spectral domain sparsification. That is precisely why DRT is used for spectral domain sparsification and subsequent data compression. The non-linear property of DRT is the main reason for providing better sparsification than other transforms.
For a random input signal of length 256×1, different block lengths (in powers of 2) were considered. The total number of (N-K) sparse coefficients obtained was compared with different block lengths. Fig. 1 below shows the performance of DFT, DCT, DWT, and DRT in providing sparsity.

Performance of Discrete Fourier Transform (DFT), Discrete Wavelet Transform (DWT), Discrete Cosine Transform (DCT), and Discrete Rajan Transform (DRT) for random input signal. (a) Plot of amplitudes of transformed signal output of DFT, DCT, DRT and DWT. (b) Comparison of K sparse representation obtained from DFT, DCT, DRT and DWT.
From Fig. 1(b), it can be observed that for the input signal up to the block length 24, DWT provided better sparse representation compared to DFT, DCT, and DRT. Beyond that, DRT showed better performance. Out of the total 256×1 samples, beyond block length 24, DRT produced about 24% of the N-K sparse coefficients. For the block length 27, DRT produced an average of 98%. DFT and DCT, however, gave less than 1% N-K sparse coefficients. From Fig. 1(a), it can be observed that the maximum of DRT spectral coefficients are less than zero. Hence, it is possible to achieve further sparsification with DRT through the thresholding operation.
A similar analysis was carried out using an image input that was 512×512 in size. The performance of each of the candidate transforms is depicted in Fig. 2. For different input images, the transformed signal output obtained from the DRT showed that an average of approximately 23% of the spectrum was zero coefficients and that many of the remaining coefficients were nearly zero, thus exhibiting the possibility of achieving a better sparse output when compared to the other three candidate transforms chosen for this research.

Performance of Discrete Fourier Transform (DFT), Discrete Wavelet Transform (DWT), Discrete Cosine Transform (DCT), and Discrete Rajan Transform (DRT) for a 512×512 image input. (a) Plot of amplitudes of transformed signal output of DFT, DCT, DRT and DWT. (b) Comparison of K sparse representation obtained from DFT, DCT, DRT and DWT.
A special case of DRT was used where the auxiliary phasor information in each stage was considered to be 1. To obtain further sparse representation through DRT, a thresholding function can also be applied. Also, the sparsest representation can be obtained by just taking into account the Cumulative Point Index (CPI) value—the first spectral components—of each block in the transformed signal. However, both of the above-mentioned methods for obtaining better sparsity can be classed as lossy due to the loss of a significant amount of data.
Considering the lossy case, even the higher degree of sparsity can be obtained using CPI values and CPI, along with the mid-spectral component of the DRT transformed output at different block lengths. But, in this case, the compromise would be the loss of information in the signal [13].
DRT has potential applications in image processing and compression. In this paper, only the application of DRT to obtain the sparse representation of images is considered. Standard images have been considered and to make DRT processing easier, the image was divided into blocks that are 8 in size. The DRT was applied to it and the special case of DRT, as mentioned earlier, was considered. The results obtained are presented in the next section.
4. Proposed Algorithm
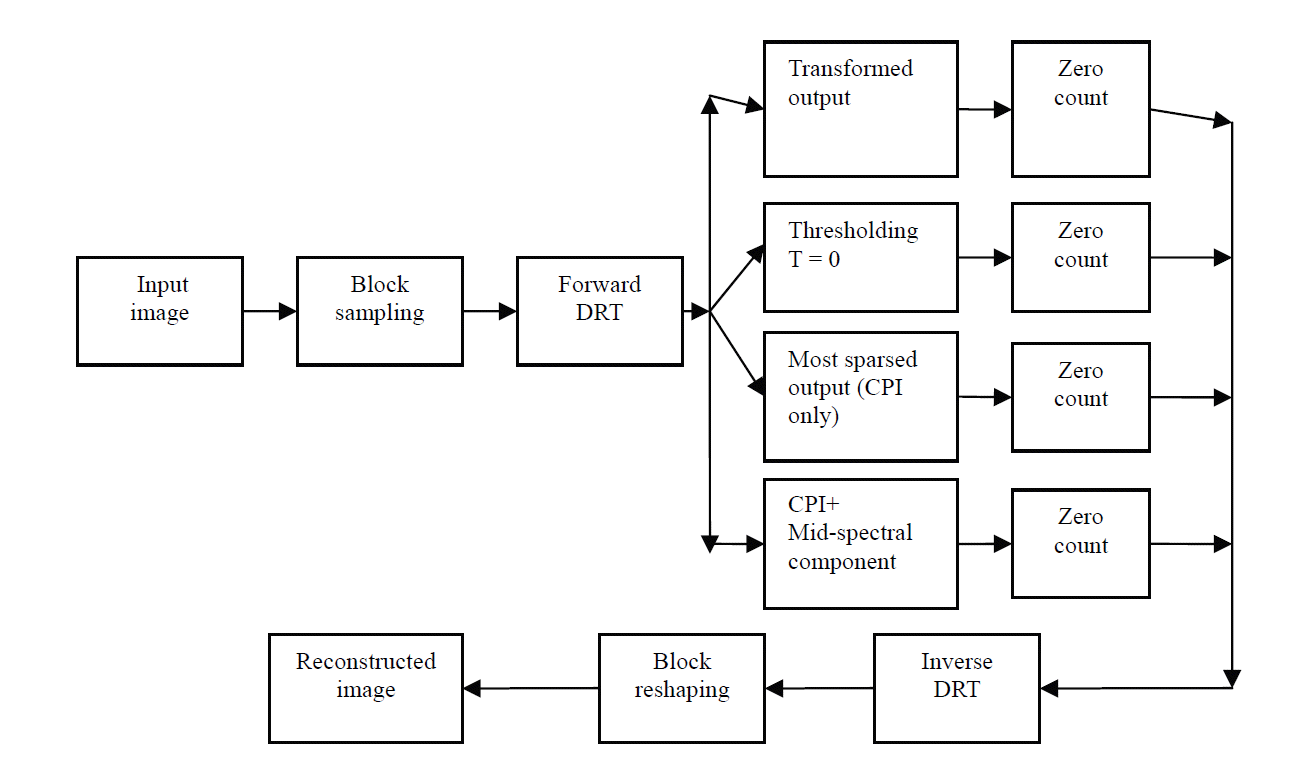
4.1 Block Diagram of the Proposed Algorithm
4.2 Proposed Algorithm
Input an image of dimension N×N.
Scan the image block wise.
-
Apply a forward transform (DRT/DCT/DFT/DWT) to obtain sparse output.
○ Case 1 (lossless): Calculate the degree of sparsity considering the transformed output as it is.
○ Case 2: threshold (threshold value T = 0) the transformed output and count the (N-K) sparse coefficients for calculating the degree of sparsity.
○ Case 3 (Most sparse case): Only retain the first spectral component value (the CPI in the case of DRT) and force the remaining components to zero for each block that is considered. Calculate the degree of sparsity.
○ Case 4: Retain the first spectral component and mid-spectral component and force the remaining components to zero for each block that is considered. Calculate the degree of sparsity.
On the receiver side, apply the inverse transform (IDRT/IDCT/IDFT/IDWT) to the spectrum data to recover the image data.
Reshape the blocks to obtain the final reconstructed image.
Calculate the PSNR and MSE.
The block diagram for this algorithm is shown in Fig. 3.
5. Simulation Results and Performance Analysis
For the purpose of simulation of DRT in different cases, different 512×512 input grayscale images (Lena, Cameraman, and Peppers) were used. Each of the input images was divided into 8×8-pixel blocks, the DRT was applied to it, and the degree of sparsity associated with the transformed signal output was calculated. Also, the scope of achieving the maximum possible sparsity was analyzed by applying a thresholding function, which, resulted in the loss of information in the signal.
For the simulation of DRT on the Lena image, out of the total 512×512 pixels, 9610 zero-valued or (N-K) sparse pixels were obtained. The degree of sparsity was obtained by using just the output-transformed signal of DRT, which was 3.7% (close to 4%). Similarly, for the Cameraman image, 10307 (N-K) sparse or zero-valued coefficients were obtained. The degree of sparsity obtained for the Cameraman image was 3.93% (close to 4%). For the Pepper image a similar trend was also observed. This was perfectly lossless and the original image was recovered with an infinite peak signal-to-noise ratio (PSNR) since no errors existed.
Further sparse representation of the transformed signal was obtained by applying the thresholding function. After thresholding (threshold T = 0) was considered for the Lena image, 134568 samples were approximated to be zero. The degree of sparsity that was obtained was 51.3%. Similarly, for the Cameraman image, the number of samples that could be approximated to zero was 180273 and the degree of sparsity achieved was 68.7%. For the Peppers image, the number of zero coefficients obtained was 131959 and a degree of sparsity close to 51% was achieved.
However, this can lead to the loss of information in the image and would then be classed as lossy. To have a visual perception of the sparsity and the amount of information lost, reconstruction using IDRT was done. Fig. 4 shows the reconstructed images after thresholding the transformed output of DRT to obtain a higher degree of sparsity.
It can be observed that there was a blocking effect in the image retrieved. The PSNR values of these images were found to range from 24–26 dB.
The sparsest representation possible using DRT was only when the CPI of each of the 8×8 blocks was considered (i.e., the information present in each of the 64 pixels in each block was represented by only one pixel and, thus, the total image can be represented by only 64×64 pixels). In this case, for all three of the images under consideration, the total number of zero coefficients possible was (512×512) – (64×64) (i.e., 258048) and the maximum achievable degree of sparsity was 98.44%. However, a considerable amount of information loss can be expected. To visualize the impact of the sparse representations, the image was reconstructed using the Inverse DRT process. The reconstructed images obtained in this case are shown in Fig. 5.
The PSNR for the lossy case mentioned above was found to be 20 and 24 dB, respectively. There is always a scope for improving the PSNR or compressing the signal by applying relevant algorithms. Similarly, the CPI value and the mid-spectrum value from the output of the DRT were considered. The CPI and mid-spectrum value of each of the 8×8 blocks were considered (i.e., the information present in each of 64 pixels in each block was represented by only two pixels and, thus, the total image can only be represented by 128×128 pixels). The PSNR obtained, in this case, ranged between 21–26 dB. Fig. 6 depicts the reconstructed images in this case. Table 1 depicts the degree of sparsity provided by DRT in lossless and lossy cases.

Reconstructed images when Cumulative Point Index and mid-spectrum values are retained in Discrete Rajan Transform output (block size 8×8).
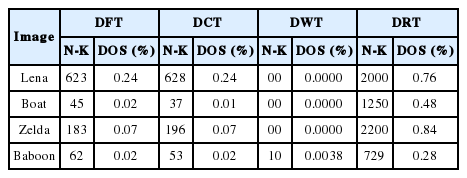
The performance of DRT in providing sparsity was also compared with what was provided by DFT, DCT, and DWT, by means of the degree of sparsity. This comparison is made in Table 2, which shows the degree of sparsity provided by different transforms for a block length of 28 (=256). For this analysis, four different types of benchmark images were used. For all of the images, the degree of sparsity provided by the DRT was better than that provided by other transforms. The reason for this is the nonlinear property of the DRT. In Fig. 2(b), it can be observed that the number of zero coefficients present in the DRT transformed output is higher than that of other transforms. And from Fig. 2(a), it can be observed that a greater number of coefficients in the DRT output have amplitudes less than zero. Hence, further sparsification can easily be achieved through using a thresholding operation (threshold value T = 0) with DRT to obtain improved compressibility.
6. Conclusions
In this paper, the widely used orthogonal transform basis functions DFT, DCT, and DWT were analyzed so as to obtain the sparse representation of images. DRT was introduced as a sparsifying transform and its purpose is to achieve both the lossless and lossy sparse representation of images. For a random input signal that is 256×1 in length, different block lengths (in powers of 2) were considered for all of the candidate transforms mentioned above. The total number of (N-K) sparse coefficients obtained was compared with different block lengths and it was found that up to the block length 24, DWT exhibited better sparse representation compared to DCT, DRT, and DFT. Beyond that, DRT produced about 24% of N-K sparse coefficients. For the maximum block length 27, DRT was able to produce an average of 98% sparsity. DFT and DCT, however, gave less than 1% N-K sparse coefficients. For different input images, the transformed signal output obtained from DRT achieved an an average of 23% achievable sparsity, thus exhibiting the possibility of achieving better sparse output when compared to the other three candidate transforms chosen for this research. In the perfectly lossless case that was discussed above, the original image can be recovered with an infinite PSNR since no errors exist. Also, further sparse representation through DRT can be obtained by using the thresholding function and by considering: only the CPI value and the CPI, along with the mid-spectrum values of each block in the transformed signal. However, both of the above-mentioned methods for obtaining better sparsity can be classed as lossy due to the loss of a significant amount of data.
7. Future Scope
For an image signal, DRT is able to provide a higher degree of sparsity by thresholding and by considering CPI values, CPI, and the mid-spectrum values of a DRT transformed output at different block lengths, but at the cost of loss in the information. DRT is capable of providing both lossless and lossy sparse representation. However, in this paper, only the application of DRT in relation to achievable sparse representation was focused on. Individual algorithms that help in improvising the PSNR and compressibility can always be employed.
There is always a scope to improve the degree of sparsity that is obtained in the cases that only take into account the CPI values or the CPI and mid-spectrum values. However, the compromise would be the loss of information in the signal.
Acknowledgement
We are sincerely grateful to Dr. E. G. Rajan, the Director of the Pentagram Research Centre in Hyderabad, India, and Ms. G. Prashanthi, MSc, from Staffordshire University in the UK, whose constant encouragement and guidance during the period of this work allowed us complete it with a clearer understanding of the subject.
References
Biography
Kethepalli Mallikarjuna http://orcid.org/0000-0001-9500-9187

He received B.E. and M.Tech. degrees in Department of Electronics and Communication Engineering (ECE) from Gulbarga University, Karnataka, India in 1991 and Jawaharlal Nehru Technological University, Hyderabad, Andhra Pradesh, India, in 2003, respectively. Since October 2008, he is with the Department of Electronics and Communication Engineering from Jawaharlal Nehru Technological University Kakinada, Kakinada as a part-time Ph.D. candidate. Also he is working as an Associate Professor in the School of ECE from Rajeev Gandhi Memorial College of Engineering and Technology, Nandyal, Andhra Pradesh, India. He has 20 years of teaching experience.
Kodati Satya Prasad

He received B.Tech. (ECE) degree from JNT University, Hyderabad, Andhra Pradesh, India in 1977, M.E. (Communication Systems) from the University of Madras, India in 1979, Ph.D. from IIT-Madras, India in 1989. He has more than 35 years of experience in teaching and 20 years in R&D. His current research interests include Signals & Systems, Communications, Digital Signal Processing, Radar, and Telemetry. At present, he is the Professor in Dept. of ECE, JNTUK Engineering College, Kakinada, Andhra Pradesh (state), India. He received Patent for his research work in 2015.
M. V. Subramanyam

He received B.E degree in Electronics and Communication Engineering from Gulbarga University, Karnataka, India, M.Tech. degree in Digital Systems and Computer Electronics from Jawaharlal Nehru Technological University, Hyderabad, Andhra Pradesh, India, in 1989 and 1998, respectively. Also, he received Ph.D. degree in Ad hoc Networks from Jawaharlal Nehru Technological University, Hyderabad, India in 2007. His current research interests include mobile communication and Computer networks. He has more than 24 years of teaching experience and six years of research experience. At present, he is the Principal of Santhi Ram Engineering College, Nandyal, Andhra Pradesh, India. He received Patent for his research work in 2015.