1. Introduction
Facial recognition was an interesting issue on the computer vision. The crucial problem of the facial recognition is high dimensional space [1]. Many methods have been developed to reduce high dimensional for both statistical-based [1–4] and geometrical-based [5,6]. The geometrically based method required high cost since the finding of features is randomly conducted and unstructured, therefore the computation time is extremely expensive and hard to be predicted. In addition, the different position of an object on the image has given the bigger distance than the same position, though they are in the same class. The geometrical-based method also produces the different features when the image features have the different expression for both the same and the different class so that the samples will be hard to be distinguished. In fact, the image samples utilized are random, and they have the different poses and expressions. The oldest method for feature extraction is the Principal Component Analysis (PCA) [2]. It has been developed by many researchers, because of simple, inexpensive cost, and fast computation [1]. PCA can change the correlated into uncorrelated variables. They are well known as the primary components.
The primary components provided are orthogonal vector basis because covariance matrix processed is symmetric matrix [7]. The results of the PCA process are less than the number of training data sets. However, the PCA cannot efficiently work when the number of original data sets is greater than the number of variables [1]. The PCA also produced the global structure as the dominant characteristics.
The PCA is improved by the Linear Discriminant Analysis (LDA). The LDA is generalized by the Fisher’s linear discriminant to obtain a linear combination. It is used to reduce the image dimensionality before the classification, or the recognition stage is conducted [8]. However, it has the weaknesses, i.e., the relationship of a variable to each other is always assumed a linear and global structure [9–12]. The appearance other methods such as two-dimensional Fisherface [1], Laplacianfaces [10], Gaussian Orthogonal Laplacianfaces [12,13] only produce the global structure and cannot represent the image features in detail, since they work on the input spaces to find the dominant features.
The Linear Preserving Projection (LPP) is the method that produces the local structure, but the LPP only able to map the linear function. In fact, the real data sets have non-linear distribution. The kernel is the right solution to map non-linear data distribution [14–17]. The global structure cannot depict the image in detail so that much information is lost when the feature extraction is carried out. In addition, distribution of the non-linear features cannot be separated by linear planes. In this research, the homogeneous and non-homogeneous are proposed to resolve the non-linear image samples by using the linear planes. The data sets are mapped by using homogeneous and non-homogeneous polynomial kernel function as the proposed method. The mapping results were further processed to obtain the eigen and followed by the training set projection in the feature space. The weight features are also obtained as the multiplication results between the training sets and eigenvector in the feature spaces. Homogeneous and non-homogeneous polynomial-based eigenspaces cannot work in the image space, but they can only optimally perform in the feature space so that the image samples provided are in the feature space, and the missing information of features can be significantly minimized.
To make clear the paper, the remaining of the paper was designed as follows. The Section 2 will be in detail clarified the proposed method. Section 3 construes the experimental results of the proposed method in detail. Section 4 will make an analysis of the experimental results. The resume of this research will be written in Section 5.
2. The Proposed Method
Homogeneous and non-homogeneous polynomial are used to acquire the feature extraction results in the feature space. The feature space can be obtained by mapping of the input space. The input space is a representation of the training sets, whereas the training sets are a collection of the vector space. The vector space is denoted by using the row vector of the facial image as formulated in equation,
The row vector of the facial image as written in (1) can be formulated by using one-dimensional matrix as follows,
If the dimensional matrix is represented by using n, where n = h × w (h states the height image and w states the image width), then the (2) can be re-formulated as follows,
The (1)–(3) show that the value of f(x, y) is the member of ℝ, (f(x, y) ∈ ℝ1,n). In this case, n represents the facial image dimensions. If the training sets are signified by using m, then the dimensionality of the training sets ∈ ℝm,n, where m = c × t, c states number of classes and every class has t poses, the input space of the training sets ℝm,n must be mapped into feature space.
2.1 Homogeneous and Non-homogeneous Polynomial
In this research, homogeneous and non-homogeneous polynomial are offered to map from input to the feature space using the kernel trick. For both homogeneous and non-homogeneous polynomial produce feature space in the ℝm,n. In this case, the homogeneous polynomial can be designated by using KH(Φ(x), Φ(xT)) as follows,
(4)
The left and the right bracket indicate ΦH(x) and ΦH(xT). The (4) is implemented to map from the input to feature space, where a further process is not using the input space but feature space. The process has reduced the quantity of the object dimensionalities. Therefore the computation can be minimized for the further process. Besides the homogeneous polynomial, non-homogeneous polynomial is also offered to convert from input space into feature space, which is KN(Φ(x), Φ(xT)). Non-homogeneous can be stated as heterogeneous of the features or the mixture of the different object characteristic. It has more parameters than the homogeneous polynomial since the non-homogeneous represents assortments of the dominant features. It can be formularized as follows,
2.2 New Feature Space in Homogeneous and Non-homogeneous Polynomial
To simplify the writing of the equation, for both new feature space of the homogeneous and non-homogeneous, the parameter of K(Φ(x), Φ(xT)) is performed to represent for them. It means that the variable of K(Φ(x), Φ(xT)) states KH(Φ(x), Φ(xT)) for homogeneous or KN(Φ(x), Φ(xT)) for non-homogeneous feature spaces.
The novelties of the proposed approach are the modeling of the new feature spaces and symmetrical matrix of them. They are Mj,k(Φ(x), Φ(xT)) and Nj,k(Φ(x), Φ(xT)), where Mj,k(Φ(x), Φ(xT)) states the new feature spaces, while Nj,k(Φ(x), Φ(xT)) represents the symmetrical matrix of the new feature spaces. Several stages have been created to obtain the new feature spaces and the symmetrical matrix of them, i.e., by computing the S1(Φ(x), Φ(xT)), S2(Φ(x), Φ(xT), S3(Φ(x), Φ(xT)), S4(Φ(x), Φ(xT)), and S5(Φ(x), Φ(xT)).
The calculation of the new feature space can be obtained by the values of the S1(Φ(x), Φ(xT)), S2(Φ(x), Φ(xT)), S3(Φ(x), Φ(xT)), S4(Φ(x), Φ(xT)), and S5(Φ(x), Φ(xT)). They can be stated by the equation,
The (6) is utilized to acquire the matrix with the same value on each column, while the (7) is used to gain the same value on the same row. The results will be implemented to calculate the new feature space of Nj,k(Φ(x), Φ(xT)),
The (9) is aimed to acquire the values of the Kj,k(Φ(x), Φ(xT)) matrix. To maximize the information gained, the results of (8) and (9) are compared to find the maximum value as follows,
The variables of j and k state an indexing of the row and column, where j, k ∈ 1, 2, 3, ⋯, m. Meanwhile the parameter of Γj,k indicates the matrix, where all matrix elements have “1” values, it has the same size with Kj,k(Φ(x), Φ(xT)) matrix. The dimensionality of Mj,k(Φ(x), Φ(xT)) can be represented by m for both row and column, therefore the matrix of Γj,k has also size m for both row and column as follows,
To obtain the symmetrical matrix of the new feature space, the result of (12) is summed with its transpose matrix as follows,
The calculation result of (13) is applied to acquire the eigenspace in the new features space. It has also m dimensional for row and column. The proposed method has produced the orthogonal matrix as shown in (13). The matrix can preserve the important information of the object before it is further processed in the feature spaces.
2.3 Eigenspace in Feature Space
The proposed method has significantly reduced the dimensionality of the image input as shown in (6), (7), (8), (9), (10), (12), and (13). The result of (13) is utilized as the sample input on the further stage. In this stage, the eigenspace was proposed to obtain the weight and projection matrix in feature space. The new feature space of the result of (13) is further processed to obtain the eigenspace in feature space, Firstly, mean of the new feature space is calculated as seen in equation,
The result of (14) is applied to compute the zero mean in the new feature space as written in the equation,
In (15), the calculation result delivers the matrix with m size for column and row. It is caused by the index of j, ∀j ∈ 1, 2, 3, ⋯, m. Similarly, it is also occur for the index of k, ∀k ∈ 1, 2, 3, ⋯, m. The covariance matrix in the new feature space can be calculated by using the matrix multiplication result between (15) and its transpose as written in equation,
The generalized eigenvalue problem is performed to acquire the solutions of the (16). The results are the eigenvalues λk, j and their eigenvectors Λj,k(Φ(x), Φ(xT)) for further processing. The eigenvalues are sorted in descending order, λ1,1 > λ2,2 > λ3,3 > ⋯ > λm,m and followed by the column elements of the eigenvectors as follows,
(17)
The advantages of the proposed method are the capability to separate the image with the different poses and expression. Therefore the images with the different classes are easier to be classified. Meanwhile, the disadvantage of the proposed approach is incapability of the homogeneous and non-homogeneous to recognize the face image with the illumination effect.
2.4 The Weight and Projection of the New Feature Space in Homogeneous and Non-homogeneous Polynomial
The eigenvectors associated with the largest to smallest eigenvalues are utilized to calculate the projection and weight in the new feature space. The projection of the new feature space is the multiplication results of the zero mean matrixes and the eigenvectors as follows,
To speed up the process, the eigenvectors of the new feature space can be normalized as shown in (19), (20), and (21). ∀k, k ∈ 1, 2, 3, …, m. The (19) is computed based on the column summation as represented in equations,
The result of (20) is further operated by using “dot product operation” for each ∀j, j ∈ 1, 2, 3, …, m. The normalized projection matrix can be produced by “dot product operation” of the (21),
The operator of " ∘ " states “dot product” between the values of the Pj,k(Φ(x), Φ(xT)) and P̌ j,k(Φ(x), Φ(xT)). The result of (21) asserts the normalized projection matrix of the training sets. The results are applied to calculate the weight of the training sets Wj,j(Φ(x), Φ(xT)) as follows,
The result of the (22) represents the feature of the training sets. For each column of the weight matrix depicts the characteristics of the training sets. As it is knows that the index of j, and k have the same index number, i.e. ∀k, k ∈ 1, 2, 3, …, m. and ∀j, j ∈ 1, 2, 3, …, m. Therefore, the value of Wj,j(Φ(x), Φ(xT)) is also can be written by using Wk,j(Φ(x), Φ(xT)).
2.5 The Similarity Measurements
In this research, the distance of the image features will be applied to measure the weight of the training and the testing sets. The feature extraction result of the testing sets will be calculated and compared to the training sets. In this case, the classifier used for the measurement is the Euclidean distance method,
In this case, the value of Ŵj,1(Φ(x), Φ(xT)) states the weight features of the testing sets, whereas Wk,j(Φ(x), Φ(xT)) depicts the features of the training sets. The most minimal value of Dk is considered as the similar image on the kth index.
2.6 The Algorithm of the Proposed Method
In this research, the proposed method has been written by using the algorithm. The outputs of the algorithm are the projection matrix P⃛j,k(Φ(x), Φ(xT)) and the weight matrix Wj,k(Φ(x), Φ(xT)). The projection matrix is used to obtain the weight of the testing sets Ŵj,1(Φ(x), Φ(xT)). The weight features of the testing sets were compared to the weight features of the training sets. The algorithm of the proposed method can be composed as follows
Algorithm 1
Algorithm of the proposed approach
The proposed algorithm is the improvement results of the previous algorithm, i.e., the Eigenface, Laplacianfaces, Fisherface, and O-Laplacianfaces. The proposed algorithm can separate the non-linear data sample by the linear plane. The proposed algorithm can recognize the facial image with the different poses, and expressions, while the image with illumination should be normilized first before processing.
Algorithm 1 represents the novelty of the proposed method, where the process is started by computing of the homogeneous and non-homogeneous polynomial (see line 1 and 2), whereas the 2nd line until 6th are utilized to compute the value of S1j,k(Φ(x), Φ(xT)), S2j,k(Φ(x), Φ(xT)), S3j,k(Φ(x), Φ(xT)), S4j,k(Φ(x), Φ(xT)), S5j,k(Φ(x), Φ(xT)), Mj,k(Φ(x), Φ(xT)), and Nj,k(Φ(x), Φ(xT)). The 7th until 11th compute the mean of the feature space μ1,k(Φ(x), Φ(xT)), moreover the zero mean of the new feature space can be described on the 12th until 14th line, while the 15th until 19th line explain the covariance matrix on the new feature space. The eigenvalues and eigenvectors calculation can be seen in the 20th line. The results of the eigenvalues are sorted and followed by the eigenvectors of the new feature spaces. Their results are implemented to obtain the projection matrix as explained on the 22nd until 26th lines, while to obtain the weight matrix can be described on the 27th until 31st lines. The results of the weight matrix will be used to calculate the similarity between the training and the testing sets.
This algorithm does not only reduce the image dimenionality, but also compute the projection matrix as shown on the 22nd until 26th lines, and compute the weight of the training sets as shown on the 27th until 31st lines. The projection matrix is applied to get the weight of the testing set, whereas the weight of the testing set will be moreover compared to the weight of the training sets using the Euclidean distance method as shown in (23).
3. Experimental Results and Analysis
The proposed method was evaluated by using three image databases, i.e., the Olivetti Research Laboratory is well known as ORL, the YALE, and the University of Bern (UoB or UB). The proposed method applies four kind models, i.e., for each image database uses two, three, four, and five training sets. The remaining of the samples was used as the testing sets. For each database has the different number of classes. The features measured are influenced by the number of classes (c). Minimum features implemented are c+1, whereas the maximum features applied are twice of c. Therefore, for each class has the different number of features as shown in Table 1. In this research, MATLAB R2008a is applied to perform the proposed approach.
3.1 Experimental Results on the YALE Database
The YALE has 165 facial images with the different model, i.e., an expression, an illumination, and an accessory. Fifteen persons were captured with the different models. An expression model has six variants, i.e., happy, normal, sad, surprised, wink, and sleepy. The illumination model has three variants, i.e., the centre, the left, and the right illumination, whereas an accessory model uses glasses and no glasses [18]. The image samples of the YALE can be seen in Fig. 1.
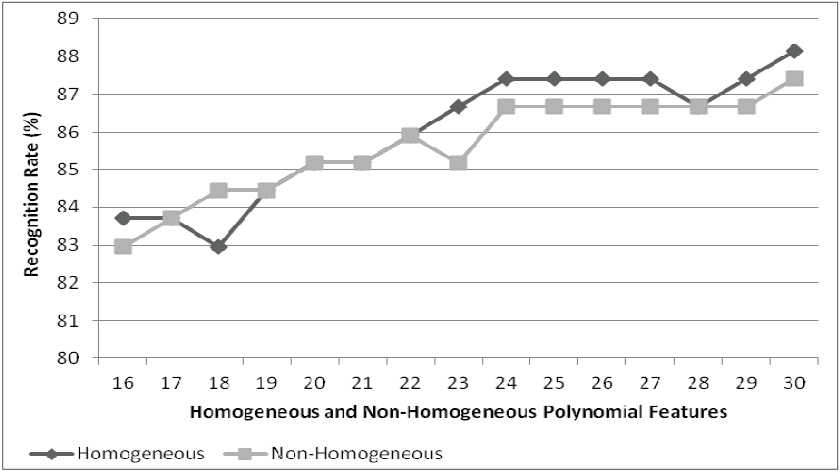
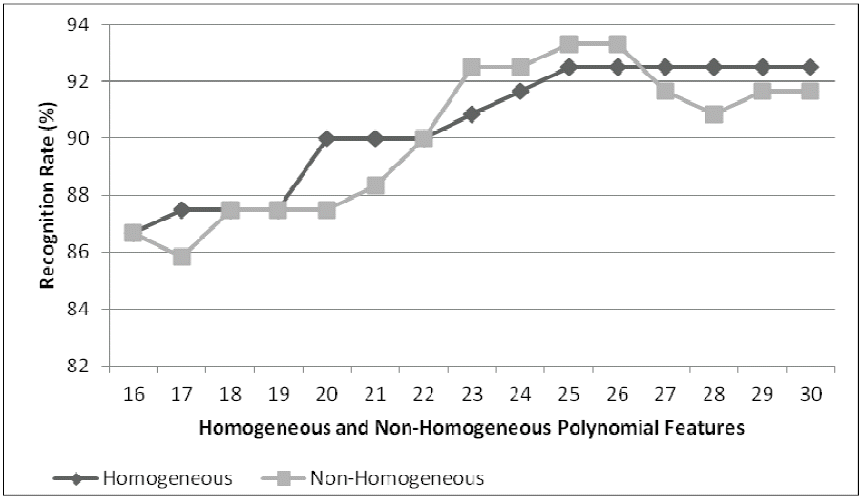
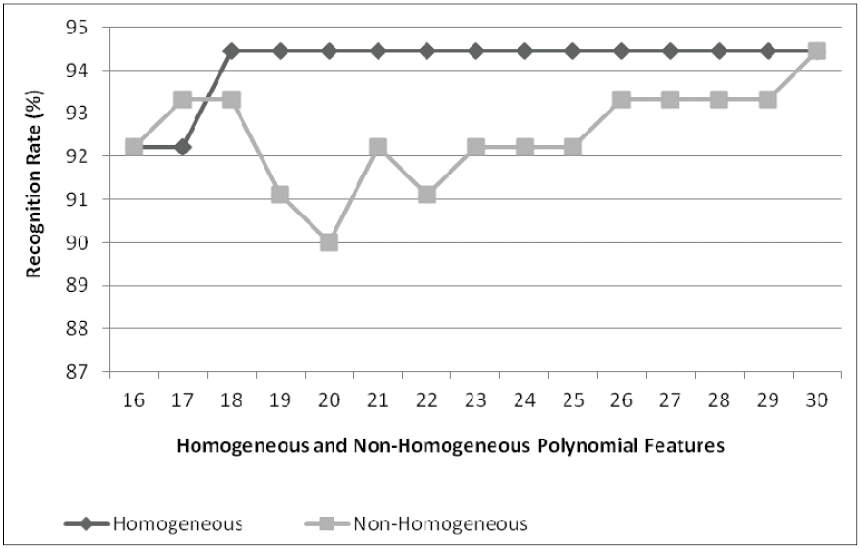
The experiment result was provided by using several scenarios as seen in Table 1, i.e., two, three, four, and five images as training sets. For each scenario was evaluated 15 times, which are using 16 until 30 features. The (4) and (5) were used to map the input to feature space. The experimental results of the proposed method, for both the homogeneous and the non-homogeneous polynomial can be seen in Figs. 2–5.
Experimental results as shown in Figs. 2–5 for both the homogeneous and the non-homogeneous polynomial produce recognition rate proportional to the number of features used though there is deviation on the particularized points. Fig. 2 has shown that the more training sets used, the higher recognition rate produced. The homogeneous polynomial returns the higher recognition rate than the non-homogeneous polynomial. The different results were shown in Figs. 3 and 4. It displayed that the non-homogeneous polynomial had produced higher recognition than the homogeneous polynomial. Fig. 3 has performed that the non-homogeneous polynomial produced the higher recognition rate than the homogeneous polynomial when using 23 until 26 features, whereas for other features, the non-homogeneous polynomial has returned the lower recognition rate than the homogeneous polynomial. In Fig. 5, the homogeneous polynomial obtains the highest recognition rate from 18 until 30 features, which is 94.4%. The different results have occurred on the non-homogeneous polynomial. It has produced the lower recognition rate than the homogeneous polynomial from 18 until 29 features. On the last features, the homogeneous and the non-homogeneous polynomial has delivered the same recognition rate, which is 94.4%.
The proposed method has produced maximum recognition rate on the YALE database, which is 94.4% for both the homogeneous and the non-homogeneous polynomial when using five training sets. The highest recognition rate for each training sets can be seen in Table 2. For both the homogeneous and non-homogeneous polynomial has proved to separate the face image with the different pose and expressions, while the face image with different illumination still remain the problem when the similarity measurement was performed. The effect of an illumination has delivered incorrect classification on the image testing sets. Therefore, it is important to improve the image input, so that the image input does not have the effect of an illumination. In this case, the illumination normalization process is applied to remove the image illumination.
3.2 Experimental Results on the ORL Database
Many researchers have utilized the Olivetti Research Laboratory (ORL) database to evaluate their proposed methods. The proposed algorithm was also evaluated using the same database, i.e., ORL. The ORL database has forty persons with the different expression, accessory, and pose. The expressions of the ORL facial image are open eyes, closed eyes, smiling, and neutral. The poses of the ORL facial image are right, left, up and down [19]. The accessories of the ORL facial image are using glasses and no glasses. The sample of the ORL database can be shown in Fig. 6. The dimensionality of the ORL face image is 112 for the height and 92 for the width, therefore the ORL dimensionality is 10.304 (112×92).
The experimental scenarios have also followed an instruction as shown in Table 1, i.e., four scenarios. The first scenario, the proposed method has been evaluated using two images as training sets. The second until the last scenarios using three, until five images as training sets. The experimental results have been explained in Figs. 7–10. They are graph results using two, three, four, and five images as training sets respectively. The face image features applied are 41 until 80. The proposed method has significantly reduced the image dimensionality, i.e., more than 10.200 (10.304–80=10.224) features. The dimensionality reduction has significantly reduced the computation time when the classification is carried out.
In Fig. 7, the non-homogeneous polynomial has produced higher recognition rate than the homogeneous polynomial from 60 until 80 features. In this case, the maximum recognition rate for the non-homogeneous polynomial is 77.18%, whereas for the homogeneous polynomial is 76.25%. It can be concluded, the highest recognition rate for two training sets is the non-homogeneous polynomial.
The similar results have also occurred in Fig. 8, where the non-homogeneous polynomial has produced the higher recognition rate than the homogeneous polynomial. The maximum recognition rate for three training sets is 92.86%. The largest acceptance for each the training sets can be found in Table 3.
The different results have been displayed in Figs. 9 and 10. In Figs. 9 and 10, the homogeneous polynomial is superior to the non-homogeneous polynomial. Moreover, for four training sets, the homogeneous polynomial has surpassed the non-homogeneous. For five training sets, the homogeneous polynomial has produced higher recognition rate than the non-homogeneous polynomial almost for all features.
The ORL face image database has normal distribution on the illumination, where the image has been captured on center of the lighting. Therefore, the error produced of the ORL is lower than the YALE face image database. The image with the illumination effect cannot be correctly classified when the similarity measurements were performed. It is caused by the face image with the illumination more similar to another class than the same class, so the image with illumination is not correctly classified.
The different results have been displayed in Figs. 9 and 10. In Figs. 9 and 10, the homogeneous polynomial is superior to the non-homogeneous polynomial. Moreover, for four training sets, the homogeneous polynomial has surpassed the non-homogeneous. For five training sets, the homogeneous polynomial has produced higher recognition rate than the non-homogeneous polynomial almost for all features.
The ORL face image database has normal distribution on the illumination, where the image has been captured on center of the lighting. Therefore, the error produced of the ORL is lower than the YALE face image database. The image with the illumination effect cannot be correctly classified when the similarity measurements were performed. It is caused by the face image with the illumination more similar to another class than the same class, so the image with illumination is not correctly classified.
3.3 Experimental Results on the University of Bern (UoB) Database
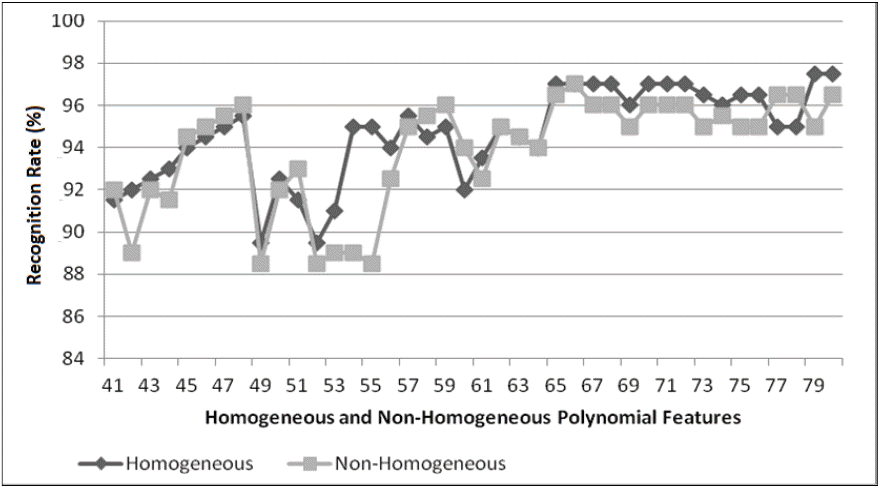
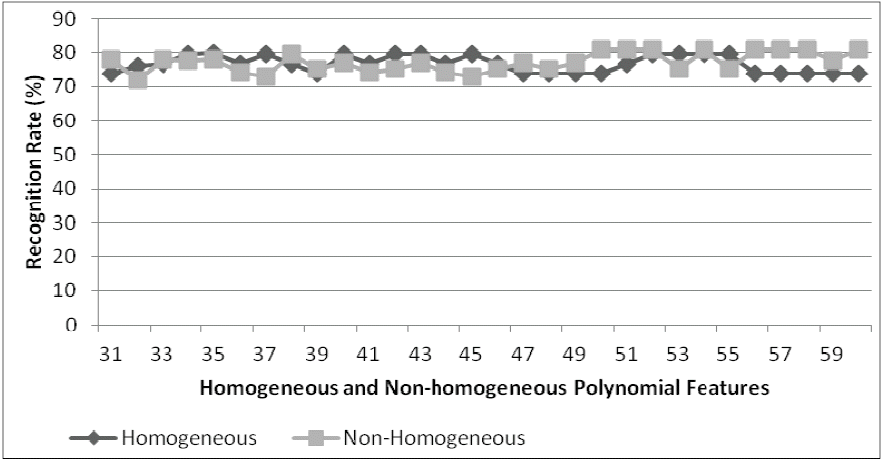
The University of Bern has 300 images. The images were captured from thirty persons. For each person has ten different poses. The original image has 512 pixels in height and 342 pixels in width [20]. The original images were resized to 140 pixels in height and 120 pixels in width to evaluate the proposed method. Image samples of the UoB are shown in Fig. 10. The experiment was also performed using instruction as shown in Table 1. In this research, experimental was conducted using four scenarios. For each scenario was evaluated thirty times, i.e., using 31 until 60 features. The experimental conducted is one hundred and 20 times for both homogeneous and non-homogeneous polynomial. The results can be seen in Figs. 12–15.
Fig. 12 demonstrates the experimental results on the UoB database of the proposed method using two training sets, and the rest of the samples are applied as the testing sets. In general, the experimental results show that non-homogeneous polynomial outperformed to homogeneous polynomial, though on the certain features, homogeneous polynomial produced higher recognition rate than non-homogeneous polynomial. Although only uses two images as training, but the proposed method is able to recognize the image of almost 80%, i.e., non-homogeneous polynomial obtained 78.33% recognition rate, whereas for homogeneous polynomial is 75.83%. In this case, the proposed method proved that mapping from input space into feature space can reduce error rate in recognition. Besides that, the homogeneous and non-homogeneous polynomial are also able to agglomerate the same classes, and to separate the different classes. The results have indicated that the proposed method is able to separate the image, even though the training sets used as training sets less than 25%. It also proved that the proposed method can optimally perform on the small samples size, where number of the training sets is less than the dimensionality used. It means that the selection function is an important role in mapping from the input space into feature space.
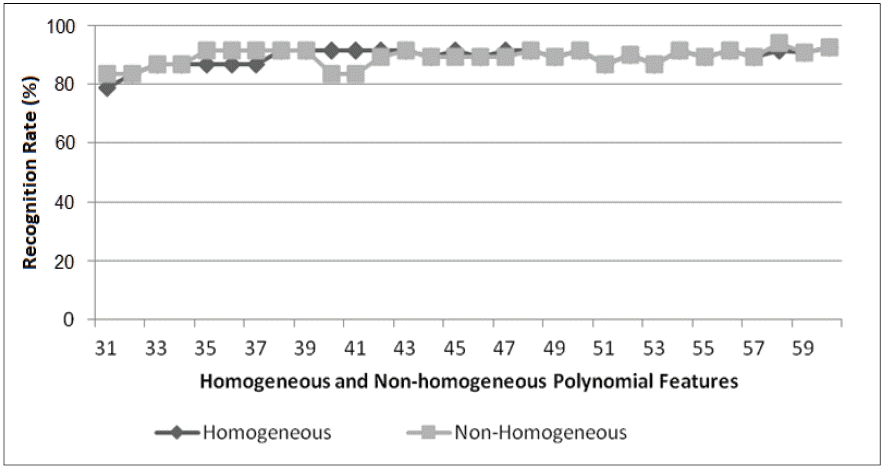
The similar results were also demonstrated in Fig. 13, the experimental results using three training sets on the UoB database. Experimental results of the proposed method show that the non-homogeneous polynomial has produced 80.95% as maximum recognition rate, whereas the homogeneous polynomial has produced 76.67% as maximum recognition rate. It means that the non-homogeneous polynomial outperformed to homogeneous polynomial.
The similar result occurs in Fig. 14. In general, the non-homogeneous polynomial has produced the higher recognition rate than the homogeneous polynomial. The homogeneous polynomial only returned 82.78% as maximum recognition rate, whereas non-homogeneous polynomial has produced 84.44% as maximum recognition rate. It shows that the increasing of the homogeneous polynomial is still under the increasing of the non-homogeneous polynomial.
The last result on the UoB database has delivered 92.67% recognition for the homogeneous polynomial, whereas 94% recognition rate was produced by the non-homogeneous polynomial as shown in Fig. 15 and Table 4. On the last results show that the non-homogeneous polynomial delivered better recognition rate than the homogeneous polynomial.
The results of the UoB database showed that the largest recognition rate of the proposed method was delivered by using five training sets, which is the non-homogeneous polynomial (94%), meanwhile the lowest recognition rate is delivered by two training sets for the homogeneous polynomial (75.83%). The homogeneous polynomial and non-homogeneous polynomial have delivered the recognition rate proportional to the training sets used. The increasing of the training sets has made effect to the increment of the recognition rate. In general, the non-homogeneous polynomial has obtained the higher recognition rate than the homogeneous polynomial.
The proposed method has maximally recognized 94% of the image testing, 6% wrong classification is caused by the object similarity of the image from the different class, so that the distance between a class and the others is smaller than the distance on the same class. Therefore, the measurement results of the object similarity show that the smallest difference of the distance inclined close to the image of the different class.
4. Performance Evaluation of the Proposed Method with Other Methods
The proposed methods are homogeneous and non-homogeneous polynomial. They have mapped from the input to feature space. The mapping results have been extracted the features. Further processing is similarity measurements of the features. The experimental results are conducted several times on the different databases. The experimental results are evaluated and compared to other methods. They are Eigenface, Fisherface, Laplacianfaces, and Orthogonal Laplacianfaces or well known as O- Laplacianfaces.
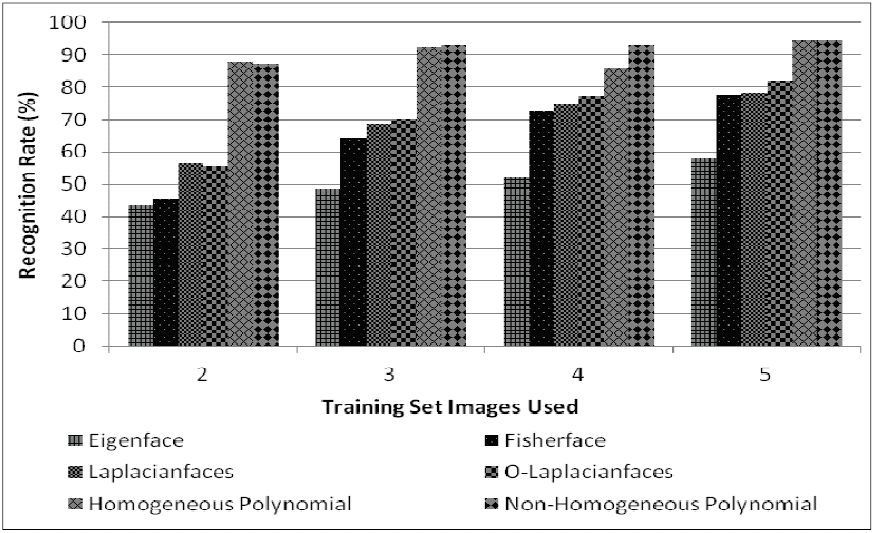
On the YALE database, the proposed methods (homogeneous polynomial and non-homogeneous polynomial) produced higher the recognition rate than other methods, such as Eigenface, Fisherface, Laplacianfaces, and O-Laplacianfaces. Even, the difference of recognition rate between the proposed methods and other methods are significant as seen in Fig. 16.
The similar case is also produced when the ORL face image database is used as the training sets. The experimental results using two, three, and five training sets show that the proposed method (homogeneous polynomial and non-homogeneous polynomial) outperformed to other methods, i.e., the Eigenface, Fisherface, Laplacianfaces, and O-Laplacianfaces. However, the O-Laplacianfaces has produced the higher recognition rate than other methods, which are Eigenface, Fisherface, and Laplacianfaces included the proposed method when using two training sets as shown in Fig. 17.
The last performance evaluation is the comparison of the experimental results on the UoB database as described in Fig. 18. In general, the proposed methods are better than other methods, such as the Eigenface, Fisherface, Laplacianfaces, and O-Laplacianfaces. It shows that the homogeneous and non-homogeneous polynomial based Eigenfaces are suitable to extract the face images, though they are influenced by illumination effects, pose variants, and accessories.
The proposed algorithm can well perform on the different pose and expressions though on the different classes. It can be proved based experimental results on the YALE and ORL, but the image with the different illumination cannot be well dissociated. The proposed approach also has limitation on the image testing that has the object similarity to the different class. If two objects of a different class but has some similarities object will tend to have different small distance, so that the measurement results also have a tendency wrong. The proposed method has not been able completely to distinguish two different classes, but has some similarities the object, so that the necessary improve method to maximize the distance difference from the different classes has some similarities though the object.
5. Conclusions
In this paper, the proposed method has shown that homogeneous polynomial and non-homogeneous polynomial could be used to map from the input into feature spaces and to extract the object characteristics in feature spaces. It can be proved from the experimental results on three databases. The experimental results showed that the highest recognition rate obtained are 94.44%, 97.5%, 94% on the YALE, ORL, and UoB databases, respectively. The experimental results have also demonstrated that the recognition rate is induced by the training sets used. It proved that the recognition rate result is proportional to the number of training sets used. The proposed method, for both homogeneous polynomial and non-homogeneous polynomial also have shown that the experimental results superior to Eigenface, Fisherface, Laplacianfaces, and O-Laplacianfaces on the YALE and the UoB databases for two, three, four and five training sets. On the ORL database, O-Laplacianfaces has obtained the higher recognition rate than the proposed method for both homogeneous polynomial and non-homogeneous polynomial. They are obtained through two images of the training sets, but for three, four and five training sets, the proposed method has produced the higher recognition rate than Eigenface, Fisherface, and Laplacianfaces, included O-Laplacianfaces.
The proposed approach has proved that the image with the different poses, and expressions can be correctly recognized, meanwhile the image with illumination is necessary to be normalized before processing, because the illumination has effected on the image, so that it similar to the other classes. Experimental results displayed that several misclassifications have occurred through recognition rate graph. Many errors in the classification due to illumination effects on the image, therefore the illumination effect on the image should be reduced to normalize the gray of the image. For further research, Misclassification can be reduced by image enhancement to normalize the illumination effect on the image.