Mohd-Hilmi, Al-Laila, and Malim: Accelerating Group Fusion for Ligand-Based Virtual Screening on Multi-core and Many-core Platforms
Abstract
The performance issues of screening large database compounds and multiple query compounds in virtual screening highlight a common concern in Chemoinformatics applications. This study investigates these problems by choosing group fusion as a pilot model and presents efficient parallel solutions in parallel platforms, specifically, the multi-core architecture of CPU and many-core architecture of graphical processing unit (GPU). A study of sequential group fusion and a proposed design of parallel CUDA group fusion are presented in this paper. The design involves solving two important stages of group fusion, namely, similarity search and fusion (MAX rule), while addressing embarrassingly parallel and parallel reduction models. The sequential, optimized sequential and parallel OpenMP of group fusion were implemented and evaluated. The outcome of the analysis from these three different design approaches influenced the design of parallel CUDA version in order to optimize and achieve high computation intensity. The proposed parallel CUDA performed better than sequential and parallel OpenMP in terms of both execution time and speedup. The parallel CUDA was 5–10× faster than sequential and parallel OpenMP as both similarity search and fusion MAX stages had been CUDA-optimized.
Key words: Chemoinformatics, Graphical Processing Unit, Group Fusion, Open Multiprocessing, Virtual Screening
1. Introduction
Chemoinformatics is concerned with the application of computational methods to solve chemical problems, with particular emphasis on the manipulation of chemical structural information [ 1]. The topics covered, such as chemical database design, information searching and retrieval, Chemoinformatics applications of high-throughput screening (HTS), and molecular modeling, have rapidly become an essential component of the main body of Chemoinformatics. Virtual screening (VS) is one of the methods used to find similarity between chemical compounds [ 2]. Ligand-based virtual screening involves methods such as similarity searching (SS) which involves searching for compounds of interest by evaluating the likeliness (or similarity) of chemical database compounds to a given input (reference compound) using similarity coefficients [ 3]. It seeks similar chemical compounds and returns results ordered by which compounds tend to have the most similarity. Given a query compound, similarity searching finds chemical compounds in the database that have a high percentage of unique features that are common to both. At the end of the search, a list of chemical compounds is obtained, ranked by most similar by sorting the list in descending order based on their similarity scores. Finally, the result of the similarity search will perform an optimizing precision/recall over sample of that result.
Data fusion is a technique that combines the results of similarity searches [ 4]. A similarity search campaign with multiple queries of compounds using a database of compounds produces a series of results of individual searches that contain ranks [ 5]. These results are then combined (or fused) into a single ranking list. Combining the results was found to perform on average slightly better than individual searches since fusion provides more divergence in the ranks of search lists. Group fusion is one of the branches of data fusion techniques that are used in Chemoinformatics. It combines the results of similarity searches based on multiple query compounds on the same representation with a single similarity coefficient. One of the goals of using group fusion is to measure the degree of structural diversity of molecules. In a previous work by Hert et al. [ 6], they observed that the combination of fingerprints with group fusion of scores was more effective when applied in virtual screening. Whittle et al. [ 7] concluded that improvements were observed when using group fusion instead of conventional similarity searches. Good performance was recorded using the Tanimoto coefficient, while poor performance was obtained with Forbes, Russell-Rao, Simpson and Yule coefficients. The implementation of GPUs in Chemoinformatics has recently increased. Vogt and Bajorath [ 8] described in their work that a number of studies have focused on using GPUs to address computational efficiency of different virtual screening methods. The focal point of implementing GPUs has also broadened to include Chemoinformatics procedures such as similarity searching and clustering. Two additional factors contribute to motivate the development of efficient implementations: the popularity of high-dimensional fingerprints as descriptors (such as extended connectivity fingerprints or MolPrint2D), affordable GPUs that are cheaper in the market and the availability of application programming interfaces such as CUDA (compute unified device architecture) that spur the implementation of parallelization of codes. A recent work by Sanchez-Linares et al. [ 9] used grid kernels for virtual screening in GPU with 200 ligands increased the speed by 20× and 30× for both Fermi and Tesla architecture versus sequential grid kernel. Maggioni et al. [ 10] provided a very deep analysis regarding the advantages of using GPU by assessing five different similarity coefficients with binary fingerprints and floating point descriptors as compound representations. The results from their work showed a significant speedup of both low-end GPU machines and high-end GPU machines, thus solidifying the usefulness of GPUs in Chemoinformatics. Most of the work on multi-core and GPU is related to conventional similarity searching. In this paper, we discuss the implementation of group fusion on both platforms. This section provided the latest updates on similarity searching implementations on multi- and many-core platforms. The next section presents the background of similarity searching and group fusion. This is followed by parallel design methodology and implementation before proceeding to discussions on results and conclusions.
2. Background
This section presents a discussion of chemical databases, chemical compound fingerprints, similarity coefficients, similarity searching and group fusion, as well as the emergence of multi-core and GPU implementation of similarity searching.
2.1 Chemical Databases
Chemical databases are also known as drug databases. These databases store information related to chemical compound bioactivity whether they were synthesized and proven to be active or inactive. There are a number of drug databases that are widely available such as the following:
World Drug Index (WDI) database is a collection of 80,000 marketed and developmental drugs worldwide sourced from 1,200 scientific journals and conference proceedings [11]. DrugBank is a public database consisting of compounds extracted from protein sequence databases, medicinal chemistry textbooks and chemical reference handbooks [12]. The 2011 Release contains 6,827 drug entries, as specified on their website. MDL Drug Data Report (MDDR) is a commercial database containing 185,844 (2008.1 Release) compounds that are newly launched or under development, extracted from patent literature, journals, meetings and congresses [13]. National Cancer Institute databases is a combination of four smaller databases that includes the general NCI database, the Plated Compounds database, the AIDS database and the cancer database, which sum up the total compounds residing in it to 213,000 [14].
2.2 Chemical Compound Fingerprints
A chemical fingerprint is a unique pattern that indicates the presence of a particular chemical fragment in a chemical compound. It is based on a bitmap representation and binned into 512-bit or 1024-bit [ 15, 16]. In similarity search, the use of fingerprints can be very useful for finding related molecules (example shown in Fig. 1). Chemical compounds are stored in a chemical database as a string of SMILES (i.e., simplified molecular input line entry system) that are then converted to a chemical fingerprint. Creating a fingerprint requires the system to hash all the molecular features. Many distinct encodings of fingerprints can be generated depending on the software used. The work of Hert et al. [ 6] presented detailed literature on most of them. Software is made available by licensing from various vendors, one of which is Scitegic. Scitegic’s ECFP (extended connectivity fingerprints presence) fingerprint [ 17] is a type of circular fingerprint that encodes the presence and absence of fragments in a compound in binary where “1” denotes presence and “0” denotes absence [ 18]. They also developed extended connectivity fingerprints count (ECFC) fingerprint that encodes the number of times fragments appear in the compound that is also known as floating point descriptors. Fig. 1 shows an example of ECFP and ECFC fingerprints. Note that “4” illustrated at the end of both fingerprint labels denotes the bond radius since a circular fingerprint is developed to characterize fragments that are centered on an atom along with the bonds encircling it [ 18], in this case a 4-bond radius.
2.3 Similarity Coefficients
Given fingerprints of two chemical compounds, their similarity can be computed using a similarity coefficient. Similarity coefficients are actually formulae used to quantify the degree of resemblance between compounds. They can be grouped into two main classes: distance and association coefficients as described by Salim et al. [ 19]. Distance coefficients measure the dissimilarity between compounds [ 20] by calculating the distance between them in a descriptor space. Compounds are identical if their positions coincide, i.e., the distance between them is 0. Thus, as the distance increases, the probability of compounds being similar decreases. In contrast to distance coefficients, association coefficients measure the agreement (similarity) between two compounds [ 20] where the value also ranges from 0 to 1, but 0 indicates no similar features in common, while 1 indicates an identical match [ 19]. Table 1 lists some widely used coefficients and their formulae as extracted from [ 21]. Among all coefficients, Tanimoto has been proven to be the most effective [ 22] and is constantly used, especially for binary fingerprints, since it uses the ratio of the intersecting set (or overlapping set) to determine the similarity of the sets. In this work, we also adopt Tanimoto as our coefficient.
2.4 Similarity Searching
Similarity searching is a process of finding compounds in a database similar to the compound being sought (query). Given a query compound, a search is conducted by calculating the similarity with each compound in the database. Fig. 2 illustrates the process on compounds represented by ECFC4 with similarity calculated by the Tanimoto coefficient. Once the search is finished, database compounds are ranked based on their similarity score. Similarity evaluation is performed by taking the top 1% of the ranked list and matching it against the known actives where a recall value is returned. Further details on recall can be found in [ 23]. We will not dwell much on the recall values because we are more interested in improving the timing of the searching process.
2.5 Group Fusion
The group fusion algorithm consists of two main phases: the SS phase and the fusion phase. The basic procedure for group fusion is shown below (in Fig. 3), where n different reference compounds are used to search a database containing N compounds. The set of results (score or rank lists) of similarity scores Si( r,dj) for each database compound dj are then combined into a set of lists by using a selected fusion rule and then sorted in decreasing order. The complexity of the algorithm can be seen clearly from this algorithm, and the program has ( n) 2 complexity on the similarity search stage and ( n) on the fusion stage. The use of the fusion rule is to combine the output result from the similarity stage (similarity searches through a database of textual documents) into a single list. A number of random n reference compounds are selected as queries that later will obtain n sets of similarity scores to be fused (combined). There are a number of fusion rules available, as listed in [ 24]. We list the CombMAX rule that is used in this work in Table 2. The overall group fusion process can be divided into three main stages as shown in Fig. 4:
Pre-processing: Reference compounds with queries and database compounds will be read and prepared before the start of the similarity search process. Similarity Search: Marks the start of the SS campaign where the similarity between reference compound and database compounds are calculated. The result is a set of score/rank lists. Fusion: All sets of lists (obtained from the SS campaign) are combined into a unified list by using a selected fusion rule.
3. Parallel Methods and Implementation
It is a rule of thumb in any parallel design that a program undergoing parallelization must be an optimized one. This section discusses the optimization of the sequential program and proceeds to a detailed discussion on parallel design and implementation of group fusion. The main theme for optimization is to improve the time performance (elapsed time) on each stage by implementing a minor optimization approach. This approach is intended to focus on external methods as optimizer such as compiler and code compounds. GCC optimizer is used to compile the optimized group fusion. The reason for using GCC optimizer is to obtain faster compact codes and efficient code that can optimize full usage of registers in the given architecture. There are 5 levels of optimizer options provided by GCC; “−O0”, “−O1”, “−O2”, “−O3” and “−Os” for this design, we used level 2 optimization, −O2. This level of GCC optimizer performs optimization that does not involve a space-speed tradeoff. We do not want to disturb and limit memory space since group fusion is an approach that uses large data (size of database) as knowledge, and each piece of data contains rich information (compound ID, fingerprints). This type of program needs more space for temporary memory space during run time; therefore, making full use of available space is beneficial to the program.
3.1 OpenMP Method
The parallel OpenMP design addressed two code sections for parallelization similarity search and fusion MAX stages. In the SS stage, the parallel part concentrated on the inner loop, while fusion MAX focused on the parallel reduction in the outer loop. Fig. 5 expressed the use of OpenMP pragma directives towards group fusion algorithm in both stages. A series of tests was conducted on the parallel OpenMP program in order to evaluate the strength of the parallelized code fragments (similarity search and fusion) with multicore CPU to perform faster computations. By evaluating and analyzing the results of this section, we could measure the performance of the parallel section with low cores in CPU. First the program was tested with 10 query compounds for evaluating general execution time. Later, 5 query datasets consisting of 50, 100, 150 and 200 query compounds each, fingerprinted in floating point vector, were tested on the parallel OpenMP for measuring scalability of the program with different sizes of query.
3.2 Parallel CUDA Method
One of the reasons for the CUDA programming language is to take advantage of GPU that is specialized for intensive computing and enabling highly parallel computation. Therefore, the GPU architecture design is devoted to data processing because the same program is executed for each element; therefore, lower requirements are used for flow control and high arithmetic intensity. CUDA organizes parallel computations by using the abstraction of threads, blocks and grids. Threads are organized by blocks. A block is executed by the multiprocessing unit.
A kernel in CUDA programming is an atomic function or lines of arithmetic operations that is called many times and performs a computation on each element of data in GPUs. To take advantage of GPU and CUDA, lightweight tasks are defined in the kernel. A CUDA kernel is identified by an identifier that instructs the CUDA compiler that the function should be run on the GPU. Functions can be called from the host (CPU). The other function qualifier denotes functions that can be called from other global or device functions but cannot be called from the host. A CUDA kernel must have void output; therefore, in order to get the result back from a device (GPU) to the host (CPU), the pointers input must be passed and overwritten. Indexing in CUDA is defined below:
Data are stored in GPU memory using row-major order indexing. This method is used for describing and storing multi-dimensional arrays in linear memory. It follows the matrix notation for indexing, as rows are represented by the first index of two-dimensional arrays while columns are represented by the second index. Indexing is critical in order to get through each element correctly. In addition, due to caching, the traversing performance of an array is usually faster when stored in a linear way [ 25]. Therefore, data storage will be based on row-major order with a matrix form of multi-dimensional arrays as shown in Fig. 6. To sequentially traverse to a specific element of storage linear offset is used. From the start of the elements to any given element of Storage[height][width] can then be defined as: The idea of parallelization in a many-core architecture is to define a lightweight task in order to process the data as input. To make use of a lightweight task, the program code must be analyzed to identify the code fragment that represents the lightweight task for processing. The SS phase is embarrassingly parallel in nature; hence, it is suitable for executing as a lightweight task. Therefore, GPU processors (or called stream processors) will execute the SS lightweight process (as kernel) for calculating similarity between query and database compounds as a single small process.
In the Fusion (MAX) stage, fusion is solved using reduction. Reduction can be performed for specified operations on-the-fly without requiring additional storage thereby increasing the speed of the program. Fusion (MAX) works by finding the maximum similarity scores from the list of SS results that depicted similarity of two chemical compounds. The screening process to query for compounds against the database compounds during the similarity search stage produced a set of scores lists of database compounds. Applying the reduction operation can regain and speedup the program by taking advantage of the many-cores architecture in GPU with optimized dependency. Fig. 7 shows the overall CUDA kernel design of group fusion. In CUDA-based fusion (MAX) kernel, we avoid performing reduction of the first set of similarity search results so that the reduction operation will start only when two lists of SS results are made available. Later, the maximum scores from the operation will be overwritten or updated on the first list, represented as a vector. Different implementations of group fusion programs are available on https://bitbucket.org/codeoctopus/groupfusion under branch Seq-stable, OpenMP and CUDA-stable. The overall CUDA implementation of our work is presented in a high-level view of parallelism flows as shown in Fig. 8. The program consists of host code and device code that runs on CPU and GPU, not as separate pieces of code but like a single program. The preprocessing phase runs on host code while the similarity searching and fusion phases run on device code. The steps for solving similarity searching with CUDA in parallel are described below (remember that host refers to the CPU system while device refers to GPU):
Initialize SS CUDA preprocessing phase (includes all variable definitions and memory allocations for CUDA components) in the host Copy the database compounds from host to device memory Copy multiple query structures into device (GPU) memory Launch SS CUDA kernel and start performing similarity searching in GPU
Based on Fig. 8, the procedure for solving the fusion phase with CUDA in parallel runs after the similarity searching phase is completed. This phase is a reduction problem where multiple data are being merged and combine into single unified data. The procedures for solving parallel reduction are described below:
Initialize the Fusion CUDA phase (includes all variable initialization and memory allocation for GPU) Regroup the sets of results (score/rank lists) into 2D arrays of row-major order data structures in linear memory Launch the Fusion CUDA kernel. Perform fusion with selected rules by combining the sets of lists into a unified list. Copy the result (unified list) from the device to the host (matrix storage).
The algorithms and program were tested on an MDDR database. As in OpenMP, a set of 10, 50, 100, 150 and 200 query compounds were taken randomly from the 5HT1A activity class for the search. The CUDA binary was compiled using GCC compiler 4.4.3 and NVIDIA CUDA compiler 4.2 in order to enable parallelism in the GPU. All tests were run on a GPGPU server (biruni.cs.usm.my) located at the School of Computer Sciences, Universiti Sains Malaysia. The Biruni server is equipped with 4 cores AMD Phenom II X4 810 processor, 4 GB of RAM, running on Linux machine Ubuntu 10.04.4 LTS. The server is equipped with Tesla C2050 GPU card and comes with compute capability 2.0.
4. Results and Discussion
The performance of the group fusion implementation on a parallel platform is measured by the execution time and speedup. Speedup is an evaluation of the parallel algorithm compared to the sequential version. Speedup generally ranges between 0 and p, where p is the number of processors. The speedup, Sp, formula is defined in Eq. (3). In this equation, Ts and Tp denote the time taken to execute sequential and parallel versions to completion. Speedup has a strong connection with scalability. The scalability of the parallel algorithm is defined as the ability to achieve performance proportional to the number of processors used (as more processors are used, performance continues to improve). Therefore, computing speed is a good way to measure how the algorithm or program scales as more processors are used. The remainder of this section discusses our findings. Note that we did not include accuracy as a performance measure since our investigation is looking into the time improvement without trading off accuracy. Hence the accuracy of the algorithms is similar to those reported in [ 26].
4.1 General Evaluation
Fig. 9 illustrated the comparison of the execution time between the sequential, parallel OpenMP and parallel CUDA, respectively. As shown, there were no changes in the pre-processing stage since the stage involved reading input (database and query structures) from text files. As expected, overall, the parallel CUDA outperformed both sequential and parallel OpenMP execution times with similar search and fusion stages. One of the reasons is that GPU and CUDA programming is purposely designed to suit each other. The parallel CUDA program executed with 102,540 (the number of database structures) threads simultaneously due to the high number of cores available (448 cores as we tested) in the GPU. The stages (both the similarity search performed in embarrassingly parallel and fusion MAX performed in parallel reduction) are specialized for an SIMD (single instruction multiple data) approach thus contributing to higher performance.
In comparing parallel OpenMP with parallel CUDA, there was slightly lower performance in parallel OpenMP in the similarity stages while in the fusion MAX stages execution was more significant comparing fusion MAX to parallel CUDA. One of the reasons is OpenMP was limited to physical CPU processors (equipped with 4 cores only) and in addition, OpenMP performed well in the embarrassingly parallel approach compared to parallel reduction. This is because the embarrassingly parallel approach involved straight-forward computation and parallel reduction involved shared memory while performing read-write operations. Although OpenMP can more easily express parallelism with pragmatic directives, there is not much control for a developer to perform optimization in the low levels. Other than compiler optimization (that is provided in the compiler during compilation), it relies on the complexity of the arithmetic operation involved and should be well optimized.
Based on Fig. 10, the speedup of parallel CUDA is reflected in the execution time in all given sizes of the query dataset. For instance, the speedup of parallel CUDA with the 10 query dataset is 10.07× faster than sequential implementation (with the same size of query dataset) while the corresponding parallel OpenMP is 2.30× faster. Most of the contribution to better performance and speedup of the parallel CUDA comes from the optimization in both CUDA kernel functions of similarity search and fusion MAX stages. The underlying lightweight tasks directly affected computation, while the threads were not overly used in order to reduce idle threads during execution.
4.2 Scalability Analysis
This section addresses the evaluation results and analysis of the parallel OpenMP and parallel CUDA. The main objective is to measure the scalability of both parallel designs. Note that the sequential version was not included and discussed since it was out of scope and not fair for comparison with the parallel approach and design goals.
Fig. 11 shows the overall comparison between two parallel designs; parallel OpenMP and parallel CUDA for the dataset of 10, 50, 100, 150 and 200 query structures. Both parallel designs were tested with different sizes of query dataset and the execution time and speedup were obtained. The experiment was repeated 5 times with each size of query datasets taken randomly from 5HT1A activity class compounds.
Overall, the parallel CUDA design outperformed OpenMP in execution time. Initially, the execution time of parallel CUDA stayed below 100 seconds, as we concluded that both similarity search and fusion MAX stages did benefit from the advantages of GPU with many cores while the parallel OpenMP approach only took up to 4 cores. We were not quite satisfied since the overall result (execution time) did not depict the reality of performance unless we looked deeply into the performance of different stages (similarity search and fusion MAX).
Figs. 12 and 13 illustrate both similarity search and fusion MAX stages on both parallel CUDA and OpenMP. As seen in Fig. 12 on similarity search, parallel CUDA slightly outperformed parallel OpenMP in execution times. At this stage (similarity search), the operation is straight-forward and embarrassingly parallel, and thus, we do not see much significance of parallel CUDA compared with parallel OpenMP. There was no dependency on each SS operation; therefore, this parallel section did let allow both CUDA (in GPU) and OpenMP (pragmatic directive) advantages. In Fig. 12, we see a significant result from parallel CUDA compared to parallel OpenMP in the fusion MAX stage. Note that parallel reduction was involved in this stage and performed 10× faster than OpenMP, which is 2× faster than a sequential program. The margin between both parallel CUDA and parallel OpenMP will be greater when the query dataset is increased. One of the reasons that contribute to better parallel CUDA were the maximum number of threads used and the well-optimized arithmetic operation of fusion MAX in the CUDA kernel. CUDA APIs provide more control to the developer to seek an optimization approach thus making it possible to reduce flow control instructions (if, for, while) in the kernel. Therefore, the most intensive workload can be concentrated specifically in this stage while using maximum threads available in the GPU.
4.3 Limitation of Parallel CUDA of Group Fusion
Despite the parallel CUDA approach taking advantage of the GPUs architecture, there are a few limitations that lead to performance loss during computation. One of the factors is the use of threads in CUDA. Generally, the number of threads in CUDA can be controlled (by a developer using CUDA APIs). If the number of threads invoked from the kernel exceed the number of threads required for computation of the task, the excess threads will become idle.
There was no mechanism or guideline on how to have flexible thread management that suits a particular task and solves a particular problem. This is because the program was made to suit certain tasks and problems and had been hard coded for specific optimization. Even though the parallel CUDA design lacked flexibility in terms of thread management, the specific optimization was applied in order for the CUDA kernel to make full use of available threads in GPU.
Second, the communication cost for copying data from the host to device and from device to host increase execution time. The parallel CUDA takes nearly 156 seconds to copy data from host to device and nearly 8 seconds to copy data (the result) from device to host. These figures actually were much higher compared to the execution time for launching CUDA kernels. GPU has dedicated memory that has 5× to 10× faster bandwidth of CPU memory. Thus, copying data from the host (in CPU memory) to device (GPU memory) involved the PCI-E bandwidth passing through the South Bridge chip and then through the specific PCI-E device attached to the GPU card. Once the data are on the GPU card, any copies are very fast. Typically, a low-end GPU CUDA-capable card has internal bandwidth of 30–50 Gb/s, while the actual achievable bandwidth over the PCI-E to main memory is less. Regardless, the bandwidth between GPU and CPU is hardware dependent and it is a matter of how much a developer could gauge and design with prior knowledge of the GPU architecture.
5. Conclusion
The performance issues of screening large database compounds and multiple query compounds in virtual screening are a wide concern in Chemoinformatics applications. This study investigates these problems by choosing group fusion as a pilot model and presents efficient parallel solution in multi-cores and many-cores architecture of GPU. The design involved solving two important stages of group fusion, SS and Fusion (MAX rule), while both addressed embarrassingly parallel and parallel reduction models.
In the stage of fusion MAX, the CUDA binary program had shown better results for execution time (0.0004 s), parallel OpenMP (51.8682 s) and optimized sequential (135.9141 s). In the stage of Similarity Search, CUDA had shown better result for execution time (1.5749 s), parallel OpenMP (2.2550 s) and optimized sequential (7.3474 s). The proposed parallel CUDA design also proved to be scalable as N size of query compounds that were used produced N times complexity towards large database compounds. One of the reasons that contributed to this effectiveness was the availability of many-cores in GPU. The parallel CUDA was 5–10× faster than sequential and parallel OpenMP as both similarity search and fusion MAX stages had been CUDA-optimized.
Biography
Muhammad-Norhadri Mohd-Hilmi
He received M.Sc. and B.Sc. (Hons) degrees in computer science from the Universiti Sains Malaysia, Penang Malaysia in 2013 and 2010, respectively. His current research interests include computational chemistry, high-performance computing, ITS (intelligent transportation systems), vehicular network application and, recently, machine learning.
Biography
Marwah Haitham Al-Laila
She completed her B.Sc. in Computer Science in Iraq. In 2013, she received her M.Sc. degree in computer science from Universiti Sains Malaysia, Penang, Malaysia. Her current research interests include high-performance computing and sentiment analysis. She is currently a PhD candidate in the School of Computer Sciences, Universiti Sains Malaysia.
Biography
Nurul Hashimah Ahamed Hassain Malim
She received her B.Sc. (Hons) in computer science and M.Sc. in computer science from Universiti Sains Malaysia, Malaysia. She completed her Ph.D. in 2011 from The University of Sheffield, UK. Her current research interests include high-performance computing, chemoinformatics, bioinformatics, data analytics and sentiment analysis. She is currently a Senior Lecturer in the School of Computer Sciences, Universiti Sains Malaysia, Penang, Malaysia.
References
1. J. Gasteiger, "Chemoinformatics: a new field with a long tradition," Analytical and Bioanalytical Chemistry, vol. 384, no. 1, pp. 57-64, 2006.  2. WP. Walters, MT. Stahl, and MA. Murcko, "Virtual screening: an overview," Drug Discovery Today, vol. 3, no. 4, pp. 160-178, 1998.  3. P. Willett, JM. Barnard, and GM. Downs, "Chemical similarity searching," Journal of Chemical Information and Computer Sciences, vol. 38, no. 6, pp. 983-996, 1998.  4. J. Hert, P. Willett, DJ. Wilton, P. Acklin, K. Azzaoui, E. Jacoby, and A. Schuffenhauer, "Enhancing the effectiveness of similarity-based virtual screening using nearest-neighbor information," Journal of Medicinal Chemistry, vol. 48, no. 22, pp. 7049-7054, 2005.  5. P. Willett, "Combination of similarity rankings using data fusion," Journal of Chemical Information and Modeling, vol. 53, no. 1, pp. 1-10, 2013.  6. J. Hert, P. Willett, DJ. Wilton, P. Acklin, K. Azzaoui, E. Jacoby, and A. Schuffenhauer, "Comparison of fingerprint-based methods for virtual screening using multiple bioactive reference structures," Journal of Chemical Information and Computer Sciences, vol. 44, no. 3, pp. 1177-1185, 2004.  7. M. Whittle, VJ. Gillet, P. Willett, A. Alex, and J. Loesel, "Enhancing the effectiveness of virtual screening by fusing nearest neighbor lists: a comparison of similarity coefficients," Journal of Chemical Information and Computer Sciences, vol. 44, no. 5, pp. 1840-1848, 2004.  8. M. Vogt, and J. Bajorath, "Chemoinformatics: a view of the field and current trends in method development," Bioorganic & Medicinal Chemistry, vol. 20, no. 18, pp. 5317-5323, 2012.  9. I. Sanchez-Linares, H. Perez-Sanchez, and JM. Garcia, "Accelerating grid kernels for virtual screening on graphics processing units," in Applications, Tools, and Techniques on the Road to Exascale Computing, Amsterdam: IOS Press, 2001, pp. 413-420.
10. M. Maggioni, MD. Santambrogio, and J. Liang, "GPU-accelerated chemical similarity assessment for large scale databases," Procedia Computer Science, vol. 4, pp. 2007-2016, 2011.  11. R. Lambert, "An introduction to Derwent World Drug Index," in EuroMug 2000, Cambridge, UK, 2000.
12. DS. Wishart, C. Knox, AC. Guo, S. Shrivastava, M. Hassanali, P. Stothard, Z. Chang, and J. Woolsey, "DrugBank: a comprehensive resource for in silico drug discovery and exploration," Nucleic Acids Research, vol. 34, no. Suppl 1, pp. D668-D672, 2006.  13. C. Southan, P. Várkonyi, and S. Muresan, "Quantitative assessment of the expanding complementarity between public and commercial databases of bioactive compounds," Journal of Cheminformatics, vol. 1, article no. 10, 2009.  14. SO. Jonsdottir, FS. J⊘rgensen, and S. Brunak, "Prediction methods and databases within chemoinformatics: emphasis on drugs and drug candidates," Bioinformatics, vol. 21, no. 10, pp. 2145-2160, 2005.  15. J. Gasteiger, and T. Engel, in Chemoinformatics: A Textbook, Weinheim: Wiley-VCH, 2003.
16. P. Willett, "Similarity-based virtual screening using 2D fingerprints," Drug Discovery Today, vol. 11, no. 23, pp. 1046-1053, 2006.  17. D. Rogers, and M. Hahn, "Extended-connectivity fingerprints," Journal of Chemical Information and Modeling, vol. 50, no. 5, pp. 742-754, 2010.  18. M. Hassan, RD. Brown, S. Varma-O’Brien, and D. Rogers, "Cheminformatics analysis and learning in a data pipelining environment," Molecular Diversity, vol. 10, no. 3, pp. 283-299, 2006.  19. N. Salim, J. Holliday, and P. Willett, "Combination of fingerprint-based similarity coefficients using data fusion," Journal of Chemical Information and Computer Sciences, vol. 43, no. 2, pp. 435-442, 2003.  20. PH. Sneath, and RR. Sokal, in Numerical Taxonomy: The Principles and Practice of Numerical Classification, San Francisco, CA: W. H. Freeman, 1973.
21. AR. Leach, and VJ. Gillet, in An Introduction to Chemoinformatics, Dordrecht: Springer, 2007.
22. D. Bajusz, A. Rácz, and K. Héberger, "Why is Tanimoto index an appropriate choice for fingerprint-based similarity calculations?," Journal of Cheminformatics, vol. 7, article no. 20, 2015.  23. N. Malim, Y. Pei-Chia, and SM. Arif, "New strategy for turbo similarity searching: implementation and testing," in Proceedings of 2013 International Conference on Advanced Computer Science and Information Systems (ICACSIS), Bali, Indonesia, 2013, pp. 179-184.  24. AA. Zainal, N. Yusri, N. Malim, and SM. Arif, "The influence of similarity measures and fusion rules toward turbo similarity searching," Procedia Technology, vol. 11, pp. 823-833, 2013.  25. EJ. Otoo, and D. Rotem, "Parallel access of out-of-core dense extendible arrays," in Proceedings of 2007 IEEE International Conference on Cluster Computing, Austin, TX, 2007, pp. 31-40.  26. N. Malim, "Enhancing similarity searching,"PhD dissertation, University of Sheffield; UK: 2011.
Fig. 1
Example of chemical compound R represented in a 2D-chemical diagram encoded into SMILES, ECFP, and ECFC fingerprints. 
Fig. 2
Illustration of similarity search using ECFP4 and Tanimoto. 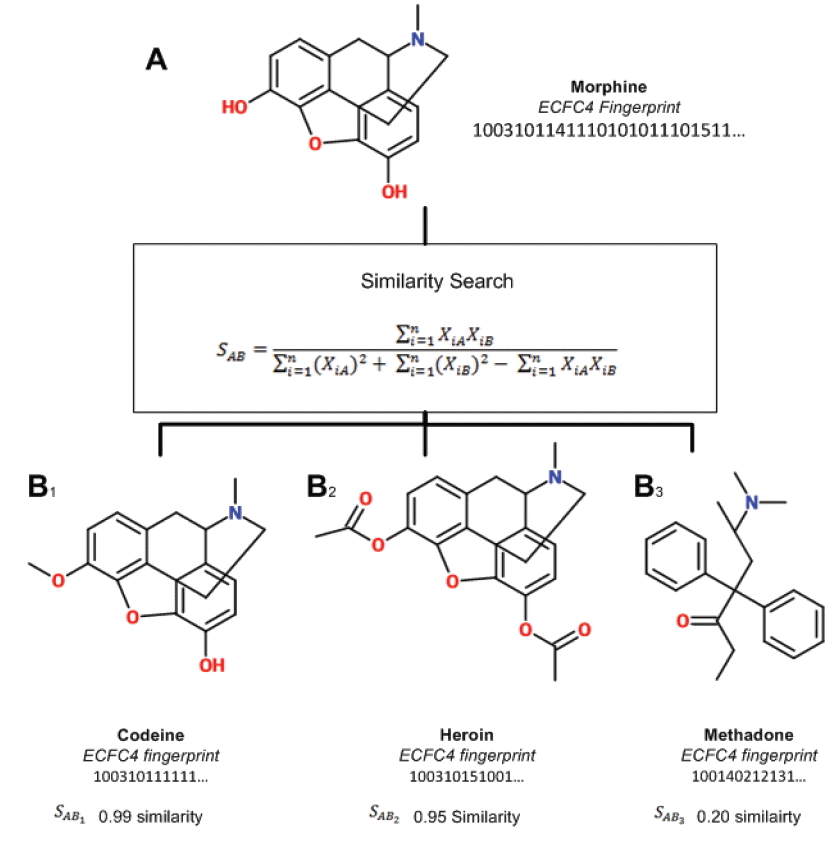
Fig. 3

Fig. 4
High-level architecture of group fusion. 
Fig. 5
Placement of pragma omp directives on similarity search and fusion MAX. 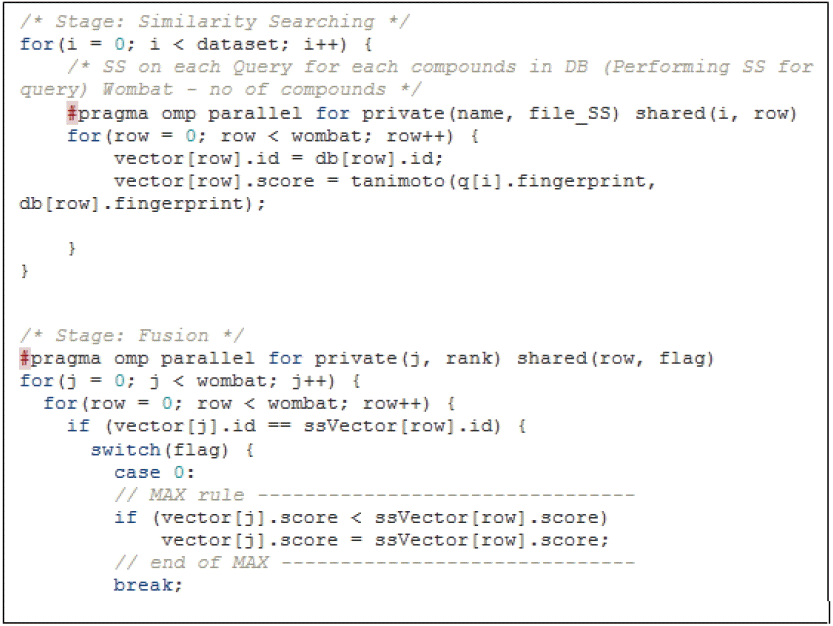
Fig. 6

Fig. 7
Illustration of CUDA kernel design of group fusion. 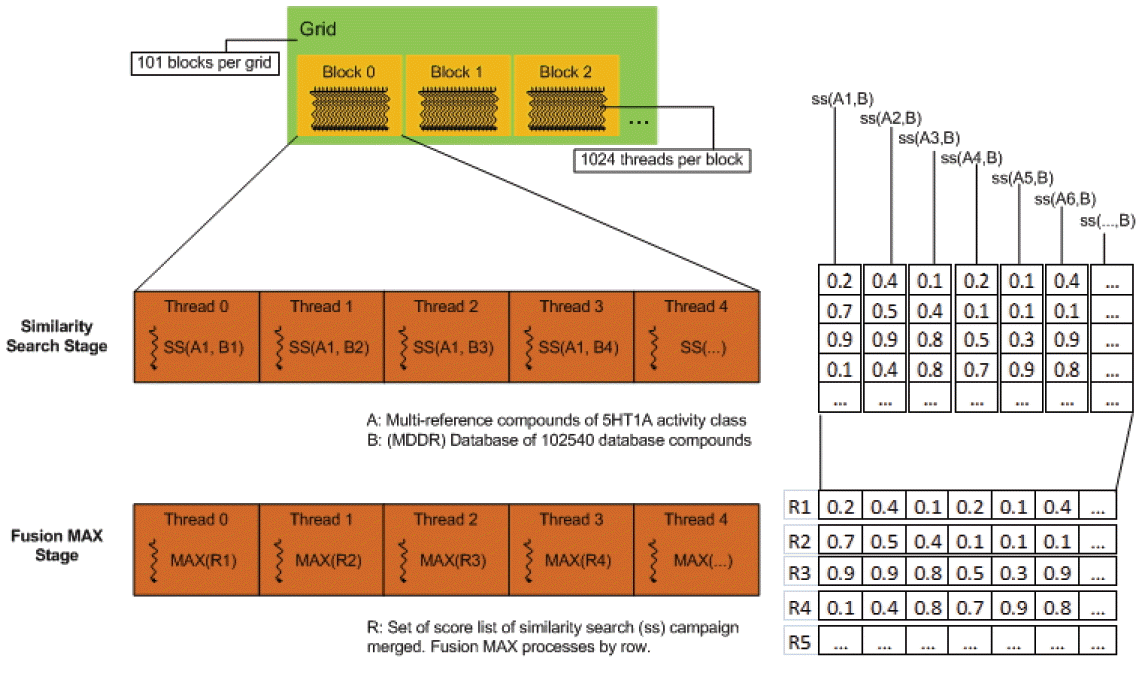
Fig. 8
Overall proposed CUDA design of group fusion. 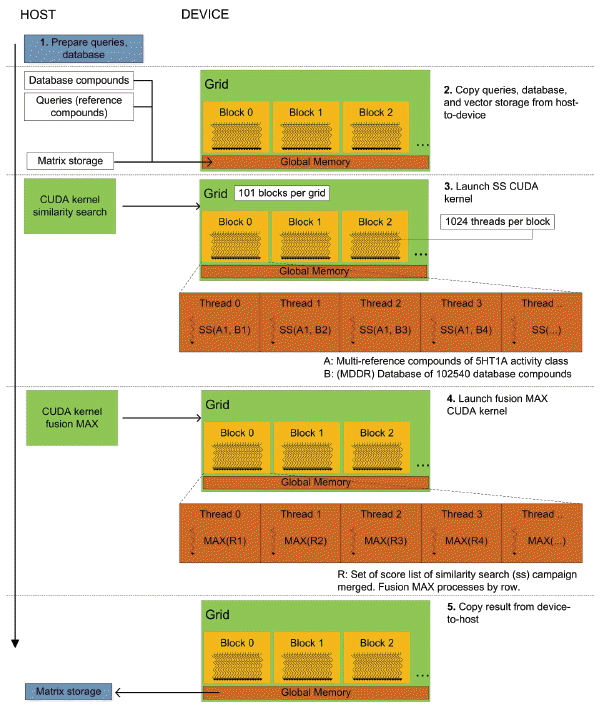
Fig. 9
Comparison of sequential, parallel OpenMP and parallel CUDA for 10 query compounds. 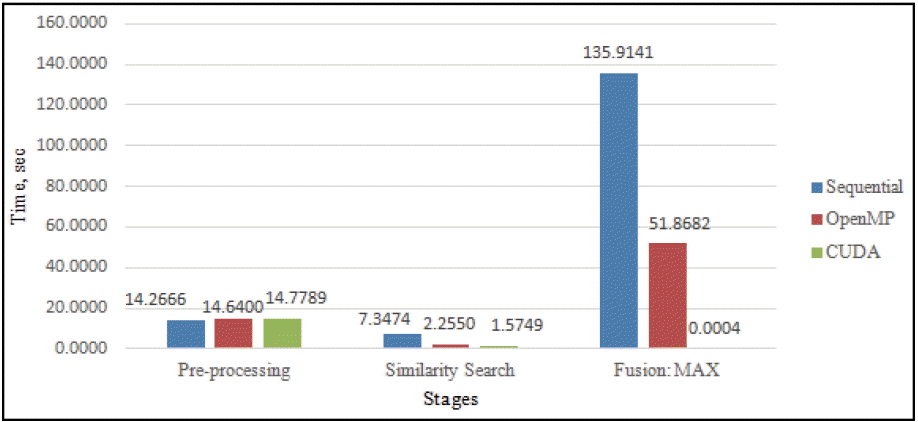
Fig. 10
Comparison of speedup between parallel OpenMP and parallel CUDA. 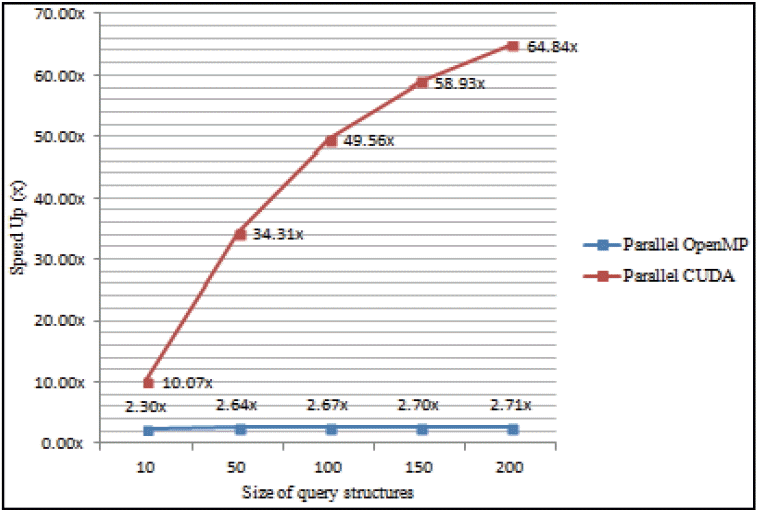
Fig. 11
Comparison between OpenMP and CUDA on execution time. 
Fig. 12
Comparison between OpenMP and CUDA of similarity search stage. 
Fig. 13
Comparison between OpenMP and CUDA of fusion MAX stage. 
Table 1
Some of association ( S) and distance ( D) coefficients [ 21]
|
Name |
Formula for continous variables (floating point vector) |
Formula for binary (dichotomous) variables |
|
Tanimoto coefficient |
SAB=∑i=1NXiAXiB∑i=1N(XiA)2+∑i=1N(XiB)2-∑i=1NXiAXiB
Range: −0.333 to + 1 |
SAB=ca+b-c
Range: 0 to 1 |
|
Dice coefficient |
SAB=2∑i=1NXiAXiB∑i=1N(XiA)2+∑i=1N(XiB)2
Range: −1 to + 1 |
SAB=2ca+b
Range: 0 to 1 |
|
Cosine similarity |
SAB=∑i=1NXiAXiB[∑i=1N(XiA)2∑i=1N(XiB)2]1/2
Range: −1 to + 1 |
SAB=cab
Range: 0 to 1 |
|
Euclidean distance |
DAB=[∑i=1N(XiA-XiB)2]1/2
Range: 0 to ∞ |
DAR=a+b-2c
Range: 0 to N |
|
Soergel distance |
DAB=∑i=1N|XiAXiB|∑i=1Nmax (XiA,XiB)
Range: 0 to 1 |
DAB=a+b-2ca+b-c
Range: 0 to 1 |
Table 2
Fusion rules used in this work
|
Fusion rule |
Formula |
|
CombMAX (MAX) |
SMAX (dj) = max{S1(dj),S2(dj),...Si(dj),...Sn(dj)} |
|















