Byun and Jang: A Column-Aware Index Management Using Flash Memory for Read-Intensive Databases
Abstract
Most traditional database systems exploit a record-oriented model where the attributes of a record are placed contiguously in a hard disk to achieve high performance writes. However, for read-mostly data warehouse systems, the column-oriented database has become a proper model because of its superior read performance. Today, flash memory is largely recognized as the preferred storage media for high-speed database systems. In this paper, we introduce a column-oriented database model based on flash memory and then propose a new column-aware flash indexing scheme for the high-speed column-oriented data warehouse systems. Our index management scheme, which uses an enhanced B+-Tree, achieves superior search performance by indexing an embedded segment and packing an unused space in internal and leaf nodes. Based on the performance results of two test databases, we concluded that the column-aware flash index management outperforms the traditional scheme in the respect of the mixed operation throughput and its response time.
Key words: Column-Aware Index Management, Column-Oriented Databases, Flash Memory Storage, Game Database, Network Database
1. Introduction
Traditional database management systems are based on record-oriented storage systems, where the attributes of a record are placed contiguously in storage. With this row store architecture, a single disk write suffices to push all of the fields of a single record out to the disk. Hence, high performance writes are achieved and these write-optimized systems are especially effective on online transaction processing (OLTP) style applications [ 1]. In contrast, systems oriented toward the ad-hoc querying of large amounts of data should be read-optimized. Data warehouses represent one well-known class of read-optimized systems, in which a bulk load of new data is periodically performed, followed by a relatively long period of ad-hoc queries. Other read-mostly applications include customer relationship management (CRM) systems, electronic library card catalogs, and other ad-hoc inquiry systems. In such environments, a column store architecture, in which the values for each single column are stored contiguously, should be more efficient. This efficiency has been demonstrated in the data warehouse marketplace by products like Sybase IQ [ 2]. With column store architecture, a DBMS only needs to read the values of columns required for processing a given query, and it can avoid bringing in memory irrelevant attributes. In data warehouse environments where typical queries involve aggregates performed over large numbers of data items, a column store has a sizeable performance advantage [ 1, 3]. Column-oriented databases, as well as general record-oriented databases, were designed to store data items in hard disks in the past. However, recent flash memory storage, called solid state drive (SSD), has become a critical component in building high-performance servers because of its superior I/O performance, being non-volatile, shock-resistant, and having a power-economic nature. Its storage density has been improved to a level at which it can be used not only as a main storage for portable computers, but also as a mass storage for large-volume database systems [ 4]. The contributions of this paper are as follows:
We investigate the characteristics of the column-oriented database and flash memory storage for read-intensive data warehouse servers. We propose a new index management scheme, called column-aware flash memory-based index (CaF index), to improve the performance of search operations for a column-oriented database system using flash memory storage. Finally, we evaluate the performance of our scheme in terms of the search and update operation throughput and the average response time.
2. Related Work
2.1 Characteristics of Flash Memory
Similar to a lot of storage media, flash memories are treated as ordinary block-oriented storage media, and file systems are built over flash memories. A flash memory consists of many blocks, and each page consists of a fixed number of pages. In Fig. 1, the size of the page and the block size of a flash memory are 4 kB and 256 KB, respectively. Because flash memory is write-once, we did not overwrite data with updates. Instead, the data was written in a free space, and the old versions were invalidated. Initially, all blocks on the flash memory are considered free. When a piece of data on a block is modified, the new version must be written somewhere on an available block. The blocks storing the old versions are considered dead, while the block storing the newest version is considered to be alive. After a certain period of time, the number of free blocks is reduced. As a result, the system must reclaim free blocks for further writes. The slow erase operation contributes to degrading the system’s performance [ 5]. Flash memory has two drawbacks. First, the blocks of flash memory need to be erased before they can be rewritten. This drawback is caused by the fact that flash memory technology allows the toggling of individual bits for writes in only one way. The erase operation, which needs much more time than the read or write operations, resets the memory cells with either all ones or all zeros. The second drawback is that the number of rewrite operations allowed for each memory block is limited to fewer than 1,000,000. This limit requires the flash management system to wear down all memory blocks, as evenly as possible [ 6]. Note that flash memory is about two times faster than a hard disk with regards to the update operation, although flash memory has the characteristics of slow erase and writes. Moreover, flash memory is about four times faster than a hard disk with regards to the read operation. In this respect, we claim that the combination of flash memory storage and column-oriented database could establish a new high-performance database platform suited for large-volume data access, such as a read-intensive data warehouse.
2.2 Characteristics of Column-Oriented Databases
There are limits to the performance that row-oriented systems can deliver when tasked with a large number of simultaneous, diverse queries since they should read a lot of irrelevant attributes. In contrast, with column-oriented systems, only the columns used in a query need to be fetched from storage. In a column-oriented database, each column is stored contiguously on a separate location on disk, typically using large disk pages or large read units to amortize disk head seeks when scanning multiple columns on hard drives. To improve read efficiency, columnar values are typically densely packed, foregoing the explicit storage of record IDs, and using lightweight compression schemes [ 1, 4]. Especially, a column-oriented database facilitates vast improvements in compression, which can result in an additional reduction in storage access while maintaining high performance. One example, typically employed where a column contains often-repeating values, involves tokenizing the commonly used data values and mapping those values to tokens that are stored for each row in the column. For example, instead of maintaining copies of city name values in address records, each city name, such as ‘Los Angeles,’ can be mapped to an integer value such as 1,397, which requires 2-bytes to store, rather than 11-bytes. The resulting compression is five times in this example. As another example, run length encoding is a technique that represents runs of data using counts, and this can be used to reduce the space needs for columns that maintain a limited set of values, such as flags or codes [ 3]. As compared to a simple row-oriented database, the disadvantage of column-oriented database is tuple construction overhead. This is because a column-oriented database should reconstruct partial or entire tuples (records) out of different columns in disk for most database access standards (e.g., ODBC and JDBC). However, this overhead can be mitigated by some techniques, such as in-memory buffering, tuple moving, and partition-merging. Furthermore, in the respect of computational efficiency of pipelined query or vectorized query processing, a column-oriented database is much more suitable to exploit the features of modern processors, such as pipelined CPUs, CPU branch prediction, CPU cache efficiency, and SIMD instructions [ 1]. For example, the MonetDB/X100 systems that pioneered the design of modern column-oriented database systems and vectorized query execution show that column-oriented database designs can dramatically outperform commercial and open source databases on benchmarks like TPC-H due to superior CPU and cache performance, in addition to reduced data I/O [ 7].
2.3 Characteristics of Traditional Index Management Schemes
Previous approaches to dealing with indexing techniques that appear in [ 6] can be divided into two categories: hard disk-based and main memory-based approaches. The hard disk-based approach achieves high index performance by reducing expensive disk I/O and disk space. The cost of slow disk access is much more expensive than that of fast CPU access in the course of an index search. Therefore, in order to optimize disk access, a disk-based system sets the index node size to the block size and includes as many entries as possible in a node [ 8]. Two well-known index structures are B-Tree for a general index and R-Tree for a spatial index [ 9]. R-Tree is usually implemented as a disk-based index structure for accessing a large collection of spatial data. Insertion, deletion, and re-balancing often cause many sectors to be read and written back to the same locations. For disk storage systems, these operations are considered efficient, and R-Tree nodes are usually grouped in contiguous sectors on a disk for further efficiency considerations [ 10]. The memory-based index aims to reduce CPU execution time and memory space since there is no disk I/O. In general, the memory-based indexing system outperforms the disk-based system in terms of index operation performance. However, the memory-based systems could suffer from unreliable data access due to system faults, such as a power failure. The well-known index structure for a memory-based system is T-Tree [ 11]. T-Tree has the characteristics of the AVL-Tree, which has O(logN) tree traverse. T-Tree also has the characteristics of B-Tree, which has many entries in a node for space-efficiency. T-Tree is considered a good structure for a memory-based index in terms of index operation performance and space efficiency [ 12]. However, in [ 11], the performance of the B-Tree could outperform that of the T-Tree due to the concurrency control overhead. Thus, for performance reasons, a memory-based system generally uses enhanced B-Trees as well as T-Trees. In disk-based systems, each node block may contain a large number of keys. The number of subtrees in each node, then, may also be large. The B-Tree is designed to branch out in a large number of directions and to contain a lot of keys in each node so that the height of the tree is relatively small. This means that only a small number of nodes must be read from the disk to retrieve an item. The goal is to have quick access to the data, and this means reading a very small number of records [ 13]. That is, the depth of the tree is very important because the number of node accesses refers to the number of disk I/O in the course of the tree traverse to search for or insert a node. Thus, the disk-based system minimizes the disk I/O cost by using a shallow and broad tree index. The memory-based system, on the other hand, does not prefer a shallow and broad tree index. This is because the depth of the tree or the size of the tree node can be adjusted to improve index performance, and the node access cost is very low in a fast RAM. Unfortunately, index design and the implementation of a disk-based or memory-based system could not be applied directly to a flash memory-based due to the unique characteristics of flash memory. First, the fast read operation should be exploited more frequently and more efficiently than the slow write and erase operations, especially in search-intensive systems such as read-mostly data warehouses. Second, for the longer lifetime of the flash memory, the number of write operations should be minimized in the index node update processes [ 14]. For these reasons, any direct application of the traditional index implementation to flash memory could result in severe performance degradation, and could reduce its reliability. However, if these special features are handled efficiently, the flash memory is considered as the most affordable storage media for read-intensive applications, especially for column-oriented databases.
3. Column-Aware Index Management Using Flash Memory
In order to devise a new index management scheme for a column-oriented database using flash memory, we focused on a B-Tree-based index, especially the B+-Tree, which is considered to be the most well-known and efficient indexing scheme for both disk-based and memory-based database systems. The B+-Tree is an enhanced index of the B-Tree and is considered to be more suitable than B-Tree for flash memory. This is because B+-Tree stores index entries in internal nodes, and data entries in leaf nodes. On the other hand, B-Tree stores both index and data entries in internal nodes. Thus, B+-Tree is able to search more quickly with less I/O than B-Tree. In this respect, we proposed a new index management structure called the CaF index, which is based on the B+-Tree and is able to efficiently handle the characteristics of flash memories and column-oriented database. The main idea behind the CaF index is based on unused space packing and the embedded segment index.
3.1 The Idea of the Column-Aware Flash Index Management
The B +-Tree is a well-known index tree designed for efficient index operations, such as insertion, deletion, and search. The idea behind B +-Trees is that internal nodes can have a variable number of child nodes within some pre-defined range. As data is inserted or removed from the data structure, the number of child nodes varies within a node, and so the internal nodes are coalesced or split so as to maintain the designed range. Because a range of child nodes is permitted, B +-Trees do not need re-balancing as frequently as other self-balancing binary search trees, but may waste some space since the nodes are not entirely full. The lower and upper bounds on the number of child nodes are typically fixed for a particular implementation [ 15]. The B +-Tree is kept balanced by requiring that all leaf nodes have the same depth. This depth will increase slowly as elements are added to the tree, but an increase in the overall depth is infrequent, resulting in all leaf nodes being one more hop further removed from the root. By maximizing the number of child nodes within each internal node, the height of the tree decreases, balancing occurs less often, and efficiency increases. In [ 9], the simulation shows that the average fill factor of about 70% is the most optimal value in a B +-Tree node. That is, saving too many entries in a node could lead to performance degradation due to frequent insert/delete operations caused by tree rebalancing. However, from the point of flash memory, 30% of the unused area is a waste of space and time. This is because flash memory is write-once so that it cannot overwrite in the same block. Instead, updated data is written in a new free block. In this respect, we exploited unused space packing so that the column-oriented database storage removes unnecessary space overhead and a meaningless writing time of blank data. As illustrated in Figs. 2 and 3, the unused area of the B +-Tree node could be saved by up to 30% in the CaF index scheme. Unlike the general row-oriented databases, column-oriented databases exploit data compression to save flash memory and to accelerate data access. Since the column-oriented database handles mostly read-intensive data warehouses, the column-oriented database should manage big data access and a frequent uncompression process. Thus, the longer the data is, the more time it consumes in the uncompression process.
In order to reduce this uncompression overhead and achieve fast data access, the CaF index exploits embedded segment indexing in the leaf node, as illustrated in Fig. 2. Unlike the general index scheme, such as B-Tree, embedded segment indexing splits large data into small data units called an embedded segment. The compression and uncompression overhead of the small segment is naturally lessened as compared to original large data. The key and the segment offset of each small segment are kept in the header area of the embedded segment index in the leaf node. Since the CaF index can jump to the start position of the target segment and can uncompress only the small segment, which contains the key, the data search performance is significantly improved as compared to the case of entirely uncompressing one large data.
We used a real-time data compression library called LZO [ 16], for the node compression in a sense that LZO is not only simple but also easy for handling source codes and varying the compression level to control the compression ratio and speed. In Fig. 2, the original leaf node consists of a long header and large data compressed by the LZO algorithm. We split this original node into multiple small segment arrays, which consist of compression header i, denoted by h i, and compressed data, denoted by d i. Each h i consists of several pieces of format information, such as the LZO signature, current compression version, last modification time, crc-32 checksum, and the compressed byte size of input data. Each d i contains output data compressed by the LZO algorithm. Note that the output data size is much smaller than the data size of the original node. This embedded segmentation contributes to reducing the leaf node access time by exploiting the small segment index. In order to improve the index operation performance of the B-Tree for flash memory storage, some index structures, such as the FD-Tree [ 17] and BFTL [ 18], were proposed. The FD-Tree was designed with the logarithmic method and fractional cascading techniques. With the logarithmic method, an FD-Tree consists of the head tree - a small B +-Tree on the top, and a few levels of sorted runs of increasing sizes at the bottom ( Fig. 4). With the fractional cascading technique, FD-Tree store pointers, called fences, in lower level runs to speed up the search. FD-Tree design is mainly write-optimized for the flash memory. In particular, an index search will potentially go through more levels or visit more nodes, but random writes are limited to a small head tree. Although both the FD-Tree and our scheme improve index operation performances, the focus of our scheme is different from that of the FD-Tree, which is optimized to reduce the number of write operations in the B-Tree. The first difference is that our scheme is chiefly a read-optimized method for read-intensive data warehouses. The second difference is that our major modification is on leaf nodes, while the FD-Tree scheme modified root and internal nodes to enhance read performance.
BFTL could efficiently handle fine-grained updates caused by B-Tree index access and reduce the number of redundant write operations in flash memory. BFTL consists of a small reservation buffer and a node translation table. When the applications insert or delete records, the newly generated records would be temporarily held by the reservation buffer to reduce redundant writes. Since the reservation buffer only holds an adequate amount of records, the index unit of the records should be flushed in a timely manner to the flash memory. The node translation table maintains the logical sector addresses of the index units of the B-Tree node so that the collection of the index units could be more efficient by smartly packing them into a few sectors. Although BFTL achieves an enhanced performance in terms of write operations, it requires an additional hardware implementation of the reservation buffer and the node translation table. Furthermore, the search overhead can increase with frequent access to the reservation buffer and the node translation table.
The focus of our scheme is different from that of BFTL. That is, BFTL aims to minimize redundant writes by using an additional hardware buffer in the B-Tree, while our scheme aims to enhance read operations by index segmentation and unused space packing techniques. Moreover, in the respect of write operation, our scheme exploits leaf node compression, while BFTL exploits the delayed writing technique. Therefore, the different features of our scheme and BFTL can be merged to maximize performance synergy in flash memory storage systems.
Our CaF index structure and the proposed algorithm are also applicable to row-oriented databases. Moreover, flash memory could double row-oriented database performance, especially in read-intensive data warehouse areas. However, our scheme is optimized for column-oriented databases rather than row-oriented databases. This is because column-oriented databases are considerably compressed and have column-wise locality since column data are serially stored in the same field.
Note that the row-oriented database has a weaker locality than the column-oriented database and thus should access many more pages since a row-oriented database is not compressed as much as a column-oriented database. The CaF index scheme exploits this column-wise locality so that database system enhances I/O performance and space efficiency in expensive flash storages. Moreover, if the CaF index scheme selects a different compression algorithm in each column characteristic, such as the number, Boolean, and string, column-oriented database performance would be upgraded.
3.2 Algorithms for CaF Index Operation
The search operation of the CaF index scheme is based on well-known B +-Tree management algorithms in [ 9], but is modified to include an embedded segment uncompression idea. The detailed procedure of handling index operations can be shown in a pseudo-code form as Algorithm 3.1. Our CaF tree, as well as the B+-Tree, consists of a root, internal nodes, and leaf nodes. The search operation to find a key in the CaF tree always follows one path from the root node, denoted by R, to a leaf node. This search algorithm can be illustrated as explained below.
Example 3.1
(Search Procedure of the CaF Index Scheme):
Consider that we are looking for corresponding data to key value, 37, in the CaF tree ( Fig. 5). Suppose that there are two key values, { 30, 50}, in the internal node, denoted by node-a, for simplicity. At the node-a, the CaF index search algorithm figures out which internal pointer it should follow. Since with the search key, x=37 and 30< x ≤50, it should follow node-c. It then selects the second pointer, p2, in the leaf node-c and finds the corresponding data space.
It then creates a temp space T in RAM for fast uncompression, after which it calculates a corresponding segment distance, denoted by SegmentOffset for the key, 37. By accessing the embedded segment index, denoted by seg[], the search operation can avoid the uncompression overhead of Segment1 and can move the input pointer to Segment2. It then only reads the Segment2 area in flash memory by invoking FM-Read() and uncompresses only Segment2 into T by invoking the Lzo_Uncompress_Segment(). And then, it returns the target data, Di, such that key=37, in T.
4. Results
We compared the performance of three types of the CaF tree to the well-known index, B +-Tree. The average fill factor of the B +-Tree was fixed to 70%, which is a basic value for the best performance [ 9]. We denote these basic B +-Trees as BT_BAS, shortly in our test . As mentioned above, our CaF index scheme exploits empty space packing in internal and leaf nodes for space-efficiency. We denote this type of CaF tree as CT_PACK. Our CaF index scheme also exploits embedded segment compression in leaf nodes for search-efficiency. We denote this type of CaF tree as CT_EMB. Finally, we also denote the type of CaF tree, which exploits both CT_EMB and CT_PACK for the best performance as CT_EaP.
4.1 Test Environment Setup
Our system was programmed using Microsoft Visual C++ and the CSIM library [ 19] for workload generation and performance analysis. Our actual experiments were carried out on an I7-QUAD 2.93 GHz server with 120 GB flash memory SSD running under a 64-bit Microsoft Windows 7 operating system. We also obtained two types of real databases, which are frequently used in a game portal and a network company, and expanded them to ten million records for a large database organization. The game database in Table 1, denoted by TestSet1, is used to analyze search and update queries under a normal workload condition. The network database in Table 2, denoted by TestSet2, is used to analyze a mixed query, which consists of 75% of the search operation and 25% of the update operation, under a high workload condition. The column characteristics of the two databases are as listed below. As mentioned above, we used the LZO algorithm for column data compression, and our compression test showed that the compressed data ratio is less than 8% in TestSet1, less than 10% in TestSet2, respectively. Due to the high data locality feature of column-oriented databases, the compression result is very positive, especially for text, Boolean, or code data compression, such as GameCheat Flag and GameCode. The compressed set size of 10,000 records is less than 14 kB in TestSet1 and less than 33 kB in TestSet2, respectively. The CSIM workload generator randomly selects the columns associated with queries.
The primary performance metrics used in this study are the column operation throughput rate and the response time. The throughput rate is defined as the number of column searches or update operations that are successfully completed per second, and the response time is defined as the time that elapses between the submission and the completion of the column operation.
4.2 Test Results and Their Interpretation
We then analyzed the results of the experiments performed for the four schemes of BT_BAS, CT_PACK, CT_EMB, and CT_EaP. Our experiments were used to investigate the effect of the column search workload level on the performance of four schemes in which the num_CSRs and the number of column search requests per second varies.
The overall search throughput as a function of num_CSRs is presented in Fig. 6, and its corresponding average response time is depicted in Fig. 7. In Fig. 6, the x-axis means the input workload, which is the number of submitted search operations per second. Thus, varying the number of issued search operations means the variation of the database system workload. The y-axis means the output performance, which is the number of completed search operations per second. In Fig. 7, the average response time gradually increases with the workload level. This increase is mainly due to the increment of the search access contention that follows the increment of the workload level. In this experiment, we observed that CT_EaP, followed by CT_EMB, CT_PACK, and BT_BAS, exhibits the highest throughput. In Fig. 6, we show that the performance of each scheme levels off or begins to be degraded beyond the num_CSRs of 500 to 700. Although the num_CSRs has been increased beyond that range, the number of active search operations that are currently being executed in the database system appears to decrease slightly. This fact implies that adding more search operations beyond that range simply contributes to increasing the search I/O contention, while not necessarily incurring an enhanced level of throughput. From this observation, we can claim that the performances of the column-oriented database storages are mainly limited by the factor of I/O contentions, such as uncompression and read operations, caused by flash memory search procedures. In Fig. 7, we show that the performance of CT_EaP begins to decrease as the num_CSRs increases beyond 700, although CT_EaP achieves higher performance than BT_BAS by reducing the congested search operations of flash memory using embedded segment indexing and empty space packing. This decrease implies that CT_EaP also experiences the negative effect of search contention under the high workload environment. CT_EMB shows slightly higher performance than CT_PACK in a high workload environment. This is because CT_EMB effectively reduces the degree of the uncompression workload by using the embedded segment indexing. In Fig. 7, we observed that the response time of each scheme increases gradually as the workload level increases. At the overall workload level, the response curve of CT_EaP is superior to that of BT_BAS. With respect to the search operation throughput, the performance gain of CT_EaP relative to BT_BAS reaches about 17%. With respect to the search response time, the gain of CT_EaP relative to BT_BAS reaches about 34%. This performance difference implies that a large portion of the performance gain in CT_EaP over BT_BAS comes from the implementation of column-aware flash indexing to minimize search I/O overhead. However, BT_BAS scheme meaninglessly fetches the empty area of 30% of the flash memory space and this leads to requiring more I/O access to find the key and data in the B+-Tree. This is because the B+-Tree maintains the average fill factor of 70%, which was designed to reduce the number of times frequent tree rebalancing must be carried out in a slow hard disk environment.
On the contrary, in a fast flash memory environment, this fill factor feature of the B+-Tree generates more I/O accesses and a bigger uncompression workload. Eventually, this feature contributes to the severe performance degradation of BT_BAS due to the long I/O delay of flash memory and unnecessary uncompression overhead of the CPU, especially in a high workload condition. Compared to BT_BAS, CT_EaP successfully overcomes the negative effect of this overhead and enhances search speed by packing 30% of the useless area and inserting more internal nodes in the area under the same condition.
This assertion can be confirmed by comparing the number of waiting operations, queue-lengths, in Fig. 8. Actually, the sudden congestion of search operations begins at a queue-length of about 600 in our experiment. However, the number of waiting operations for column searches is always much lower using CT_EaP than using the other schemes. This is due to the positive effect of exploiting empty space packing in CT_EaP. Furthermore, CT_EaP exploits the embedded segment indexing to lessen this uncompression overhead and achieve fast data access in the leaf node. CT_EaP only uncompresses the small segment that contains the key rather than one piece of large data entirely. As a result, CT_EaP shows a 43% lower Queue-Length than BT_BAS throughout the whole range of num_CSRs. We also investigate the performance differences of four schemes in terms of column update operations. The update operation throughput as a function of num_CURs is depicted in Fig. 9. Its corresponding average response time is depicted in Fig. 10. In Fig. 9, we show that the performance of each scheme levels off or begins to be degraded beyond the num_CURs of 100 to 200. The results indicate that CT_PACK is capable of providing superior performance. This performance gain is mainly because CT_PACK used empty space packing for best space-efficiency, and this leads CT_PACK to reduce the number of write operations by shortening the depth of the index tree nodes. As compared to column search operations, column update operations are write-intensive in the sense that update operations should perform the slow writes and erase operations in flash memory. In this write-intensive situation, we observed that CT_EaP showed a remarkable performance difference compared to the BT_BAS. The performance gain of CT_PACK and CT_EaP relative to BT_BAS reaches 20.2% and 30.7%, respectively, throughout the whole range of num_CURs. This fact can be confirmed by the results in Fig. 10. Actually, the response time of CT_EaP is 21% lower than BT_BAS at the overall range of num_CURs. Moreover, CT_EaP requires small volume of flash memory writes for the column update operation, as compared to BT_BAS. We then analyzed the results of the experiments under the high workload condition, TestSet2. As mentioned above, TestSet2 used the mixed query, which consists of 75% of search operations and 25% of update operations. The throughput of mixed operations as a function of num_MORs and the number of mixed operation requests per second is presented in Fig. 11. Its corresponding average response time is depicted in Fig. 12. As the num_MORs increases, in Fig. 11, the overall throughputs of the four schemes in TestSet2, are gradually degraded as in TestSet1. This is mainly because more mixed operations TestSet2 induces more read contention and much higher compression delay, which is associated with update operations. Furthermore, in the respect of flash memory, update operations consume a much longer holding time than search operations, since write operations require additional overheads for erasing flash blocks. These data contentions and compression delays, in turn, lead to longer response times, as the num_MORs increases. This can be confirmed by the results in Fig. 12. That is, the average response time of all of the four schemes gradually increases in TestSet2. However, in the overall range, the response time curve of CT_EaP is much lower than that of BT_BAS. Note that this superior result is mainly because CT_EaP enhances update speed by packing empty space for space-efficiency and enhances search speed by embedded segment indexing under the heavy workload condition of TestSet2. With respect to the response time of a mixed operation, the gain of CT_PACK relative to BT_BAS reaches about 40.7% and that of CT_EaP reaches about 52.9%. In TestSet2, we observed that CT_EaP, followed by CT_PACK, CT_EMB, and BT_BAS, exhibits the highest throughput. With respect to the throughput of a mixed operation, the performance gain of CT_PACK relative to BT_BAS reaches about 22.3% and that of CT_EaP reaches about 29.1%.
There is a trade-off in employing an embedded segment index in the sense that this mechanism certainly requires a small overhead to maintain a segment offset in leaf nodes. However, it does save up to 30% of the unused space. In our scheme, the size of each segment offset is 4-bytes of an unsigned integer. The array size of the segment offsets is 10, which is a sufficient number to keep multiple segments. Thus, the space overhead for maintaining an embedded segment index is less than 40-bytes. In the case of first test set, the average I/O size of the column data updates is about 3.7 kbytes and thus, the space overhead is about 1.1%. In a heavy-workload case, the average size of column data updates is about 7.2 kbytes and thus, the space overhead is about 0.6% at most. Therefore, the CaF index scheme can save about 28.9% in flash memory.
Moreover, as shown in our results, the superior search performance of our scheme compensates for this overhead, especially in read-intensive high-performance databases. Additionally, the CaF index enhances the power consumption and the lifetime of the flash memory by reducing the volume of I/O data.
5. Conclusion
Column-oriented database systems are being increasingly adopted in the commercial marketplace due to their I/O efficiency on read-mostly applications such as data warehouses that serve customer relationship management and business intelligence applications.
We have proposed a CaF index management scheme based on flash memory in order to enhance index operation performance in column-oriented database systems. Unlike the previous B+-Tree index, the CaF index scheme improves search operation performance by using unused space packing in internal and leaf nodes. The CaF index scheme also exploits the embedded segment index to shorten the index traverse range of column data and to reduce the uncompression overhead in leaf nodes.
We used two types of databases from a game portal and a network company. The results obtained from our performance evaluation show that the CaF index management scheme outperforms the traditional B+-Tree index scheme in terms of mixed operation response time and mixed operation throughput, especially in the high workload condition.
Biography
Si-Woo Byun
He received a B.S. degree in Computer Science from Yonsei University in 1989 and earned his M.S. and Ph.D. in Computer Science from Korea Advanced Institute of Science and Technology (KAIST) in 1991 and 1999. Currently, he is teaching and researching in the area of distributed database systems, embedded systems, mobile computing, flash memory database, and fault-tolerant systems in Anyang University.
Biography
He received the B.S., M.S., and Ph.D. degrees in Computer Science from Soongsil University, Seoul, Korea, in 1995, 1997, and 2000, respectively. He is currently working as an Assistant Professor at Anyang University, Korea. His primary research interests include robot vision, fuzzy systems, augmented reality, video indexing and retrieval, intelligent game, biometrics and pattern recognition.
References
1. DJ. Abadi, PA. Boncz, and S. Harizopoulos, "Column-oriented database systems," Proceedings of the VLDB Endowment, vol. 2, no. 2, pp. 1664-1665, 2009.  2. R. MacNicol, and B. French, "Sybase IQ multiplex-designed for analytics," in Proceedings of the 30th International Conference on Very Large Data Bases (VLDB’04), Toronto, Canada, 2004, pp. 1227-1230.  3. M. Stonebraker, DJ. Abadi, A. Batkin, X. Chen, M. Cherniack, M. Ferreira, and et al, "C-store: a column-oriented DBMS," in Proceedings of the 31st International Conference on Very Large Data Bases (VLDB’05), Trondheim, Norway, 2005, pp. 553-564.
4. S. Byun, "Column-aware polarization scheme for high-speed database systems," Journal of Korean Society Internet Information, vol. 13, no. 3, pp. 83-91, 2012.  5. YH. Chang, JW. Hsieh, and TW. Kuo, "Endurance enhancement of flash-memory storage systems: an efficient static wear leveling design," in Proceedings of the 44th annual Design Automation Conference, San Diego, CA, 2007, pp. 212-217.  6. S. Byun, "Enhanced index management for accelerating hybrid storage systems," Journal of Convergence Information Technology, vol. 4, no. 2, pp. 164-169, 2009.  7. DJ. Abadi, SR. Madden, and N. Hachem, "Column-stores vs. row-stores:how different are they really?," in Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, Vancouver, Canada, 2008, pp. 967-980.
8. SK. Cha, JH. Park, and BD. Park, "Xmas: an extensible main-memory storage system," in Proceedings of the 6th International Conference on Information and Knowledge Management, Las Vegas, NV, 1997, pp. 356-362.  9. R. Elmasri, and S. Navathe, in Fundamentals of Database System, 6th ed, Upper Saddle River, NJ: Pearson Education, 2010.
10. CH. Wu, LP. Chang, and TW. Kuo, "An efficient R-tree implementation over flash-memory storage systems," in Proceedings of the 11th ACM International Symposium on Advances in Geographic Information Systems, New Orleans, LA, 2003, pp. 17-24.  11. H. Lu, YY. Ng, and Z. Tian, "T-tree or b-tree: main memory database index structure revisited," in Proceedings of the 11th Australasian Database Conference (ADC2000), Canberra, Australia, 2000, pp. 65-73.
12. C. Lee, K. Ahn, and B. Hong, "A study of performance decision factor for moving object database in main memory index," in Proceedings of the Korea Information Processing Society 2003 Spring Conference, Seoul, Korea, 2003, pp. 1575-1578.
14. D. Roberts, T. Kgil, and T. Mudge, "Integrating NAND flash devices onto servers," Communications of the ACM, vol. 52, no. 4, pp. 98-103, 2009.  17. Y. Li, B. He, RJ. Yang, Q. Luo, and K. Yi, "Tree indexing on solid state drives," Proceedings of the VLDB Endowment, vol. 3, no. 1–2, pp. 1195-1206, 2010.  18. CH. Wu, LP. Chang, and TW. Kuo, "An efficient B-tree layer for flash-memory storage systems," in Proceedings of 9th International Conference on Real-Time and Embedded Computing Systems and Applications (RTCSA2003), Tainan City, Taiwan, 2003, pp. 409-430. 
Fig. 1
Flash memory architecture. 
Fig. 2
Leaf node structure of column-aware flash memory-based index (CaF index). H=header of original index, h1=header of Embedded Segment1, d1=compressed data of Embedded Segment1. 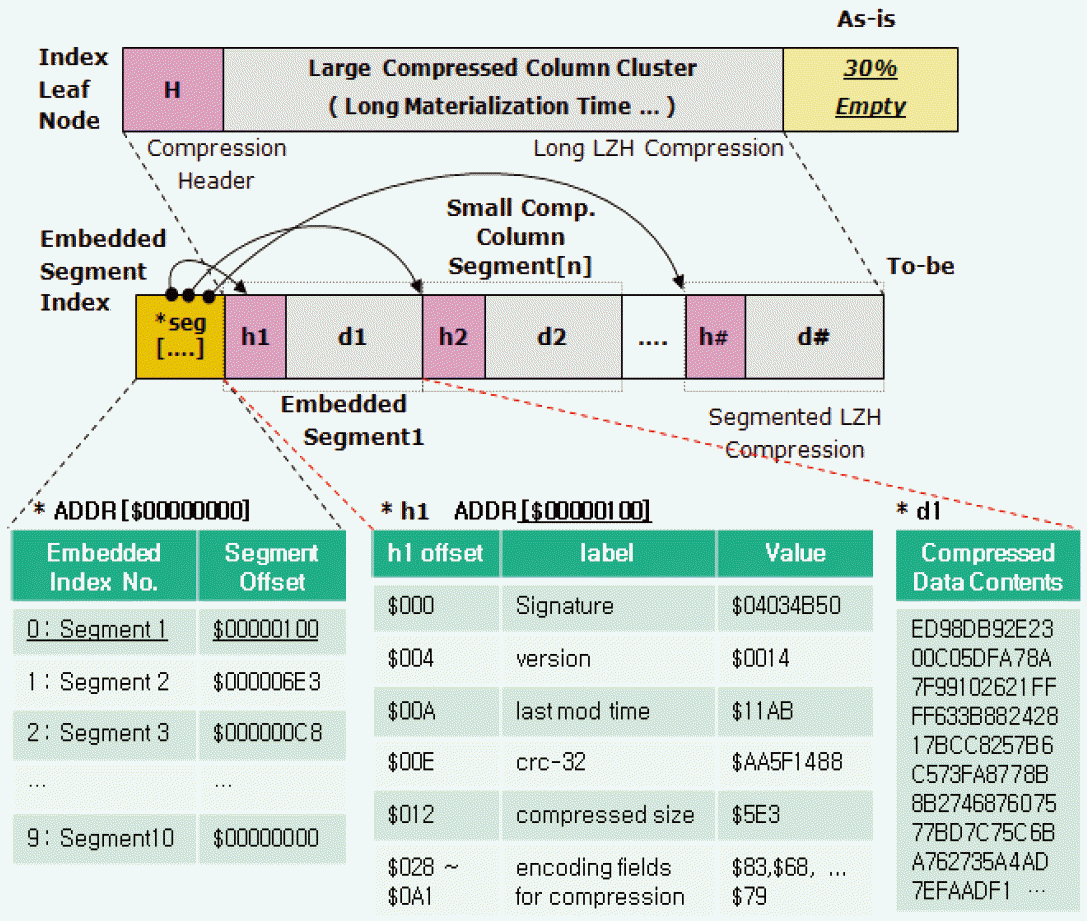
Fig. 3
Internal node structure of column-aware flash memory-based index (CaF index). X=search key in subtree, Ki=ith key, Pi=ith pointer. 
Fig. 4
The overview of the example FD-Tree. 
Fig. 5
Flow of search operation. 
Fig. 6
Search-operation throughput. 
Fig. 7
Search-operation response time. 
Fig. 8
Search-operation queue-length. 
Fig. 9
Update-operation throughput. 
Fig. 10
Update-operation response time. 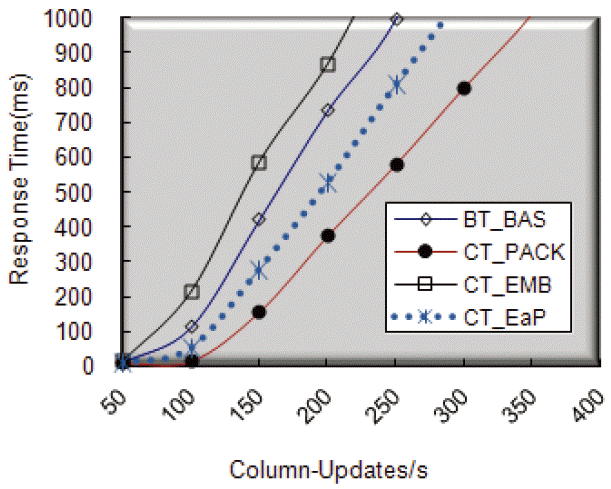
Fig. 11
Mixed-operation throughput. 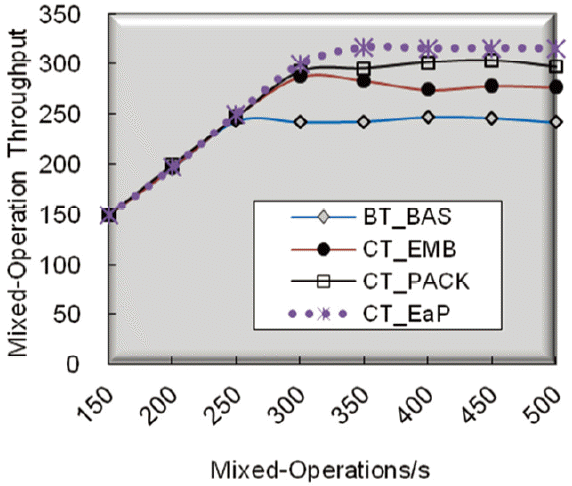
Fig. 12
Mixed-operation response time. 
Table 1
Column characteristics of game play database (TestSet1)
|
Column name |
ItemUseNo
|
UserNo
|
GameCode
|
GameCheat
|
UseDate...
|
|
Compression time for 10,000 records (ms) |
30 |
22 |
25 |
8 |
48 |
|
Column data size of 10,000 records (byte) |
2,379 |
659 |
1,905 |
192 |
13,597 |
|
Compression ratio |
4 |
1 |
2 |
0.3 |
8 |
|
Sample value 1 |
25 |
12 |
202956801 |
TRUE |
2012-2-16 17:16 |
|
Sample value 2 |
93 |
21 |
202956801 |
TRUE |
2011-2-19 19:43 |
Table 2
Column characteristics of network flow database (TestSet2)
|
Column name |
FST_FIN_TM
|
SVR_RTT_TM
|
CLI_RTT_TM
|
SESS_START_TM...
|
|
Compression time for 10,000 records (ms) |
40 |
36 |
30 |
82 |
|
Column data size of 10,000 records (byte) |
1,782 |
1,562 |
699 |
32,200 |
|
Compression ratio |
2 |
2 |
1 |
10 |
|
Sample value 1 |
183.168 |
16.182 |
0.072 |
2013-02-01
10:53:05.000000 |
|
Sample value 2 |
183.192 |
16.179 |
0.076 |
2013-02-02
17:15:43.000000 |
Algorithm 3.1
Search and Update Operation of CaF Index Scheme
|
ColumnData *CaF-Operation (int key, type operation, optional newdata) {
|
|
R ← node containing root of tree; |
|
N ← FM-Read(R); |
// read node R in Flash Memory |
|
while ( Type(N) != LEAF_NODE ) {
|
// N is not a leaf node of the tree. |
|
q ← number of tree pointers in node N
|
|
if ( key ≤ N.K1 )
|
// N.Ki refers to the ith search field value in node N.
|
|
N ←N.P1
|
// N.Pi refers to the ith tree pointer in node N.
|
|
// N is the first child node. |
|
else if ( key > N.Kq−1 )
|
|
N ←N.Pq
|
// N is the last child node. |
|
else {
|
|
Search node N for an entry i such that N.Ki−1 < key ≤ N.Ki ; |
|
N ←N.Pi
|
|
}
|
|
N ←FM-Read(N); |
// read internal node N
|
|
} // end of while loop |
|
Create a temp node T in RAM for fast uncompression;
|
|
S ← FM_Read( N + N.SegmentOffset[N.Ki] ) |
// jump uncompression pointer to Segment S.
|
|
T ← Lzo_Uncompress_Segment(S);
|
// uncompress only segment S
|
|
if (operation==SEARCH) { |
|
Search Data Di such that key = Ki in T; |
// search target data Di.
|
|
Return Di
|
// return data Di
|
|
} else if (operation==UPDATE) {
|
|
Search Data Di such that key = Ki in T; |
// search target data Di.
|
|
Update data Di to new data in T; |
|
S ← Lzo_Compress_Segment(T );
|
|
FM_Write(S );
|
|
} else if (operation==DELETE) {
|
|
Search Data Di such that key = Ki in T; |
// search target data Di.
|
|
Remove data Di and its pointer in T; |
|
S ← Lzo_Compress_Segment(T );
|
|
FM_Write(S );
|
|
Merge if the number of leaf nodes is less than the minimum; rebalance internal nodes;
|
|
} else if (operation==INSERT) {
|
|
Find data location such that key = Ki in T; |
|
insert data in the location of T; |
|
S ← Lzo_Compress_Segment(T );
|
|
FM_Write(S );
|
|
Split if the leaf node is full; rebalance internal nodes; |
|
}
|
|
Return OP_SUCCESS;
|
|
} // End of CaF-Index Operation |
|













