Genetic Symmetric Key Generation for IDEA
Article information
Abstract
Cryptography aims at transmitting secure data over an unsecure network in coded version so that only the intended recipient can analyze it. Communication through messages, emails, or various other modes requires high security so as to maintain the confidentiality of the content. This paper deals with IDEA’s shortcoming of generating weak keys. If these keys are used for encryption and decryption may result in the easy prediction of ciphertext corresponding to the plaintext. For applying genetic approach, which is well-known optimization technique, to the weak keys, we obtained a definite solution to convert the weaker keys to stronger ones. The chances of generating a weak key in IDEA are very rare, but if it is produced, it could lead to a huge risk of attacks being made on the key, as well as on the information. Hence, measures have been taken to safeguard the key and to ensure the privacy of information.
1. Introduction
With the advent of the computer era, data security has become an urgent neccesity. To achieve this, various data threats must be mitigated to maintain the authenticity, confidentiality, and integrity of data.
There are two cryptographic techniques—symmetric key cryptography and asymmetric key cryptography [1]—both of which are implemented by various algorithms that are defined in this field. In this research paper, we consider International Data Encryption Algorithm (IDEA), which is a symmetric key algorithm, for the purpose of encryption and decryption.
A genetic algorithm (GA) is a search heuristic that is used to portray the process of natural evolution. This algorithm provides solutions to optimization and search problems [2].
The proposed method in this paper uses a GA for the generation of a 128-bit symmetric key that is used in IDEA. It inhibits the creation of any weak key for this cryptographic technique.
The remainder of this paper is laid out as follows: Section 2 describes the basics of IDEA and also sheds some light on the fundamentals of the GA and its operators. Section 2.1 explains some of the related work done so far on this issue. Section 3 includes the methodology that we adopted to generate a symmetric key genetically. In Section 4, the results from using this methodology are illustrated. Section 5 concludes the paper and briefly mentions the areas that should be examined for future research.
2. Related Work
The concepts used in this paper include the block cipher IDEA and the basics of a GA. IDEA works on 64-bits of plaintext and a 128-bit symmetric key and involves 8 rounds. The algebraic operations used in IDEA include XOR (bitwise addition modulo 2), Addition modulo 216 and multiplication modulo (216 + 1). The key generation cycle differs for encryption and decryption in IDEA. It requires 52 keys that are 16-bits each, where 4 keys are used for last round of output transform and 6 keys in each of the previous 8 rounds [1].
GAs are based on the concept of ‘survival of the fittest’ and work to find the optimal or near optimal solution for the optimization problems. The idea behind GA is to model the natural selection process where some individuals are selected from the population and where genetic operators are applied to produce improved generation. The genetic operators involved are:
Selection Operator: the motive behind this operator is to select the best parents, so as to transfer better characteristics to next generation. The goodness of each individual in a particular generation depends upon its fitness, which may be calculated by an objective function or by a subjective judgment [3].
-
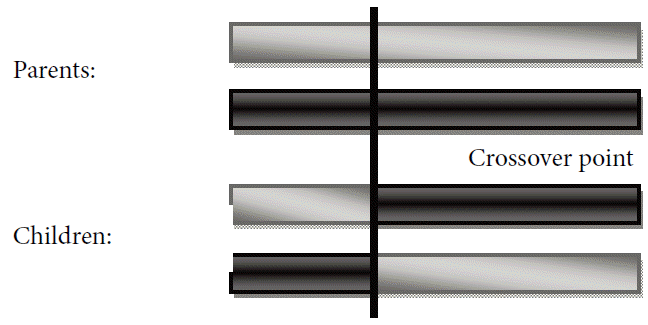
Crossover: the two best individuals are chosen using the selection operator and a crossover site is randomly chosen. Bits are exchanged in the bit strings up to the crossover point.
For example:
If S1 = 11111111 and S2 = 00000000 and the crossover point is 5, then S1′=11111000 and S2′= 00000111.
Crossover is likely to produce better offspring, as compared to the parent bit strings. Crossover can be categorized as: One point or Single, Two point or Double, Uniform, Half-Uniform, Cut and Splice.
Single crossover includes the swapping of bits across a randomly selected crossover bit as shown in Fig. 1 below.
Double crossover includes the selection of two random bits and swapping the bit strings across them, as represented in Fig. 2.
There are a few other crossover techniques that are based on swapping of bits, but these are not discussed in detail in this paper [3].
-
Mutation: some of the bits of the parent bit strings will be flipped or toggled in order to maintain diversity within the population, as illustrated in Fig. 3 below.
The figure above mutates the bit string around bit 4.
There are numerous explorations that have been carried out so far with regards to IDEA and the Genetic Algorithm. Research has been executed in the field of the cryptanalysis of various rounds of IDEA. In 1993, Hawkes extended the study of Daemen et al. [5], which identified certain weak classes for IDEA. In 1998, Hawkes [5] presented a related key differential attack on 4 rounds of IDEA. Moreover, he identified large weak key classes for 4.5–6.5 rounds and 8 rounds of the algorithm [5]. Biryukov et al. [6] identified a few classes of weak keys in 2002. In 2010, Zhu [7] further put forward an attack on 5.5 rounds of IDEA. Also, in 2010, Abed [7] proved that the GA gives optimal keys and enhances the security of the key. He used the RC4 algorithm and applied it to images [8]. In 2011, Bhowmik and Acharyya [9] worked on images and combined GA with Blowfish. In 2012, Goyat [9] proved that the GA maintains the strength of the asymmetric key. She presented the idea that random numbers that are generated should be secure enough against attacks [10]. Most of the research that has been done on IDEA, as well as using the genetic approach, involves conducting cryptanalysis on various rounds of IDEA and on various ciphers, respectively. This research paper provides an optimal solution for the problem of weak keys.
3. Proposed Algorithm
This section is about the new approach that we devised to overcome the shortcomings of IDEA in regards to the generation of weaker keys.
3.1 Proposed Methodology
The weakness of the IDEA led to the generation of a symmetric key that could be used for encryption and decryption genetically. These keys are detectable in a chosen plaintext attack. It helps in easy anticipation of relationship between the XOR sum of the plaintext and the ciphertext.
For example:
All zeros (0x0000000000000000)
All ones (0xFFFFFFFFFFFFFFFF)
Alternating ones + zeros (0x0101010101010101)
Our algorithm is based on four classes of weak keys that have been identified [4].
-
The first category of weak keys includes the keys that are responsible for a linear factor (i.e., a linear relation between certain input and output bits that have a definite probability). The keys are of the form:
0000 00ab 0000 000000c0 0000 000d xyzt
where,
a = 0, 1, 2, 3
b = 0, 8
c = 0, 2, 4, 6, 8, 10, 12, 14
d = 0, 1
x, y, z, t = any value
(223 keys)
-
The second category of weak keys includes the keys for which a change in certain bits of input makes the change in output bits identifiable with a definite probability. The keys are of the form:
0000 00ax yzb0 0000 00tc 0000 000u vwd0
where,
a = 0, 1, 2, 3
b = 0, 8
c = 0, 8
d = 0, 2, 4, 6, 8, 10, 12, 14
x, y, z, t, u, v, w = any value
(235 keys)
-
The third category of weak keys includes the keys that are predictable if certain ciphertext bits are known to correspond to the plaintext. The keys that belong to this category are of the form:
0000 00ax yzb0 0000 00tu v000 cwsq prd0
where,
a = 0, 1, 2, 3
b = 0, 8
c = 0, 1
d = 0, 2, 4, 6, 8, 10, 12, 14
x, y, z, t, u, v, w, s, q, p, r = any value
(251 keys)
-
Another category of weak keys for IDEA are identified as:
0000 0000 0x00 00000000 000x xxxx x000
where ‘x’ can be any hexadecimal number.
These key forms make the bitwise XOR of ciphertext bits predictable from the bitwise XOR of plaintext bits. The detected weak key cannot be used for the purpose of encoding and decoding the information. Hence, it requires further processing. The proposed algorithm solves the defined problem by applying the GA to the weak key. This results in a stronger key that can be used for the purpose of encipherment and decipherment being returned.
3.2 Genetic Key Generation – The Proposed Algorithm
To overcome the problem of weak keys in IDEA, we treated a weak key with the GA to convert it into a stronger one.
Diagrammatically, the proposed algorithm can be represented as shown in Fig. 4.
The algorithm can be explained by the following steps:
Step 1: Generate the initial population of a definite population size (POP_SIZE) randomly. Each key generated is 128-bits in length.
Step 2: Select one random key (K) from the generated population of the specific POP_SIZE.
Step 3: To check whether the key (K) is a strong or a weak key, perform a fitness check based on the categories of weak keys that were produced earlier. Each weak key category has a predefined format. If the key is found to be weak, go to Step 4. Otherwise go to Step 8.
Step 4: Divide ‘K’ into two sub-keys (K1 and K2) that are 64-bits each. These represent the two parents who will participate in the genetic process to produce improved offspring.
Step 5: Randomly generate the crossover bit from 0–63 and perform the crossover between K1 and K2 to produce two child bit strings (C1 and C2).
Step 6: After crossover, concatenate the two offspring (C1 and C2) to generate a 128-bit key (K′). If the newly generated key (K′) is same as that of the input key (K) with the crossover operation, perform the operation again.
Step 7: Once a new key is produced, perform a mutation operation. Randomly generate ‘N’ numbers from 0–127 and toggle the bits present at those N bit locations. Assign this new key to K. Go to Step 3 and perform a fitness check again.
Step 8: Use the strong key that was generated as a symmetric key in IDEA.
The strong key returned by the algorithm is further used for the purpose of encipherment in IDEA. The IDEA encryption process is performed as described in the steps for a standard algorithm [1]. IDEA, which is a symmetric key cipher, uses the same strong key for the purpose of decipherment as well.
4. Results and Discussions
We implemented the algorithm using Java Standard Edition ver. 4 update 21, (i.e. build 1.7.0_ 21- b11). The Integrated Development Environment (IDE) used to develop the code was NetBeans IDE 7.0.1. Apart from the technical details it is worth mentioning that NetBeans is a widely used framework that is fully equipped to work with Java. Java is an object-oriented language that follows the WORA (Write Once Run Anywhere) concept. Thus, code developed on one platform can be executed on any other platform too. Hence, Java is a good option for developing the code on.
4.1 Illustration
This section illustrates the results obtained by the implementation of the algorithm. In the first step of the algorithm, the initial population of a defined size (POP_SIZE) is generated. The POP_SIZE considered in this implementation is 20. Thus, 20 keys that are 128-bits each are produced. Moreover, all the keys produced are weak and belong to one category or another, as defined in Section 3.1. The weak keys that are generated are as follows:
{00000028000000000040000000006e9e,000000280000000000c0000000007099,000000280000000000
60000000002994,00000000000000000060000000009ad0,00000020000000000040000000005d34, 0000
001db080000000580000000ac0e0, 000000265a00000000980000000660e0, 0000003c44800000006800
0000018de0,0000002033800000004000000009ec20,0000002a0b00000000d80000000c12a0,00000010ec
8000000070a0001c32ad60,00000025d1000000008af0000b561960,0000000dff000000000bd00004eb942
0,000000344a000000009d500012e89460,00000006008000000070e0001e754260,000000000500000000
0000052f230000,00000000090000000000000bb218f000,00000000060000000000000b31b7d000,00000
00003000000000000044e002000, 0000000005000000000000075006a000}
From the 20 weak keys generated, one of the keys is randomly selected. In this illustration, a randomly selected key is:
0000000dff000000000bd00004eb9420
The binary equivalent of the Hex key is:
000000000000000000000000000011011111111100000000000000000000000000000000000010111101 00000000000000000100111010111001010000100000
This key belongs to the weak key Category 3, as defined earlier.
As a weak key cannot be used for the purpose of encryption in IDEA, we applied GA, so as to convert the selected weak key into a stronger one. Dividing the 128-bit key into two sub-keys of 64-bit each produces the two parent keys of:
Parent 1: 0000000000000000000000000000110111111111000000000000000000000000 Parent 2: 0000000000001011110100000000000000000100111010111001010000100000
Next, apply the crossover operator to the sub-keys. In our case, the crossover bit that was randomly selected from 0–63 is 29. The bits were then swapped over this bit, which resulted in two child bit strings:
Child 1: 0000000000000000000000000000110000000100111010111001010000100000 Child 2: 0000000000001011110100000000000111111111000000000000000000000000
The concatenated 128-bit key after crossover is:
000000000000000000000000000011000000010011101011100101000010000000000000000010111101 00000000000111111111000000000000000000000000
Next, randomly generate 10 mutation bits and toggle those bits. The key after mutation is:
000000000001000001000000001011000000010011101011100101000010011000000100000010111101 10010000000011111111000000000000000001000000
The hex equivalent of this key is:
0010402c04eb9426040bd900ff000040
A fitness check is then performed again for this final key, which declares this as a strong key.
4.2 Performance Analysis
In comparing the two keys, one in the original form and the second, which is generated by applying GA to the original, we observed that the original key has more bits that are ‘0’ than the newly generated, genetically stronger key. This is illustrated as shown below.
Old weak key: 0000000dff000000000bd00004eb9420 New strong key: 0010402c04eb9426040bd900ff000040
This strong key is the final key that is given to IDEA for encryption. The same key is stored in a file so that it can then be used for the decryption process. Evidently, any weak key that would have been generated can be treated with GA. Thus, we concluded that GA can solve the problem of weak keys in IDEA.
Moreover, the CPU time that corresponds to the file size is as shown below. Fig. 5 clearly represents that CPU Time is directly proportional to the file size. Also, it takes more time to encrypt than to decrypt, as GA is applied only during key generation before encryption. For decryption, the key is directly recovered from the file where it is stored.
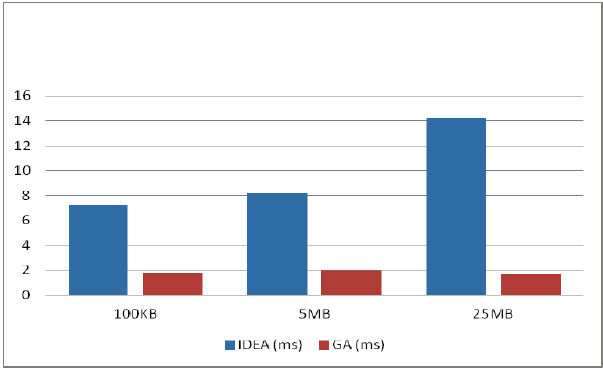
The second graph in Fig. 6 depicts that the CPU Time taken by IDEA is much more than the time taken by GA. Thus, we concluded that applying GA does not result in noticeable overhead. Moreover, we observed that the CPU Time taken by GA is independent of the file size. It is almost constant. Hence, it is an optimal solution for the considered problem.
5. Conclusion
To conclude, this paper is an effort to introduce a genetic approach in the symmetric key generation of IDEA, so as to solve the problem of weak keys. The performance of the proposed algorithm makes the approach worth adopting, as it covers the risk of producing any type of weak keys. The best feature of this algorithm is that it can be applied to any type of information be text, images, or multimedia (audio or video).
In short, our approach mitigates the occurrence of any possible weak keys in IDEA. Hence, it mitigates the possible attacks on ciphertext that has been encrypted using IDEA.
The work in this paper has a wide scope and can be extended in the field of cryptography. It is being applied to information that is encoded and decoded using IDEA. It can also be extended to the symmetric key generation of all of the algorithms that involve the risk of producing weak keys. Moreover, it can be extended in reference to the genetic operators of crossover and mutation. In this paper, one-point crossover has been used, which may be replaced by any other category of a crossover operator. Similarly, mutation may be applied on a fixed or variable number of bits. Moreover, block size can be varied from two 64-bit blocks to four 32-bit blocks using the divide and conquer approach. It can be extended to asymmetric keys as well. Furthermore, the number of iterations can be increased to achieve improved results.
References
Biography
Nandini Malhotra http://orcid.org/0000-0002-1006-4337
She received the Master’s degree in Computer Science and Engineering from National Institute of Technology, Jalandhar in 2013. She completed her bachelor’s degree in Computer Science and Engineering from Punjabi University, Patiala. Her research interests include Cryptography, Network Security and Object Oriented Programming.

Geeta Nagpal
She received the Ph.D. degree in Computer Science and Engineering from National Institute of Technology, Jalandhar, India in 2013. She completed her Master’s degree in Computer Science from Punjab Agricultural University, Ludhiana. She is presently working as Associate Professor in the Department of Computer Science and Engineering at National Institute of Technology, Jalandhar. Her research interests are Software Engineering, Databases and Data Mining.