Classification of Textured Images Based on Discrete Wavelet Transform and Information Fusion
Article information
Abstract
This paper aims to present a supervised classification algorithm based on data fusion for the segmentation of the textured images. The feature extraction method we used is based on discrete wavelet transform (DWT). In the segmentation stage, the estimated feature vector of each pixel is sent to the support vector machine (SVM) classifier for initial labeling. To obtain a more accurate segmentation result, two strategies based on information fusion were used. We first integrated decision-level fusion strategies by combining decisions made by the SVM classifier within a sliding window. In the second strategy, the fuzzy set theory and rules based on probability theory were used to combine the scores obtained by SVM over a sliding window. Finally, the performance of the proposed segmentation algorithm was demonstrated on a variety of synthetic and real images and showed that the proposed data fusion method improved the classification accuracy compared to applying a SVM classifier. The results revealed that the overall accuracies of SVM classification of textured images is 88%, while our fusion methodology obtained an accuracy of up to 96%, depending on the size of the data base.
1. Introduction
Texture is one of the main characteristics of images as it contains important information about the structural arrangement of surfaces and their relationship to the surrounding environment. This can be seen in many images from multispectral remote sensed data to microscopic photography. Despite the lack of complete and formal definition of texture, a large number of approaches for texture segmentation/classification have been treated in the literature. In addition, texture-based segmentation has shown its importance in various applications ranging from computer vision, image synthesis, and biomedical image processing [1] to remote sensing [2]. Image segmentation is a fundamental problem in image processing, which is a prerequisite to high-level computer vision applications. It aims to divide an image representing a real scene or a synthetic one into classes or categories in correspondence to different objects and the background in the image. In the end, each pixel should belong to one class and only one. In other words, we look for the image to be partitioned into distinct segments, and each of them shares some features in common such as intensities, color, or texture. Particularly, image texture defined by repeated patterns of intensities adds a lot of complications in image processing tasks. A textured image often has several regions with different textures in existence, and the task of segmentation is to locate the texture boundaries. This is because the pixel near the texture boundary has neighboring pixels belonging to different textures. Many studies have been performed for the segmentation of the textured images, such as watershed transform [3], Markov random field [4, 5], probabilistic techniques [6], and wavelet transform [7].
The texture classification process usually involves two phases: the learning phase and the recognition phase. In the learning phase, the target is to build a model for the texture content of each texture class present in the training data, which is generally comprised of images with known class labels.
The texture content of the training images is captured with the chosen texture analysis method, which yields a set of textural features for each image. These features, which can be scalar numbers or discrete histograms or empirical distributions, characterize the given textural properties of the images, such as spatial structure, contrast, roughness, orientation, etc. In the recognition phase, the texture content of the unknown sample is first described with the same texture analysis method. Then, the textural features of the sample are compared to those of the training images with a classification algorithm, and the sample is assigned to the category with the best match.
A wide variety of techniques for modeling the texture have been proposed. The most popular feature extraction techniques are Gabor filters [8], co-occurrence matrix [9] and wavelets [10–13]. A comparative study has been presented by [14].
Wavelets have been identified as popular and effective texture characterization methods. Also, they have proved to give better texture characterizing results, even if their major problem is their lack of directionality and shift in variance. A complex wavelet decomposition was proposed to give directionally specific and shift invariant sub-bands, but our purpose is to fill this gap and to try to improve the performance of this system, therefore discrete wavelet transform (DWT) has been chosen in this paper as a key method for texture characterization.
Texture segmentation can be pixel wise or block wise. Pixel wise segmentation schemes evaluate the texture features in a neighborhood surrounding each pixel in the image. The advantage of pixel wise segmentation over block wise lies in the removal of blockiness. For this reason, we chose pixel wise segmentation to extract features.
After a proper texture feature extraction by wavelet transform, a suitable classification algorithm is used. From among the most popular classifiers, we chose the support vector machine (SVM). It was initiated by [15] and is primarily a linear classification approach to two classes. It tries to separate individuals from two classes (+1 and −1) seeking the optimal hyper plane that separates the two sets. This guarantees a large margin between the two classes. In our case, SVM was used for a multiclass problem.
Several classifiers can give different answers about the assignment of a pixel of the image to a given class. This is due to the quality of the content of the pixel and the specific uncertainty of the classifier. This uncertainty depends on the model decision of the classifier and the database used for learning. As such, there is no classification method that can fully satisfy the requirements of a particular application. On the one hand, the combination of multiple classifiers decisions has been introduced by several authors to improve classification performance [16–18]. However, on the other hand, other authors combined different extraction feature techniques [19], and some works like [7,20] combined features provided by the same feature extraction technique. The author in [21] combined the classification results of sliding windows, using all the windows containing the area to conduct classification for sonar images. All of these techniques introduce the concept of data fusion.
Data fusion has been introduced to manage large amounts of multiple data sources in the military field. Recently, it was adapted to applications of signal processing. Bloch [22] defined data fusion as combination of information from multiple sources to help with decision-making.
Four levels of fusion have been introduced in [23], which are as follows: sensor level, feature level, score level and decision level.
In our work, we focused on the two fusions levels of score and decision level fusion. The first one is achieved by combining matching scores provided by the SVM classifier. The second one is used by combining decisions made by the same classifier. Three fusion methods were investigated and compared: majority vote rule, the rules based on the probability theory (product, min, and sum), and the fuzzy set theory. All of these process were carried out on the same image (one source) provided by the same classifier. Fig. 1 illustrate the two process carried out to improve classification accuracy.
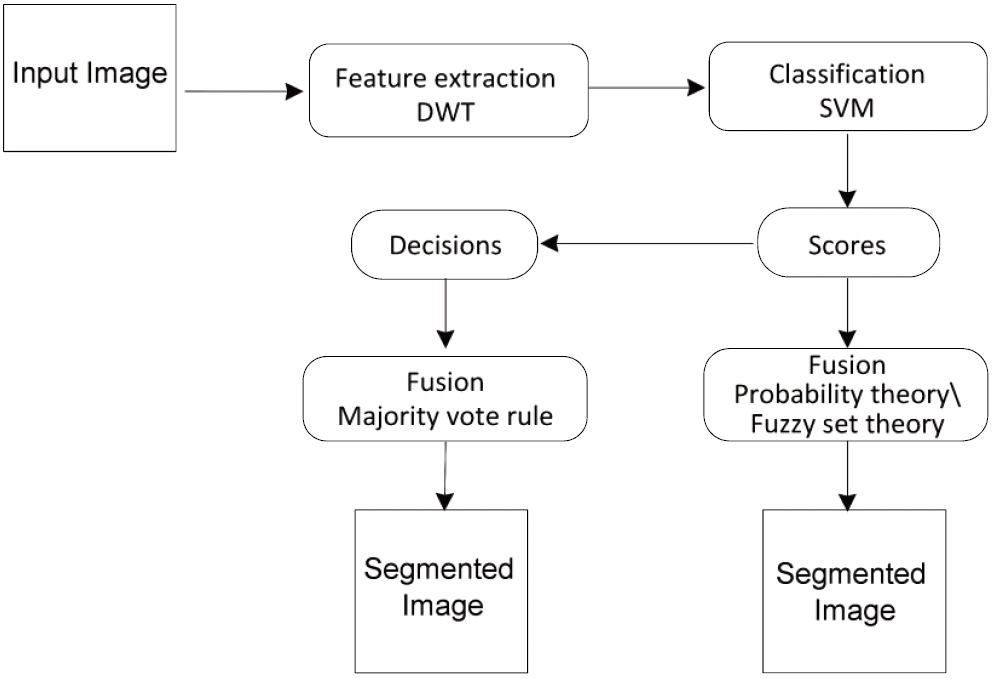
Textured image segmentation process based on scores and decisions fusion. DWT=discrete wavelet transform, SVM=support vector machine.
Experiments show that both decisions and score fusion level enhance classification accuracy. The remainder of this paper is organized as follows: Section 2 presents the background theory. The different steps followed in the proposed segmentation process are described in Section 3. Section 4 is dedicated to evaluating and comparing the performance of the described method. Finally, in Section 5, we conclude and suggest avenues for future work.
2. Background Theory
2.1 Texture Analysis
Texture analysis is a major step in texture classification, image segmentation, and image shape identification tasks. Texture analysis groups a set of techniques for quantifying the gray levels present in an image in terms of intensity and distribution in order to calculate the number of characteristic parameters of the considered texture.
It plays an important role in many image-processing tasks, ranging from remote sensing to medical imaging and industrial automation. Texture analysis is usually dealt with in two major phases. The first phase is feature extraction, in which the image information is reduced to a small set of descriptive features. The second step deals with classifying the features obtained from individual pixels (e.g., texture segmentation) or a collection of pixels (e.g., image classification).
2.1.1 Feature extraction
Instead of using the raw data, selected measurements (called “features”) extracted from the raw data are used as the basis for classification. Features should be designed to be invariant or less sensitive with respect to commonly encountered variations and distortions, whilst containing less redundancy. The extraction of a set of features produces a feature vector x that take the form: x = [x1, x2, x3 ..., xn] or by its transpose. The key decision is determining which features to extract. Various methods for texture feature extraction have been proposed over the last decades by [9–12, 14].
Because texture has so many different dimensions, there is not one single method of texture representation that is adequate for a variety of textures. We chose DWT in this paper as a key method for texture characterization because it has been identified as a popular and effective texture characterization method, even if it’s major problem is its lack of directionality and shift invariance. Our purpose is to fill this gap and try to improve the performance of this system.
Discrete Wavelet Transforms: Wavelets are functions that satisfy a linear combination of different scaling and translation of wave functions. Similar to the sinusoidal function in the Fourier transform, a wavelet is used as a basis function in representing a target function, a signal, or an image, as a superposition of wavelets. The main advantage of wavelets over other frequency methods, like Fourier transform, is that it provides both frequency and spatial locality.
Mallat [12] demonstrated that wavelet decomposition should be implemented by using two channel filter banks. One channel is a low pass filter (denoted as L), while the other channel is a high pass filter (denoted as H). Using these filters at each level of decomposition while down sampling the signal, enables simple decomposition by successive transforms.
On a two-dimensional signal, like an image, rows and columns are filtered separately. As a result of one decomposition level, we have four sub-bands or sub-images [10, 12] denoted as: LL, HL, LH, and HH. The wavelet coefficients obtained contain local frequency information at multiple levels of resolution. They are then manipulated to form a vector of textural characteristics.
2.1.2 Pixel classification
Classification refers to assigning a physical object or incident to one set of predefined categories. In texture classification, the goal is to assign an unknown sample image to one set of known texture classes.
The texture classification process involves two phases: the learning phase and the recognition phase. In the learning phase, the target is to build a model for the texture content of each texture class present in the training data, which is generally comprised of images with known class labels. The texture content of the training images are captured with the chosen texture analysis method, which yields a set of textural features for each image. These features, which can be scalar numbers or discrete histograms or empirical distributions, characterize the given textural properties of the images, such as spatial structure, contrast, roughness, orientation, etc. In the recognition phase, the texture content of the unknown sample is first described with the same texture analysis method. Then, the textural features of the sample are compared to those of the training images with a classification algorithm, and the sample is assigned to the category with the best match. In supervised classification, the spectral features of some areas of known land over types are extracted from the image. These areas are known as the “training areas.” Every pixel in the whole image is then classified as belonging to one of the classes depending on how close its spectral features are to the spectral features of the training areas, which is what we are focusing on in this paper.
In the case of supervised classification, a k-nearest neighbor (K-NN) and SVM [24, 25] classifiers are usually applied. In our work we applied a SVM classifier.
2.2 Information Fusion
The fusion of information consists of combining information originating from several sources in order to improve decision-making. Usually, information fusion [22] can be carried out at the four levels described below.
Sensor level fusion refers to the combination of raw data from different sensors.
Feature level fusion refers to the combination of different features vectors.
Score level fusion refers to the combination of matching scores provided by different classifiers.
Decision level fusion refers to the combination of decisions provided by individual classifiers.
Generally, a single classifier is unable to handle the wide variability and scalability of the data in any problem domain. Most modern techniques of pattern classification use a combination of classifiers [16] and fuse the decisions provided to improve the classification efficiency.
In our work, we focus on two fusion levels of score and decision level fusion. The first one is achieved by combining matching scores provided by the SVM classifier and the second one is used by combining decisions made by the same classifier. We investigated the three following fusion methods: majority vote rule, rules based on probability approach, and fuzzy set theory. All of these processes are carried out on the same image (one source) to take advantage of the redundancy of the same classifier.
2.2.1 Majority vote rule
The majority vote rule is the simplest approach for fusion due to its simplicity of implementation [22]. The class z most voted by the individual classifier is selected by computing the number of times that each class appears:
The coefficient αj represents the reliability degree of the classifier and we can estimate it by using the recognition rate of each classifier. These coefficients are used to tackle the problem of the conflict between classifiers. In our case, we omitted this coefficient because we used one classifier.
2.2.2 Fuzzy set theory
The fuzzy set theory [26] is an extension of the classical theory. The main advantage of this theory is the possibility to represent imprecision and uncertainty. The interest of fuzzy logic is to assign several classes to an observation with different membership degrees, and to postpone the final decision step. We are proposing the use of the fuzzy set theory for the SVM’s score fusion to improve classification performance.
Let A = {x1, ..., xc} be a fuzzy set in the universe of discourse U (in our case, the set of class labels), defined as A = {μA(xi), xi}i = 1, 2... c where, the membership function μA(xi) having positive values in the interval [0 1] denotes the degree to which an event xi may be a member of A.
Estimating the membership function is a difficult step in fuzzy logic theory. Several modes of intra-class combination (because it refers to the fusion of observations from the same class), have been proposed in [27]. There are three combination families, which are as follows: conjunctive combination, disjunctive combination, and compromise combination.
The decision is the final step. It is made once all of the membership degrees have been combined into a single one. Generally, we took into account the maximum of one of these: membership degree, expectancy, likelihood, or entropy. We chose the criterion that employs the maximum membership degree, which provides better results.
3. The Proposed Segmentation Algorithm
The classification of pixels is based on the use of supervised classification approaches and on texture features. Using a sliding window (a block of 15×15 pixels) with a recovery step, the class for this window is assigned to its central pixel. However, this central pixel belongs to other window neighbors that can be classified into other classes. For this reason, we are proposing a fusion of the classification results of different windows that contain this central pixel.
3.1 Pixels Classification
The system applies a wavelet transform of level 1 Haar wavelet to the entire textured image (cf. Fig. 2), and it extracts features from each image detail (dl, l=1…4) denoted as: LL1, HL1, LH1, HH1, where 1 is designated as the first level.
Application of 1-level discrete wavelet transform (DWT).
LL1 contains both horizontal and vertical low frequencies: approximation coefficients.
LH1 contains horizontal low frequencies and vertical high frequencies: vertical details.
HL1 contains horizontal high frequencies and vertical low frequencies: horizontal details.
HH1 contains both horizontal and vertical high frequencies: diagonal details.
Pixel wise segmentation has been chosen rather than block wise [10]. Different tests have been carried out on a range of window sizes from 7×7 to 23×23. The results of the experiments show that the block size of 15×15 is the proper one for texture discrimination.
We computed the mean and standard deviation over the sliding window W from the corresponding channel as:
where, Nw denotes the number of pixel in the window W.
Finally, the feature vector corresponding to each pixel is composed of eight parameters. Illustration of the feature extraction process is presented in Fig. 3.
Texture features extraction using discrete wavelet transform (DWT).
For the training data we extracted features from samples of the remaining classes the same way as we did for the testing data. The estimated feature vector of each pixel is sent to the SVM classifier for an initial labeling.
3.2 Fusion for Post-Classification
Let I be the segmented image containing the class decisions of each pixel (the output of the SVM classifier) I = dij with i = 1 ... n and j = 1 ... n. We browsed the image by using a sliding window of size N × N, so that each pixel is surrounded by N2 – 1 pixels.
Each central pixel pij,l of window wl with decision dij,l belongs to the N2 – 1 window in a different position before the classification process. Whereas, each central pixel pij,m of the windows m with m = 1... N2 — 1 made different decisions dij,m.
For example, in the case of pixel p3,3 with decision d3,3 and N = 3, the central pixel is surrounded by eight pixels, which are the center of the eight windows that pixel p3,3 belonged to.
The same process is applied for the matrix scores provided by the SVM classifier instead of the decision matrix.
3.2.1 Decision fusion
Using the example above, we combined the decisions made by the actual block and its eight surrounding ones of {d3,3, d3,2, d3,4, d2,3, d2,4, d2,2, d4,2, d4,4, d4,3} by applying majority vote rule (cf. Fig. 4).
Decisions fusion process.
The objective is to take into account the multiple decisions of the different blocks when the central pixel appears to improve decision-making.
3.2.2 Scores fusion
Let S be a matrix containing the scores of each pixel to each class provided by SVM, S = slk with l = 1 ... M and k = 1 ... C where, M = n × mis is a number of pixels of the image and C is the number of classes. We decomposed the S to k image, which was used as the source of information for data fusion
Scores fusion process.
Rules based on the probability theory
This approach consists of combining the scores offered by the SVM classifier, which are the posterior probabilities
Rules based on the fuzzy set theory
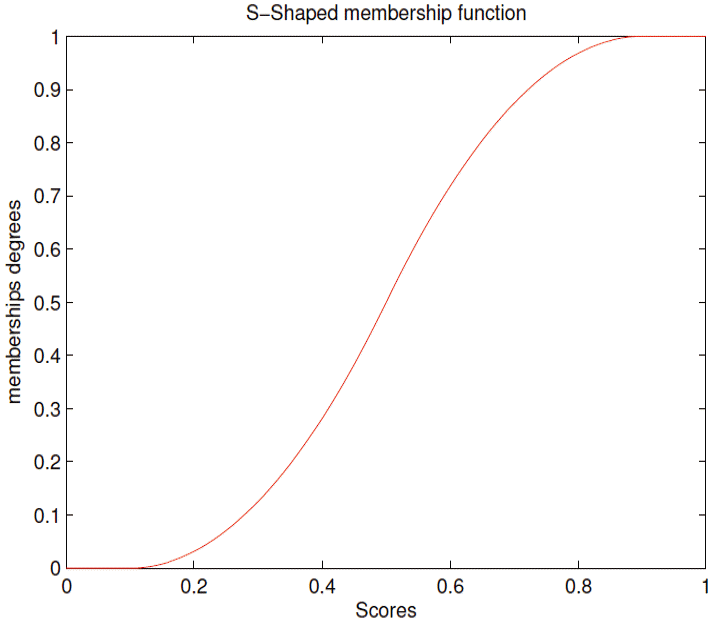
This approach consists of transforming the probability provided by the SVM classifier to membership degrees via the S-shaped membership function (cf. Fig. 6).
S-shaped membership function.
The advantage of the fuzzy set theory over the modeling of the imprecision of information is the large variety of combination operators. We investigated several ways to implement the combination of these membership degrees as follows:
With
4. Experiments Results
4.1 Pixels Classification
We demonstrated the procedure and performance of the proposed algorithm by segmenting a textured image. Fig. 7(a) illustrates a textured image containing four natural textures from the Brodatz album (http://multibandtexture.recherche.usherbrooke.ca/original_brodatz_more.html) of D16, D77, D21, and D32.
(a) Textured image (256×256) obtained from the Brodatz album. (b–d) Segmented image by support vector machine (SVM) classifier for 400, 4000, 8000 samples, respectively.
Fig. 7(a) has been decomposed by DWT on the first level with a Haar wavelet. The features were extracted from the multichannel images by using a sliding window W (15×15) over each channel. For the training data, we extracted a number of samples with the same size of W for each class. Fig. 7(b)–(d) shows the segmented results by SVM classifier by selecting 400, 4,000, and 8,000 samples, respectively, from each class.
For each experiment, we used the percentage of correct classification to evaluate the classification accuracy.
Table 1 shows the recognition rates that were obtained by using different sizes of the training database with the DWT and SVM classifier. The best result was obtained using 8000 samples with recognition rates of 92.66%.
Recognition rates according to training data base size
As seen in Fig. 7, the four textures are not well discriminated. So, in order to improve classification accuracy we integrated a fusion scheme in the decision and score level.
4.2 Fusion Scheme
The first fusion scheme consists of combining the decisions made by SVM classifier, as mentioned in Fig. 4 and the result is shown in Fig. 8. The window’s size of 15×15 is the proper one for both decision and score level fusions.
(a–c) Segmented image after decision fusion for 400, 4000, 8000 samples, respectively.
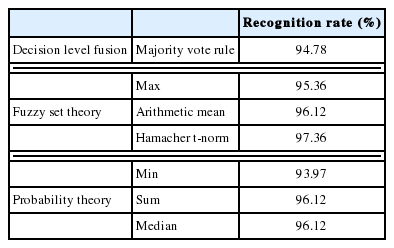
According to Table 2, the results of decision fusion show that the quality of the segmented image is improved and that the recognition rate increased by almost 5% in the case of 400 samples per class. The best rate obtained after decision fusion was 94.78% for 8000 samples per class.
Recognition rates according to training data base size using decisions fusion
Another fusion model for improving decision-making will be discussed below. It consists of combining the scores provided by the SVM classifier, as mentioned in Fig. 4, in the context of the probability theory and fuzzy logic.
Probability approach
Table 3 shows the recognition rates obtained by combining scores provided by the SVM classifier using different training database sizes and a variety of combination operators in the context of the probability theory and the result is shown in Fig. 9. We noted that the classification rates obtained by the probability approach are significantly better than the rate found by the first approach that does not use fusion.
Classification rates according to probability combination operators and data base size
(a–c) Segmented image after scores fusion by sum operator for 400, 4000, 8000 samples, respectively.
Fuzzy set theory
Table 4 shows the recognition rates that were obtained by combining scores provided by the SVM classifier using a different training database size and a variety of combination operators in the context of fuzzy logic.
Classification rates according to fuzzy logic combination operators and data base size
As seen in Fig. 10 the four textures are well discriminated compared to the decisions fusion model. The best rate obtained after the score fusion was 97.36% for 8,000 samples per class using the Hamacher t-norm.
(a–c) Segmented image after scores fusion by Hamacher t-norm operator for 400, 4000, 8000 samples, respectively.
As shown in Table 5, we observed that both the score level and decision level fusion increased recognition rate, but fusion at the score level provided a better performance.
Classification rates of fusion models
The implementation of the algorithm was performed on a computer with 2GB (RAM), 1.6GHz of CPU, and a 256×256 image. Table 6 shows the execution time of the algorithm for the decision fusion and score fusion. The fuzzy set theory is time-consuming compared to majority voting and probability approaches, but it allows for the best performance in the context of this application.
Execution time of the proposed approach
A comparison of the performance of the proposed method in the decision level fusion on other features and classifiers is described in Table 7.
Performance of the proposed decision level fusion method on other combination of feature/classifier
As seen in Table 7, the proposed algorithm increased the classification rate, even if we used other features and classifiers. Note that the recognition rates obtained by using the SVM classifier and DWT are better than the rates found by the other combinations. Also note that the fusion based on the decision level is significantly better than the method that does not use fusion for post-classification.
In order to demonstrate the validity of the proposed algorithm, experiments were performed on a remote sensing image (cf. Fig. 11). This is an IKONOS (http://www.crisp.nus.edu.sg/~research/tutorial/opt_int.htm) 1-m resolution pan-sharpened color image of an oil palm plantation. The image is 300 m across. The image is composed of three parts that can be identified from the image texture. The triangular patch in the bottom left corner is the oil palm plantation with mature palm trees and individual trees can be seen. The predominant texture is the regular pattern formed by the tops of the tree. Near the top of the image, the trees are closer together, and the tree canopies merge together, forming another distinctive textural pattern. In the bottom right corner, the color is more homogeneous, indicating that it is probably an open field with short grass. Unfortunately, exact class maps were not available.
(a) IKONOS image. (b–d) Segmented image by SVM classifier, by decisions fusion, by scores fusion respectively for 100 samples. SVM=support vector machine.
As seen in Fig. 11, the three parts can be well defined after the data fusion process. The result of the DWT and SVM classifiers contain the sur-segmentation of regions, but after applying both the decision and score fusion process the result of classification is improved, especially in the case of the decision fusion process, which clearly identifies the three regions.
Table 8 represents the results obtained by other works versus the contribution of our study. The results of our contribution show that it is possible to achieve a good fusion performance by carefully choosing the best fusion technique. For the textured image from the Brodatz album, the accuracy rate sis 97.36% for 2000 samples per class in the training step.
Comparative analysis of textured image classification
5. Conclusions
In this paper, we have proposed a novel approach for the segmentation of textured images based on information fusion. The first step was extracting the features using a Discrete Wavelet Transform that is sent to the Support Vector Machine classifier for initial labeling. Then, we proposed both a score and decision level fusion of the classification results to improve the segmentation result.
We studied an approach based on majority voting, which is an approach that uses a probability theory and a fuzzy set theory approach. This provided a significant improvement for the results of the classification of textured images. The algorithm was tested on a variety of images and showed satisfactory segmentation performance.
As for future work, we want to validate our approach against noisy textured images, and we also want to study other advanced combination schemes, such as the belief theory and naive Bayes.
References
Biography
Chaimae Anibou
She was born in Rabat, Morocco, in 1988. She received the Master degree in 2011 in Computer Science and Telecommunication from the Faculty of Science of Rabat, Morocco. She is currently a Ph.D. candidate in the Department of Computer Science & Telecommunication at Faculty of Science, University Mohammed V, Rabat, Morocco. Her research interests include Pattern recognition, image and signal processing, Information fusion.
Mohammed Nabil Sadi
He was born in Rabat, Morocco, in 1984. He received his Ph.D. degrees in computer science from the University Mohamed V, Rabat, Morocco, and also from the University of Bretagne Occidental, Brest, France, in 2010. In 2009, he joined the Department of computer science, Jean Perrin Faculty, Artois University, as a Temporary Professor. Since November 2011, he has been with the Department of Computer science, National Institute of Statistics and Applied Economics, Rabat, Morocco, where he is actually an Assistant Professor. His current research interests include Data mining, Information fusion, Pattern recognition, image and signal processing and radio cognitive. Since 2011, he is a member of IEEE signal processing Moroccan Chapter.
Driss Aboutajdine
He received the Doctorat de 3′ Cycle and the Doctorat d’Etat-es-Sciences degrees in signal processing from the Mohammed V-Agdal University, Rabat, Morocco, in 1980 and 1985, respectively. He joined Mohammed V-Agdal University, Rabat, Morocco, in 1978, first as an assistant professor, then as an associate professor in 1985, and full Professor since 1990, where he is teaching, Signal/image Processing and Communications. Over 30 years, he developed research activities covering various topics of signal and image processing, wireless communication and pattern recognition which allow him to publish over 300 journal papers and conference communications. He is presently by far the most highly published author in the fields of “Engineering and Computer science” in Maghreb countries and the second in Morocco inclusive all fields as assessed by Scopus database. He is actually director of the National Center of Scientific and Technical Research CNRST-Morocco.
